立方型钙钛矿KMgF3晶体的弹性及热力学性质
陈善俊 (长江大学物理与光电工程学院,湖北 荆州 434023;厦门大学化学化工学院,福建 厦门 361005)
金振航,张伟斌,李松,卢崇远,赵杰 (长江大学物理与光电工程学院,湖北 荆州 434023)
作为一种典型的钙钛矿型氟化物,KMgF3具有良好的光学均匀性、较高的透过率、热稳定性及高能辐照下的交叉发光性能[1],在窗口材料、闪烁材料及可调激光材料等领域具有重要应用前景,因此得到广泛关注。试验方面,Komar等[2]通过Bridgman方法在真空条件下生长了纯KMgF3单晶体;Darabont等[3]通过Czochralski和Bridgman 2种方法在氮气的气氛下生长了KMgF3单晶,并用单晶X射线衍射方法测定其晶格常数为3.978nm;臧春雨等[4]采用Bridgman方法在真空和氩气的气氛下分别生长了KMgF3单晶,并研究不同的条件下晶体的生长质量;Wood等[5]利用高分辨中子粉末衍射谱仪(HRPD)研究了4.2K、298K温度下及373~1223K温度范围KMgF3的晶体结构,研究发现该材料在所有温度下均保持立方结构;Vaitheswaran等[6]使用同步辐射源X射线衍射技术进行了原位高压粉末试验,发现立方结构KMgF3晶体在40GPa以下压力范围能稳定存在;Aguado等[7]发现KMgF3的立方钙钛矿结构在50GPa以内压力范围依然稳定存在;Wu等[8]通过非等价取代方法研究了Yb3+/Er3+共掺杂的KMgF3纳米晶的转换发光特性。
理论方面,Nishimatsu等[9]采用第一性原理研究了掺杂V, Cr, Mn, Fe, Co和Ni等3d过渡金属对KMgF3晶体的能态密度的影响;Sahnouna等[10]采用全势线性缀加平面波(FPLAPW)方法,研究了30GPa压强下的几何结构、电子和光学性质,电子结构对高静压力的依赖性显示出线性行为;程芳等[11]采用第一性原理研究了零温零压下KMgF3晶体的光学性质;Cui等[12]采用第一性原理研究了高压下的KMgF3晶体的电子及光学性质,在100GPa的压强范围内,该材料为间接带隙绝缘体;Vinit等[13]采用第一性原理研究了零温零压下KMgF3晶体的电子结构、弹性及介电性质;Sahl等[14]也采用第一性原理研究了0~10GPa压强范围内KMgF3、K0.5Na0.5MgF3和NaMgF3晶体的结构、电子、弹性及光学性质;Syrotyuk等[15]采用GW方法研究了钙钛矿KMgF3晶体的电子态密度及光学性质;Sousa等[16]采用经典的原子模拟方法研究了50GPa内AMgF3(A=K, Rb, and Cs)晶体的结构及机械性质,压强约为2GPa时,KMgF3和RbMgF3由脆性向延展性转变。
综上,国内外科研工作者对KMgF3晶体的电子结构及光学性质研究很丰富,但对其弹性和热力学性质等研究较少,特别是高温高压下KMgF3晶体的热力学性质研究较少。目前,几乎不依赖任何经验参数的第一性原理方法,已经广泛应用于材料的结构设计和性能计算中[17~22]。一方面,它能够辅助和解释试验现象,另一方面,能较好地预测材料的性质,为新材料的试验研究提供理论指导。为此,笔者运用第一性原理赝势平面波密度泛函理论[23],研究高压下立方钙钛矿结构KMgF3晶体的弹性及热力学性质,为其在极端条件下进一步的应用研究提供理论指导。
1 理论模型和计算方法
1.1 理论模型
KMgF3晶体为立方钙钛矿结构,其空间群为Pm-3m。每个KMgF3晶胞中含有5个原子,Mg原子占据晶胞的体心,而K原子位于8个顶角位置,F原子占据晶胞的面心,各个原子的坐标分别为K(0,0,0),Mg(0.5,0.5,0.5),F(0.5,0.5,0),其原子空间排布如图1所示。
1.2 计算方法
计算基于密度泛函理论(DFT)[24]的CASTEP[25]程序完成。采用BFGS算法[26]对晶胞进行几何结构优化。电子交换关联函数、原子势分别选用GGA-PBEsol[27]和超软赝势(ultrasoft pseudopotential);平面波的截断能Ecut取650eV,布里渊区k点网格选取12×12×12。在迭代过程中,能量自洽收敛条件设为5×10-6eV/atom、最大力收敛标准取为0.01eV/Å,最大位移收敛标准为5×10-4Å。
2 结果和讨论
2.1 几何结构优化
表1列出了零温零压下KMgF3计算得到的晶格常数及其他理论值与试验值。对比表1中数据可以看到,笔者计算得到的平衡晶格常数为4.009Å,仅比试验值(4.006Å)[6]大0.075%,比其他的理论值[10,12~14]更符合试验值。因此,笔者所采取的计算方法是可行的,该优化结果对其性质进行讨论是可靠的。

表1 零温零压下KMgF3的晶格常数
2.2 弹性性质
弹性性质[28]在物理学、化学、材料科学等领域是一个极其重要的研究对象。晶体的一些固态性质如比热容、熔点、状态方程等都受弹性性质影响。根据弹性常数,可以获得晶体结构的延展性和各向异性等信息。
KMgF3是面心立方结构晶体,对于立方晶体,弹性常数Cij只有3个非零独立分量,即C11、C12、C44。根据Voigt近似[29]:
(1)
根据Reuss近似[30]:
(2)
对于多晶体模量,Hill[31]从理论角度证明了剪切模量G为GV和GR的算术平均值,即:
(3)
在零压的条件下,立方晶体的体弹模量B与弹性常数满足关系式:
(4)
表2给出了零温零压下KMgF3晶体的弹性常数、体弹模量B和剪切模量G。从表2可以看出,笔者所计算晶体弹性常数(C11,C12,C44)及体弹模量B与试验值[32]及其他的理论计算值均符合。这进一步可以说明笔者采用的计算方法是可行的,用该方法计算的结果是可靠的。

表2 零温零压下KMgF3晶体的弹性常数Cij、体弹模量B和剪切模量G
根据立方晶体的结构稳定性条件[33]可知,弹性常数Cij的各个独立分量需同时满足以下3个条件:
(5)
由于C11>B>C12,上面不等式中的各物理量满足以下关系:
(6)
(7)
表3给出了0~120GPa压强范围内KMgF3晶体计算得到的弹性常数(C11,C12和C44),以及相应的体弹模量B,图2为0~120GPa压强范围内弹性常数、体弹模量与压强的曲线图。
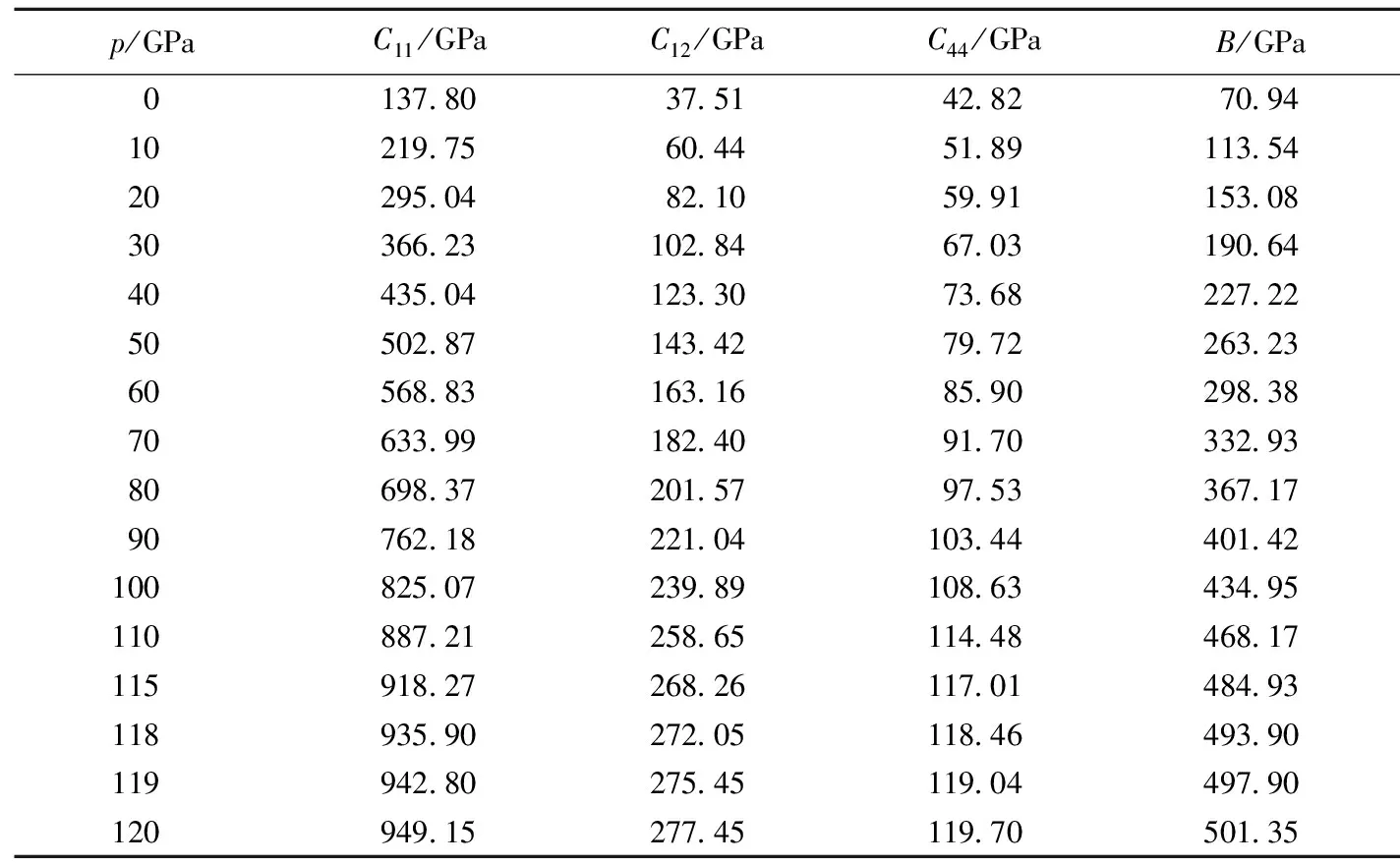
表3 零温时不同压强下钙钛矿结构KMgF3的弹性常数Cij与体弹模量B
结合表3数据和图2曲线可以看到,当压强增大时,弹性常数(C11,C12和C44)以及体弹模量B都会随之增大,其中C11相比于C44、C12增加幅度更大,这是因为C12和C44对压强的敏感性不如C11。
把表3中的数据代入式(6)计算可知,当p<119GPa时,计算结果满足立方晶体的结构稳定性条件,说明此时KMgF3晶体的结构是稳定的;而当p>119GPa时,所计算结果与立方晶体对结构稳定性的要求不完全一致,这意味着此时的KMgF3晶体的结构是不稳定的。如果压强继续变大,会有相变的可能性。因此,KMgF3在119GPa压强内是稳定的,故推测KMgF3晶体的相变点是119GPa,目前并没有相关的试验值及理论值进行对比。
依据文献[33]Pugh提出的晶体力学行为的标准,高的B/G值表明晶体有更好的延展性,反之是易碎的,其临界值为1.75。由表3数据及式(1)~(4)可得KMgF3的B/G值为1.554,这表明KMgF3晶体延展性稍微差一些,说明低压下制备比较困难。通过表3的数据计算不同压强下的B/G值,可以发现KMgF3晶体的B/G值在相变范围内随着压强的增加而增大,这同样表明了KMgF3晶体易在高压条件下制备。
2.3 热力学性质
物体的热力学性质是指物质处于平衡状态下压强p、体积V、温度T以及其他的热力学函数之间的变化规律。研究在不同外加压强和温度作用下,KMgF3晶体结构及热力学性质的变化规律是有必要的。首先,以零温零压下的晶格常数为标准,选取一系列的晶格常数,分别计算相应的原胞体积V和总能量E,然后把能量和体积用Birch-Murnaghan equation of state(EOS)状态方程[34]进行拟合,拟合得到E-V曲线如图3所示。
根据之前预测的KMgF3晶体的相变压强为119GPa,笔者将研究KMgF3晶体在0~120GPa的压强下的热力学性质,同时根据文献报道,高温下(1223K时)KMgF3的立方型晶体结构保持不变,故笔者将研究1200K温度范围内的热力学的性质。结合图3中E-V曲线的数据,利用GIBBS程序[35]完成KMgF3晶体的相关的热力学性质计算。
图4给出了T=0、400、800、1200K这4个温度时KMgF3晶体相对体积V/V0与压强p的关系曲线(其中V0为p=0GPa时晶体平衡体积)。由图4可知,在温度一定的情况下,该晶体的相对体积随着压强的增大而减小;在压强一定的情况下,相对体积随温度升高而减小,这是因为温度升高,热运动加剧,从而使固体较容易被压缩导致的。
图5和图6分别为p=0、40、80、120GPa这4个压强时KMgF3晶体等体热容Cv及等压热容Cp与温度T的关系曲线。由图5和图6可知,当温度T相同时,等体热容和等压热容均随压强增大而减小;在压强相同的条件下,等体热容和等压热容均随压强增大而增大,当温度T<500K时,Cv随着温度的逐渐升高幅度明显,这是由于在此范围内其体积变化较明显导致的;而当温度T>500K时,随着温度的继续增加,等体热容变化很小,这是因为存在晶体非谐效应(高阶项)的作用效果,在高温条件的作用下,Cv随着温度的进一步升高会无限接近Dulong-Petit极限,其值为3nNAkb(NA为阿伏伽德罗常数、n为每个原胞包含的原子数,kb为玻尔兹曼常量);而对于KMgF3,n=5,则Dulong-Petit极限值约为124.75J/(mol·K)。
图7给出了压强p=40、80、120GPa时KMgF3晶体热膨胀系数与温度的关系曲线。由图7可知,当压强相同时,随着温度的逐渐增大,其热膨胀系数先迅速增大,随后趋于某条渐近线,这表明KMgF3晶体在高温下发生了明显的体积膨胀现象。同时可以发现,在温度T相同的条件下,热膨胀系数随压强的增大而减小,这说明KMgF3晶体在高压条件下,具有良好的体积不变性。
图8为KMgF3的晶体的相对德拜温度和相对热容与压强的关系。由图8可知,当压强保持不变的情况下,随着温度的升高,相对德拜温度也随之升高,相对热容越大;当温度保持定值不变时,KMgF3晶体的相对德拜温度随压强升高而增大,但是KMgF3晶体的相对热容随着压强增大而减小。通过准谐德拜模型,笔者计算得到常温(T=300K)下,KMgF3晶体的德拜温度Θ为485.85K。德拜温度大于对应的温度,这意味着KMgF3的热容不遵循经典规律,即热容不是定值,这与图5和图6的结论是一致的。
3 结论
1)基于第一性原理平面波赝势密度泛函理论,并结合准谐德拜模型,研究了零温零压和高温高压条件下立方型钙钛矿KMgF3晶体的弹性及热力学性质。计算得到的KMgF3晶体的晶格常数、弹性常数、体弹模量、剪切模量与试验值及其他理论值都符合得很好。计算得到KMgF3的B/G值为1.554(小于1.75),表明KMgF3晶体延展性差。
2)依据立方晶体力学稳定条件,首次得到KMgF3晶体的相变点约为119GPa。通过准谐德拜模型,得到晶体在常温条件下德拜温度Θ为485.85K。热容随压强升高而降低,在高温下等体热容接近于Dulong-Petit极限。
3)相关研究结果可以为KMgF3晶体在高温高压下的热力学方面的应用提供理论支持。

