基于最速曲线的投资组合调整方法
李宗欣, 陈志平, 王美花
(1.西安交通大学 数学与统计学院,陕西 西安710049;2.西北大学 经济管理学院,陕西 西安710127;3.西安电子科技大学经济与管理学院,陕西 西安710071)
0 引言
在开始一项投资活动时,投资者通常会预先设定到期日和相应的目标收益率,如用一年的时间实现百分之二十的收益率。这一事宜可以利用Markowitz[1]的原创性工作(均值方差理论)进行建模。该理论在限定预期收益的基础上极小化投资风险,或者在控制投资风险的前提下极大化期望收益。截止到目前,这种投资组合优化问题已经从多个角度得到扩展,如鲁棒投资组合优化问题[2,3]、多期投资组合调整模型[4,5]以及行为投资组合选择模型[6,7]。
最近,投资组合调整问题受到越来越多的关注。这主要是因为投资者倾向于根据新信息去不断地调整他们的投资组合。这种倾向性在投资期限比较长的情形下愈加明显。总的来说,投资组合调整模型分为两类:(1)连续时间情形[8,9];(2)离散时间情形[10,11]。特别地,Das等[12]指出,通过离散时间地调整投资组合,投资者就可以获得显著的收益。对于任意给定的投资期限,他们还计算出了最优调整频率的计算方法。正因为此,本文考虑周期性地对投资组合进行调整。
注意到,已有离散情形下的投资组合调整模型似乎很少考虑投资者在实际投资过程中的心理因素及其变化过程,更多详情请参见De Lara和Leclere[13]。因为资金的时间价值在金融活动中扮演着十分重要的角色,所以我们不能忽略它,尤其是当投资期限较长时。具体地,当开展一项中长期投资活动时,投资者希望能尽快达到预设的目标收益率。这一方面是因为早达到目标可以在剩余的时间里额外获得固定收益,另一方面是因为早达到目标可以避免由未来的不确定性带来的风险。因为数学中的最速曲线描绘了从一点到另一点的最快路径,所以投资者这种所谓的“最短时间”心理可以借助该曲线进行建模。因此,本文的目标是基于最速曲线建立一个新的投资组合调整模型,以便能够帮助投资者尽可能快地实现他们的目标。
本文的结构如下。第一节基于最速曲线建立了目标财富的动态方程。第二节进一步提出了一个新的投资组合调整方法并探讨其具体求解步骤。第三节分别对取自德国股票市场的四个典型数据集和中国股票市场的真实数据进行实证研究。第四节总结全文。
1 最速曲线与目标财富动态方程
在构建新的投资组合调整模型之前,我们在本小节基于最速曲线构建目标财富的动态方程。假设投资者在初始时刻拥有财富W1,他希望在T时刻拥有财富WT。不失一般性,我们考虑n个风险资产作为投资对象。为了方便表述,我们将下文可能出现的所有记号汇总如下:μt=(μt1,…,μtm)T:在t∈[1,T)时刻决策时的期望收益率向量;
Σt:n个风险资产在t时刻决策时的协方差矩阵;Wt:在t时刻决策时实际拥有的财富;ut=(ut1,…,utn)T:在t时刻决策得到的最优投资组合;Dt:在t时刻决策时的目标财富;Rt:在t时刻决策时的目标收益率(相对于W1);Ot:在t时刻决策后与紧接下一次决策前实现的收益率向量;e:n维全1列向量。
1.1 最速曲线
最速路线是从一个点到另外一个点的最优路径,这种最优是指耗费的时间最短。该曲线可以借助变分分析和最优控制求解得到。数学上,最速曲线满足如下微分方程

这里D是一个正的常数。相应的参数方程可以表示为

这里θ∈[0,π]是一个参数,L是一个取值为正的常数。
截止到目前,最速曲线在自然科学中有着十分重要的应用。如Babb and Currie[14]已将其成功应用到物理问题中去。在本文中,我们试图将其应用到社会科学中。具体地,为了帮助投资者尽快实现他们的目标,我们基于最速曲线提出一个新的投资组合调整方法。为此,我们首先借助最优曲线构建目标财富的动态方程。
1.2 目标财富的动态方程
正如我们在引言中所说,投资者无一例外地希望尽快实现他们的目标。因此,投资者目标财富Dt的动态方程可以表述为
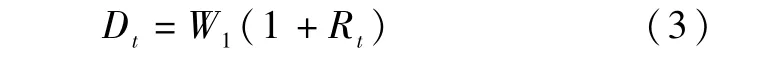
这里Rt满足最速曲线方程,即

关于目标财富的动态方程,式(3)和式(4),我们给出如下三点说明。
注1式(4)中的取值可由W1,WT,T确定。具体地,因为点(T)落在该曲线上,所以代入式(4)即可获得L的取值。
注2式(3)和式(4)给出了目标财富的动态变化过程,这有助于投资者在投资期限内实时地调整投资策略。
注3式(3)和(4)可以反映著名的时间效应。具体地,因为θ∈[0,π],所以

式(5)意味着随着时间的流逝,目标财富应该积累的越来越多。式(6)进一步说明了财富积累的速度越来越慢。即随着到期日的来临,投资者在每次策略调整时的目标收益逐渐下降。因为收益越低风险越小,所以递减的目标收益意味着投资者愿意承受的风险越来越小。换句话说,随着到期日的来临,投资者变得越来越保守(风险厌恶程度越来越高)。这正是Shi等[6]提到的时间效应现象。
2 基于最速曲线的投资组合调整模型及求解
基于前述目标财富的动态方程,式(3)和式(4),我们在本节构造投资组合调整模型并给出该模型的具体求解步骤。
2.1 基于最速曲线的投资组合调整模型
正如在引言中所说,我们考虑周期性地调整投资策略。假设投资者想在整个投资期限内做次决策,则k(k=1,…,K)第次决策发生的时间为

首先,我们考虑第k次决策时实际可用的财富Wtk。假设投资是自融资的,即投资者在整个投资期限内不额外地注入资金,则Wtk等于Wtk-1加上第k-1次决策实际获得的收益。即
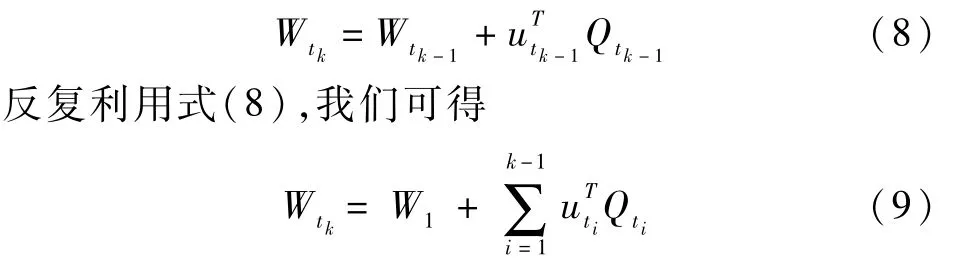
因此第k次决策得到的最优投资组合utk受到如下限制

这里Wtk可以由式(8)或者式(9)确定。
其次,我们考虑确定第k个最优投资组合utk时的目标财富约束。为了尽快达到预设的终期财富,我们利用最速曲线实时地控制目标财富的动态,因此我们有

最后,我们讨论上述公式的含义。从式(9)中不难发现,在进行第k次投资决策时可用的财富与之前的决策和实际的样本外表现息息相关。由于股票市场的波动是随机的,故实际的财富过程与目标财富动态不一致这种情形是难免的。不失一般性,我们假设Wtk<Dtk-1。根据式(11),第k次调整决策时的真正任务是获得收益Dtk-Wtk而不是Dtk-Dtk-1。显然,Dtk-Wtk>Dtk-Dtk-1。换句话说,如果前面的投资被证实是失败的,即没有达到预设的目标,则投资者会在第k次决策时设定一个更高的目标收益。因为收益越高风险越大,所以增加的目标收益意味着投资者愿意承受更大的风险。相反地,如果前面的投资被证实是成功的,即超额完成了预设的目标,则投资者在第k次决策时会变得风险厌恶,即不愿意承受很大的风险。这恰好刻画了实际投资活动中普遍存在的处置效应现象。该现象有时也被称为承诺升级效应[15]。
在进行每一次投资组合调整决策时,投资者都希望在达到目标财富的基础上去极小化投资风险[1]。在本文中,我们选取最经典的方差作为风险度量。记第k次投资组合调整问题为(Ptk),则第k次投资决策可以通过求解如下模型得到

值得注意的是,模型(Ptk)只有在条件Wtk(1+max{μtk})≥Dtk满足的前提下才可行。该不等式意味着如果将所有财富投资到期望收益率最高的资产上,那么我们可以实现预设的目标财富。为了确保投资组合调整能够持续进行,我们需要处理一些极端情况。受前述处置效应的启发,如果之前的投资被证实是失败的,且Wtk(1+max{μtk})<Dtk,则我们将所有财富投资到期望收益率最大的资产上。相反地,如果我们提前完成了预设的终期目标,则我们将所有财富投资到方差最小的资产上。经过这些处理,基于最速曲线的投资组合调整模型可以汇总如下:
情形1若Wtk(1+max{μtk})<Dtk,则令

其中p∈{1,…,n}由Σtk(p,p)=Σtk(j,j)确定。
情形3对于其它情形,utk可以通过求解凸二次规划问题(Ptk)获得。
2.2 模型求解步骤
上文基于最速曲线构建了投资组合调整模型,为了方便其在实际中的应用,我们进一步探讨该模型的求解,具体步骤如下:
Step 1参数设置:初始财富W1,投资期限T,目标终期财富WT,决策次数K;
Step 2将点(T,)代入(4)式,求得L,从而确定目标财富的动态方程;
Step 3按照(7)式计算出K次决策发生的时间t1,t2,…,tK;
Step 4根据(12)式分别计算出K次决策时的目标财富Dt1,Dt2,…,DtK;
Step 5对于k=1,…,K,按照(9)式计算出第k次决策时实际拥有的财富Wtk,特别地,Wt1=W1。
若Wtk(1+max{μtk})<Dtk,则第k次决策得到的最优投资组合utk由(13)式确定;
若Wtk≥WT,则第k次决策得到的最优投资组合utk由(14)式确定;
Step 6令k=k+1,转Step5。
3 实证研究
本节对前述基于最速曲线的投资组合调整模型进行实证研究。为了说明新提出的投资组合选择方法的实用性和有效性,我们采用成熟市场—德国股票市场的多个数据集进行实证测试。
3.1 数据集与性能指标
本文的实证研究基于德国股票市场(欧洲最大的股票市场)的历史数据进行。为了充分利用分散化效应,我们选取100只股票作为研究对象。具体地,首先考虑2005年4月1日当天XETRADAX100指数的100个成分股,然后剔除在考虑的时间区域内有连续5天停牌或者累计超过30天数据缺失的股票,最后从德国股票交易市场中按照字母顺序选取成分股以外的其余股票以填补被剔除股票留下的空缺。
为了充分说明新投资组合调整模型的实用性和有效性,我们考虑所有可能的市场趋势,即选取四种不同类型的数据集进行实证测试。具体地,第一个数据集的特征是指数在样本内和样本外均呈上涨趋势(简记为up-up);第二个数据集的特征是指数在样本内呈上涨趋势,但是在样本外呈下跌趋势(简记为up-down);第三个数据集的特征是指数在样本内呈下跌趋势,但是在样本外呈上涨趋势(简记为down-up);第四个数据集的特征是指数在样本内和样本外均呈下跌趋势(down-down)。详细的股票代码、四个数据集的起止日信息以及相应的收益率数据可以参考Guastaroba等[16]和王等[10]。值得一提的是,对于每一个数据集,我们将前200个日收益率视为样本内数据,并在接下来的60个交易日进行投资组合调整。
在本文中,我们还考虑了其它两种投资组合选择方法用于实证比较。一是购买并持有策略(N-RS),即在投资开始时做出投资决策并一直保持该决策不变,直到投资活动结束。二是平均分配目标收益策略(A-RS),即将整体的投资目标平均分配到每一次调整中。为了方便描述,我们将新方法导出的最优投资策略称为基于最速曲线的策略(B-RS)。
为了全面评估不同投资组合选择模型导出的最优投资组合在样本外的表现,我们从多个角度对它们的表现进行对比。首先,我们判断这些投资组合调整方法是否可以成功地在到期日来临时实现预设的目标。对于能够成功完成任务的投资组合调整方法,我们进一步比较首次达到预设目标的时间(首达时),这与达到目标需要的最小调整次数(k*)一一对应。显然,k*越小,首次达到预设目标的时间越早,从而相应投资组合选择方法的性能越好。更进一步地,我们给出在首达时刻实际拥有的实际财富(Wtk*)。显然,Wtk*越大,相应投资组合选择方法的表现越好。
以下所有实证测试都在联想个人电脑上完成。电脑的参数是Core(TM)i5-2400,CPU 3.10GHz,Memory 4.00GB。我们利用MATLAB(R2009a)估计协方差矩阵Σt和期望收益μt,并利用MATLAB工具包中的经典且有效的求解器(Quadprog)去计算最优投资策略。
3.2 实证结果与分析
在本次实验中,我们取W1=10000,WT=11000且K=10。针对四个不同的数据集,我们分别求解相应的投资组合调整模型。不同投资组合选择模型导出 的最优投资组合在样本外的实证结果如表1所示。

表1 不同投资组合调整方法在不同数据集下的实证结果
首先,从表1中不难看出,在考虑的三个投资组合调整方法中,购买并持有策略(N-RS)表现最差。这是因为它在四种不同的市场趋势下均未成功地达到预设的目标。造成这种现象的原因也很容易解释。随着时间的流逝,市场在不断地发生变化,原本选择出来的优良股票可能会在一段时间后表现变差。因为购买并持有策略在整个投资期限内都保持投资组合不变,所以它并不能及时地出售变差的股票以如期实现预设的目标。N-RS策略在样本外的不良表现再次证实了投资组合调整的必要性。
其次,综合比较策略A-RS与B-RS对应的首达时和实际财富可以发现,新提出的基于最速曲线的投资组合调整方法在up-down,down-up与downdown三个数据集下都表现出显著的优越性。具体地,在up-down和down-up两个数据集下,新方法不仅能够更快地达到预设的目标,而且能够在较少的时间内获得更多的财富。在市场持续下跌(down-down)情形下,虽然两种投资组合调整方法同时达到了预设的目标,但是新方法对应的财富(11356)却比常用的平均分配目标方法对应的实际财富(11151)大得多。新投资组合调整方法在样本外表现出的这些优越性可归功于最速曲线的应用。该曲线不仅给出了能够帮助投资者尽快实现预设目标的最优路径,而且刻画了在实际投资过程中普遍存在的时间效应和处置效应现象,从而可以帮助投资者不断根据市场中涌现的新信息去调整持有的投资组合。
最后,基于最速曲线的投资组合调整方法的优越性在市场持续上涨(up-up)情形下不复存在。更糟的是新方法甚至不能像常用的平均分配目标方法那样在投资到期日成功地实现预定的目标。这一结果也很容易解释。根据前述关于新投资组合调整模型的讨论,我们的新方法会在经历一次失败后将所有的钱投到过去表现最好的那只股票中去。然而,up-up型数据集意味着市场处于牛市,牛市的主要特征是板块轮动,因此过去表现最好的那只股票会在接下来的时间变得逊色,从而我们的投资组合调整策略不再能及时地捕捉到投资机会,这直接导致投资者无法在到期日实现预设的投资目标。
由以上讨论可知,新提出的基于最速曲线的投资组合调整模型在大多数市场趋势下都颇有良效。为了进一步展示新方法在up-down,down-up和down-down三种市场趋势下凸显出的优越性,我们考虑截止到首达时刻不同投资组合调整策略下实际财富的变化过程。详细结果如图1~3所示。

图1 不同投资组合调整方法在up-down数据集下的实际财富过程

图2 不同投资组合调整方法在down-up数据集下的实际财富过程
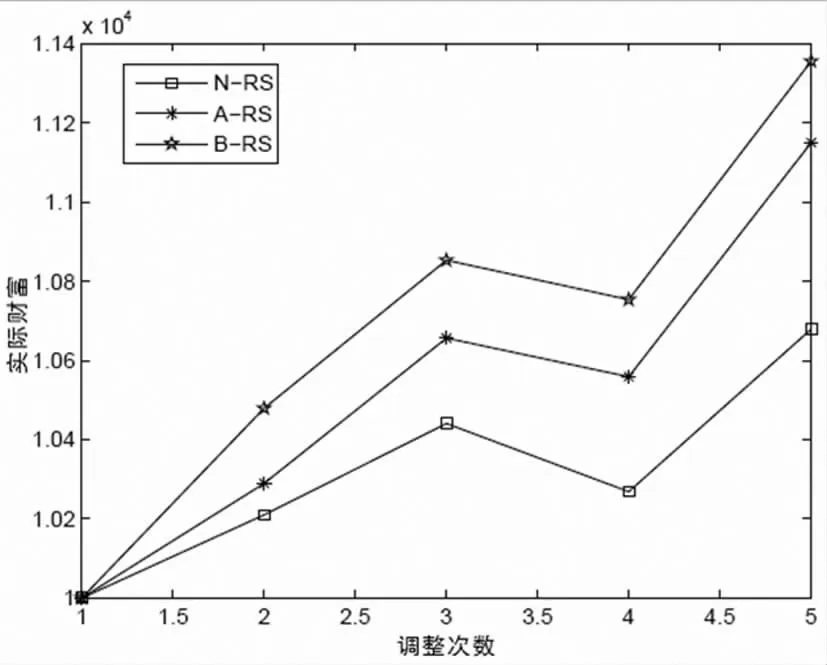
图3 不同投资组合调整方法在down-down数据集下的实际财富过程
从图1~3中可以看出,基于最速曲线的投资组合调整模型导出的B-RS策略对应的实际财富过程曲线总是位于最上方。即在达到预设目标之前,我们的新方法也总能比其它两种方法获得更多的实际财富。这意味当投资者因为某些特殊原因不得不提前终止投资活动时,我们的新方法总能获得更多的收益。
综上所述,在大多数市场趋势下,本文新提出的基于最速曲线的投资组合调整模型不仅可以帮助投资者尽快实现预先设定的投资目标,而且可以在较少的时间里获得更多的财富。更为重要的是,当投资者因为某些特殊原因不得不终止投资活动时,我们的新模型总能获得最多的收益。
为了进一步测试新方法的鲁棒性,我们变化,以及K的取值并按照上述思路进行实证研究,所得T,WT结果与表1,图1~3十分相似。鉴于空间限制,我们在本文中省略这些实证结果。此外,为了测试新方法在新兴市场中的表现,我们采用中国股票市场的数据进行实证研究。类似于德国股票市场的数据选取方法,我们考虑2017年9月8日当天上证50指数的50个成分股,剔除在考虑的时间区域内(2017年2月6日至2017年9月8日)有连续5天停牌或者累计超过30天数据缺失的股票,然后从上海证券交易所中按照股票代码顺序选取成分股以外的其余股票以填补被剔除股票留下的空缺。我们将前100个日收益率视为样本内数据,并在接下来的50个交易日进行5次决策。实证结果表明,新方法不仅能够更快地达到预设的目标,而且能够在较少的时间内获得更多的财富。具体地,购买并持有策略(N-RS)和平均分配目标收益策略(A-RS)经历5次调整仍未达到预设的终期目标财富,而基于最速曲线的策略(B-RS)在4次决策后即超额完成预设的目标(财富值高达11258)。不同投资组合调整策略下实际的财富变化过程如图4所示。

图4 不同投资组合调整方法在中国股票市场中的实际财富过程
4 结论
为了帮助投资者尽快实现他们的目标,我们在本文中基于著名的最速曲线提出了一个新的投资组合调整方法。该方法可以反映两个著名的投资现象——时间效应和处置效应。为了说明新提出的投资组合调整模型的实用性和有效性,我们利用来自德国股票市场的四个描述不同市场趋势的数据集展开了一系列的实证研究。样本外结果再次证实了投资组合调整的必要性。更为重要的是,实证结果表明在大多数市场趋势下,新提出的投资组合调整方法不仅可以帮助投资者尽快实现预先设定的投资目标,而且可以在较少的时间里获得更多的财富。更为重要的是,在成熟市场中,当投资者因为某些特殊原因不得不终止投资活动时,我们的新模型总能获得最多的收益。

