干散货运价波动的杠杆效应特征研究
——基于非对称随机波动模型
李电生, 聂福海
(1.中国海洋大学 经济学院,山东 青岛266100;2.中国海洋大学 海洋发展研究院,山东 青岛266100;3.哈尔滨工业大学(深圳)经济管理学院,深圳518055)
0 引言
作为国际干散货航运市场走势的晴雨表,以BDI为代表的波罗的海系列运价指数能较为完全地反映大宗商品海洋运输市场的即期信息。受全球经济景气荣枯、原材料行情变化和自然灾害等因素影响,加之新造船交付时间滞后性的冲击,干散货航运市场存在很大的不确定性风险,并通过运价指数的波动性特征表现出来。近年来,在FFA(远期运费协议)市场中海运金融衍生品交易量不断扩大,深刻改变了干散货运价的定价模式,加上干散货航运市场中国际投机资本和被放大的中国因素共同影响,干散货运价指数一定时期内脱离其基本面的支撑。特别是2008年经济危机前后,BDI经历了“过山车”式的剧变,在2008年5月攀升至11793点的历史高位后在2015年下半年一度在300点左右徘徊,其间剧烈波动、几经反复,为国际干散货航运市场主体带来巨大的风险。
以BDI为代表的干散货运价指数的波动性特征越来越受到国内外学者重视,Xu等[1]引入ARCH类模型验证了干散货运价指数波动的集聚性特征,且船型越大则其分船型运价指数的波动程度越剧烈。Gong等[2]利用长记忆的随机波动模型对分船型运价指数BPI和BCI实证研究,验证了干散货运价指数的波动具有长记忆性特征。王磊等[3]运用谱分析方法研究BDI日数据和月度数据的周期特征,得出干散货运价指数具有周期波动特征的结论。Timotheos等[4]研究发现运价指数的频繁波动是干散货航运市场的重要特征,这种波动特性是干散货航运市场风险的主要来源。由此可见,国内外学者对干散货运价指数波动性的研究主要集中在其波动集聚性、尖峰厚尾及长记忆性等特征,而对另一典型特征——波动的非对称特征研究较少。
由信息冲击引起的资产价格变化,会对资产价格预期波动率造成非对称影响,当资产价格收益与预期波动成负相关关系,即同等强度的利空消息要比利好消息引起更大的市场波动,这时称为杠杆效应,反之为反杠杆效应。杠杆效应最早是由Black[5]提出,并解释为由于股票价格下跌导致企业资产负债比率增加,从而引起持股风险和和市场波动的增加。Vo等[6]以SV类模型(随机波动模型)实证分析了在许多国家的股票市场存在杠杆效应。Jacquier等[7]、Nomikos等[8]、Gil-Alana等[9]将 杠 杆效应的研究对象由股票市场分别扩展到汇率市场、能源期货市场和有色金属期货市场,研究正向冲击和负向冲击对资产收益预期波动的非对称影响,大量实证研究表明市场波动的非对称性特征多数表现为杠杆效应,也不排除反杠杆效应的存在。
与股票、期货市场相比,干散货运价的剧烈波动将给航运实体市场带来巨大的风险,直接影响航运企业和租船人的投资和经营决策,所以研究不同信息冲击下干散货运价波动的变化规律,对航运企业、贸易商、大宗商品采购商及FFA专业投资机构具有重要理论和现实意义。近年来,Xing等[10]少数学者在研究干散货航运市场过程中对运价波动的非对称特征有所涉及,开始关注利好和利空消息对干散货航运市场波动的不同影响,但值得注意的是这些研究大多基于Nelson提出的EGARCH模型,并缺乏对干散货运价波动杠杆效应特征的合理解释。EGARCH模型和ASV模型(非对称随机波动模型)[11]是研究资产价格波动中杠杆效应特征的两种主要建模方式,ARCH类模型将资产收益率的时变方差表示为确定的自回归函数,而ASV模型将波动视为一个不可观测的随机过程,在准确性、全面性等方面具有一定优势。
近年来,干散货运价大起大落、剧烈波动,在极端风险状况下,传统的ASV模型的正态分布假定对收益率条件分布的厚尾特征考虑不足。本文建立基于student-t分布的改进ASV模型,在贝叶斯分析的基础上通过MCMC方法进行参数估计,并根据DIC信息准则对传统的ASV模型和改进的ASV模型比较。通过实证研究,得出改进的厚尾分布的ASV模型能更加准确、逼真地刻画干散货运价波动的杠杆效应特征。
1 改进的ASV模型
1.1 基于正态分布的ASV模型
在基于正态分布的ASV模型(记为ASV-N模型)中,假定随机误差项εt和ηt+1相关且服从二元正态分布。ASV-N模型的离散时间的模型形式为:

(1)式为测度方程,(2)式为波动方程。其中,yt为第t日的资产收益率;ht为不可观测的第t日收益的对数波动水平,服从参数φ的高斯AR(1)过程;μ表示波动的平均水平,τ2是对数波动率的方差,φ为波动的持续性参数,在φ∈(-1,1)时,则SV模型是协方差平稳的。
1.2 改进的student-t分布的ASV模型
在ASV-N模型中随机误差项服从二元正态分布的假设,意味着测度方程中的条件收益率服从正态分布,此时捕捉到的杠杆效应对实际市场的极端波动风险考虑不足,与实际的资产收益分布通常表现出的厚尾特征并不符合,这样会影响尾部概率估计的精度。本文将随机误差项服从二元正态分布的假设变为服从二元联合t分布为协方差矩阵,v为自由度,且v>2)。已知二元联合t分布的边际分布为一元t分布,则~tv(0,1),~tv(0,1),ρ=corr(εt,ηt+1),当v>2时,可以通过调整自由度参数v,使ASV-T模型既能适应资产收益分布的厚尾特征,又能刻画资产收益波动的杠杆效应,从而表现出更好的稳健性。
1.3 杠杆效应的原理解释
为从ASV-T模型角度解释相关系数ρ在描述波动的非对称性的原理,这里引入另一个随机变量
由多元t分布的线性变换不变性可得其均值和方差分别为:E(λt)=0,Var(λt)且λit.i.d.~tv(0,1),corr(εt,λt)=0。
在控制变量ht,μ,φ,τ2,ρ,v的前提下,加入厚尾特征的ASV-T模型的波动方程可表示为ht+1=μ+φ(ht-μ)+τλ+τρytexp(-ht/2)。
对第t+1日的条件对数波动率ht+1关于第t日的收益率yt求偏导可得。

2 模型的贝叶斯分析
2.1 贝叶斯参数估计
在ASV-T模型中,只有收益率序列y=[y1,y2,…,yn]是已知的,待估参数μ,φ,τ,ρ,v(记为未知参数向量θ)和不可观测的对数波动率序列h都是未知的,这里利用后验分布π(θ|y)对待估参数μ,φ,τ,ρ,v进行贝叶斯估计。
已知自由度为v的一元t分布的概率密度函数因此对于给定的ht,条件收益率序列yt|ht~tv(0,exp(ht)),其(1+exp(-ht)/v)-(v+1)/2。因此,模型的似然函数为待估参数μ,φ,τ,ρ,v和不可观测的对数波动率h1:n的联合先验密度函数为π(θ,h)=π(μ,φ,τ,ρ,v),π(h1|μ,τ)π(ht+1|ht,μ,φ,τ,ρ,v)。
根据贝叶斯定理,不可观测量的联合后验密度分布与联合先验密度函数和模型的似然函数之积成正比,即

2.2 MCMC随机抽样算法
直接用联合后验分布π(θ|y)估计待估参数,面临着高维积分困难的问题,且每个待估参数后验分布的解析表达式难以求得。对每个未知参数的函数g(θ)可用后验分布表示为g(θ)=∫Θg(θ)π(θ|y)dθ(θ∈Θ),g(θ)的 后 验 均 值E[g(θ)|y]可 用=
其中,θ(1),θ(2),…,θ(n)是来自后验分布π(θ|y)的容量为n的样本。如果此样本是独立的,由大数定律,样本均值依概率收敛于E[g(θ|y)]。马尔可夫链提供从后验分布π(θ|y)直接抽取的非独立的随机样本{θ(0),θ(1),θ(2),…}(即一条马氏链)仍具有良好的性质。如果样本容量n足够大,则认为样本均值是未知参数的近似估计。本文对ASV-N和ASV-T模型的参数估计,借助基于MCMC算法的OPENBUGS软件实现。
2.3 模型判断
比较传统的ASV-N模型和改进的ASV-T模型时,采用Spiegelhalter等[12]提出的DIC信息准则判别模型的适应性和复杂程度。具体形式如下:DIC=+PD,其中表示模型拟合数据的优劣程度,取值越小则模型对数据的拟合越好;PD衡量模型的复杂度,取值越大则模型越复杂。综合考虑,DIC值越小的模型对数据的拟合程度越好。
3 实证分析
3.1 数据的选取与处理
波罗的海航交所发布的BDI是干散货航运市场的综合运价指数,当前由BCI、BPI、BHSI和BSI四个分船型运价指数加权计算而成,而各分船型运价指数又由其分航线运价指数加权构成,因而具有典型代表性。本文选取2007-1-5至2015-12-31的BDI共2243个数据作为研究对象,分别应用ASV-N模型和ASV-T模型进行实证研究。首先用公式R1=logPt-logPt-1将原始干散货运价指数BDI转化为对数收益率序列,记为RBDI。

图1 BDI对数收益率序列
3.2 数据的平稳性和正态性检验
在对数据建立模型之前,首先对原始的干散货运价指数BDI和对数化收益率序列RBDI进行单位根检验。表1的ADF检验结果表明经过对数化差分的RBDI序列是平稳的过程。

表1 BDI和RBDI序列的ADF检验结果

表2 数据的描述性统计分析
样本数据的对数收益率序列RBDI的基本统计特征结果见表2,RBDI序列的峰度值大于标准正态分布的峰度值3,且J-B正态性检验的统计量大于显著水平为5%时的临界值5.99,因而拒绝RBDI序列服从正态分布的假设,干散货运价收益分布存在厚尾特征。
3.3 模型比较和参数收敛性诊断
通过OPENBUGS软件对数据进行仿真分析,参考Meyer等[13]和Omori等[14]的研究,设定待估参数的先验分布分别为μ~N(0,1),(φ+1)/2~Beta(20,1.5),1/τ2~Gamma(2.5,0.025),ρ~U(-1,1),v~Gamma(16,0.8)I(4,30)。首 先 对 每 个 参 数 进 行10000次迭代作为退火期,以保证每个待估参数的两条Markov链的收敛性,再进行100000次迭代得到模型的DIC值和待估参数的模拟值。

表3 两个模型的DIC值对比

图2 参数ρ2的动态演进图
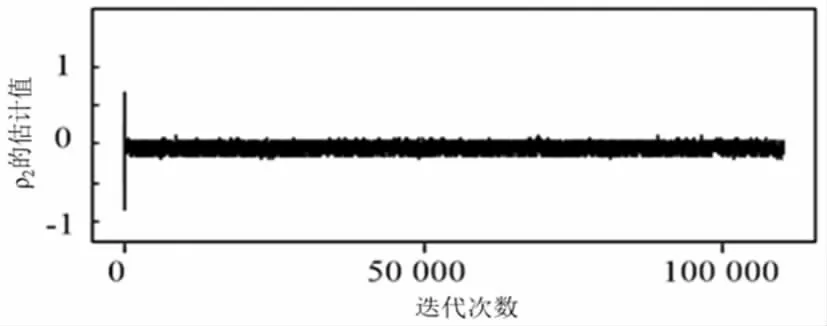
图3 参数ρ2的动态演进图
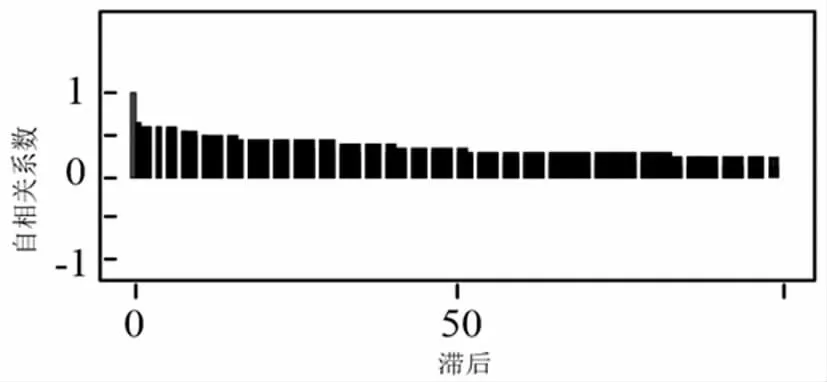
图4 参数ρ2的自相关图

图5 参数ρ2的Gelman-Rubin检验图
分析表3可知,ASV-T模型的DIC值小于ASV-N模型的DIC值,厚尾分布的ASV-T模型不仅能捕捉到干散货运价波动特征中存在的杠杆效应,而且相对于正态分布的ASV-N模型对其收益率序列分布的尾部拟合能力更强,因此我们认为改进的厚尾分布的ASV-T模型相对于传统的ASV-N模型对干散货运价收益序列的拟合程度更强,刻画的波动性特征更加全面和准确。
在MCMC方法中,待估参数的估计值通过收敛性检验才能接受其估计值。以ASV-T模型中参数ρ2为例,在图2所示的动态演进图中可观察到两条Markov链充分混合,历史路径图(图3)基本趋于稳定,在自相关图(图4)中经过打薄处理后不再有记忆性,因此可以定性判断参数ρ2的估计值是收敛的。另外根据Gelman-Rubin收敛性诊断法也从定量角度证实了这一点,由图5可知bgr值稳定的趋近于1(当1<bgr<1.2时,认为Markov链收敛)。同理,可得模型中的其他待估参数也通过收敛性检验。
3.4 参数估计结果

表4 ASV-T模型的参数估计结果
表4给出了BDI的收益率的ASV-T模型的参数估计结果。其中,表征波动持续性水平的φ后验均值高达0.9017,且落入95%的置信区间[0.8716,0.9283]之内,说明干散货运价一直处于持续的波动过程中,航运企业、租船人和其他FFA投资者在干散货航运市场的投资和决策蕴含着巨大的风险,而且这种风险有很强的持续性而这种波动的持续性是杠杆效应存在的前提。
表征杠杆效应程度的参数ρ2的后验均值为-0.04741,对应的95%的置信区间为[-0.1166,0.02274],这表明干散货运价指数收益率yt和波动程度ht+1之间存在显著的负相关关系,即受信息冲击影响的干散货运价波动存在“放大利空,缩小利好”的非对称特征(杠杆效应),在干散货航运市场这种杠杆效应的程度又小于其在股票和汇率市场。
参数v控制干散货运价收益分布尾部的“厚薄”状况,从估计结果得到的后验均值为10.09,验证了干散货运价指数的收益分布具有明显的厚尾特征,传统的正态分布假定并不符合干散货航运市场收益分布的实际特征,并且会高估杠杆效应的程度。
4 结论
近年来,干散货航运市场大起大落,干散货运价剧烈波动,在考虑了极端风险情况后,改进的厚尾分布非对称随机波动模型对干散货运价波动的杠杆效应特征刻画更加准确和优越。从长期来看,在股票和期货市场普遍存在的由信息冲击引起的杠杆效应在干散货航运市场是显著的,即在同等强度的利空消息冲击要比利好消息冲击引起干散货运价更大的波动。
羊群效应在一定程度上可以解释干散货运价波动的杠杆效应,航运市场具有信息透明的特点,在利空信息冲击下引起的市场恐慌会引起干散货运价更大的波动。近年来以FFA为代表的海运金融衍生品市场空前繁荣,航运企业、租船人和国际金融机构等通常采取“追涨杀跌”的正反馈交易策略,在一定时期内,FFA市场日益偏离其运费风险管理和价格发现的初衷,成为国际资本投机炒作的对象。在2008年经济危机前后,金融机构从FFA大举撤资,引发了FFA市场的恐慌性抛售和BDI的“断崖式”下跌。
当前,全球工业活动低迷,大宗商品和能源航运需求不振,作为国际航运重要驱动力的新兴市场国家经济增速放缓,都造成了干散货航运市场需求不足,而新船的持续交付又加剧了运力过剩,在一系列利空消息冲击不断的情况下,对干散货运价波动的杠杆效应特征的把握在行业萧条期就显得至关重要。

