排序集抽样下指数分布的产品可靠度研究

董晓芳， 张良勇

（河北经贸大学 数学与统计学学院，河北 石家庄050061）

0 引言

排序集抽样（Ranked set sampling，RSS）方法是澳大利亚农业学家McIntyre［1］在估计农场牧草产量时提出的，已被广泛应用到临床医学、系统可靠性、管理工程、生态环境等领域［2～7］。排序集样本不仅包含了样本信息，还包含了次序信息，在实际中只要感兴趣的样本不易具体测量，但较容易直观排序时，RSS方法比简单随机抽样（Simple random sampling，SRS）方法更加有效。例如，Risch和Zhang［2］在《Science》上论证了对配对亲属进行RSS，遗传相关性试验效率能得到显著地提高。

指数分布在可靠性试验中占有非常重要的地位，它可以很好地用来描述某些电子元器件的寿命［8］。产品可靠度是描述产品可靠性的重要度量指标［9］。若产品寿命T服从指数分布，t0表示规定的时间，则T的可靠度为

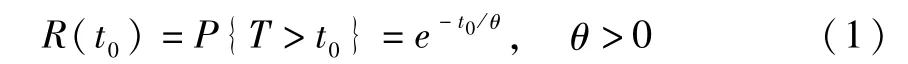
其中θ为未知参数。近年来，一些学者研究了RSS下R（t0）的估计问题。El-Neweihi和Sinha［10］首次指出RSS样本单元T（i）j可看作可靠性工程中表决系统i／m（F）的寿命时间，并利用此关系构造了RSS下R（t0）的无偏估计量。Ghitany［11］进一步证明了文献［10］的RSS无偏估计量一致优于SRS下相应估计量，但通过举例指出文献［10］中最优估计量的方差并不是最小的。Sinha等［12］利用RSS样本的次序统计量构造了R（t0）的无偏估计量，并分析了其统计性质。

文献［10～12］均通过比较RSS下估计量与SRS下相应估计量的估计效率，证明了RSS方法的高效率性。但是，这些文献都是采用RSS经验分布函数来构造可靠度的估计量。我们知道当总体分布已知时，极大似然估计是寻求点估计的最重要方法，应用很广［9］。针对指数分布可靠度的估计问题，本文研究基于RSS方法的MLE及其修正估计，分析它们的统计性质，并进行估计效率的理论比较和实际应用比较。

1 RSS下产品可靠度的MLE

本节分析RSS下R（t0）的MLE及其渐近分布。首先简要介绍RSS方法的抽样过程及其样本特点。

1.1 RSS方法

RSS方法的具体抽样过程为：

第一步，从总体中抽取样本量为m2的简单随机样本，随机划分为m组，每组m个；

第二步，利用直观感知的信息对每组样本进行由小到大的排序，这些信息包括专家观点、主观经验判断以及一些易于获得的信息，但不包括与所推断量有关的具体测量；

第三步，从第i个排序小组中抽出次序为i的样本单元，i＝1，2，…，m。

以上整个过程称为一次循环，为了增大样本量，循环重复k次。若令T（i）j表示在第j次循环中从第i组中抽出次序为i的样本单元，则排序集样本表示为：

最终只对这n＝mk个样本单元进行实际测量。排序集样本的显著特点有：（i）排序集样本单元之间相互独立；（ii）每一行的样本单元之间独立同分布；（iii）每一列都包含了各个秩次的信息。

1.2 R（t0）的MLE

令产品寿命T的分布函数和概率密度函数分别为F（t）＝1-e-t／θ和f（t）＝e-t／θ／θ。令T（i）j，i＝1，2，…，m；j＝1，2，…，k为抽自的排序集样本，则T（i）j的概率密度函数为

显然，T（i）j的分布与j无关。

由式（2），RSS下θ的似然函数为

（3），RSS下θ的对数似然函数为

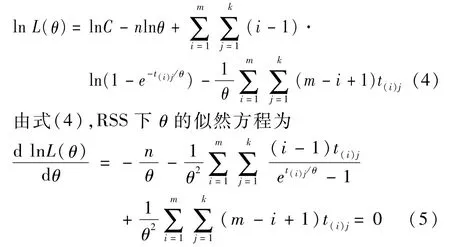
下面定理证明了（t0）的存在性和唯一性。

定理1对于任意给定的小组数m、循环次数k和规定时间t0，（t0）存在且唯一。

证明根据式（5），得

令IRSS（θ）表示RSS下θ的Fisher信息。由Chen等［13］可知，指数分布的次序统计量满足Fisher信息的常规条件，于是IRSS（θ）存在。再根据T（i）j，j＝1，2，…，k的独立同分布性和式（5），得

式（9）中＝t（i）1／θ表示标准指数分布的RSS样本单元。

定理2对于给定的小组数m和规定时间t0，当n→∞（k→∞）时，有

证 明渐 近 正 态 性 的 证 明 可 以 通 过dlnL（θ）／dθ的泰勒级数展开式和中心极限定理来实现，采用的方法与SRS方法相似，这里就不再详述。再根据式（9）和（10）的渐近方差为

定理得证。

根据文献［13］中定理3.8的推论，我们可以得到下面引理。

引理1若φ＝φ（θ）是θ的一个可导函数，且关于θ具有渐近正态性。则φ（）关于φ（θ）具有渐近正态性，且其渐近方差为（θ）［dφ（θ）／dθ］2。

下面定理证明了（t0）的渐近正态性。

定理3对于给定的小组数m和规定时间t0，当n→∞（k→∞）时，有

再将式（15）及式（12）的第二个等式代入式（16）即可得式（14）。定理得证。

2 RSS下产品可靠度的修正MLE

显然，式（17）很难求出显式解。为了解决这一问题，下面我们采用Mehrotra和Nanda［14］的部分期望法对MLE进行修正。

3 相对效率

令Ti，i＝1，2，…，n为抽自T的简单随机样本。由茆诗松等［15］知，SRS下θ的MLE为，其中n。这样，SRS下R（t0）的MLE为

3.1 渐近相对效率

下面定理证明了0）的渐近正态性，并给出其渐近方差。

定理4对于给定的小组数m和规定时间t0，当n→∞时，有

证明由文献［15］可知，SRS下θ的Fisher信息ISRS（θ）＝n／θ2，并且当n→∞时，有（-θ）N（0，θ2）。再由文献［13］知，引理1对于SRS方法依然成立。于是（t0）具有渐近正态性，且（t0）的渐近方差为

定理得证。

上式中最后等式是由式（14）和（23）所得。由式（11）知，ARE（（t0），（t0））仅与小组数m有关。

表1给出了当m＝2，3，4，…，10时ARE（（t0），（t0））的取值。可以看出m，对于任意给定的，ARE（（t0），（t0））＞1，这 说 明（t0）的估计效率一致高于（t0），并且随着m的增大（t0）的相对优势越明显。

表1 （t0）与（t0）的渐近相对效率

表1 （t0）与（t0）的渐近相对效率

m 2 3 4 5 6 7 8 9 10 ARE 1.4041 1.8082 2.2123 2.6165 3.0206 3.4247 3.8288 4.2329 4.6370

3.2 模拟相对效率

为了比较（t0）与（t0）的估计效率，我们进行了计算机模拟，模拟次数为10000次。一个估计量的偏差和均方误差分别定义为

（t0）与（t0）的模拟相对效率（Simulation relative efficiency，SRE）定义为它们均方误差比的倒数，即

表2给出了当k＝10、m＝3，5，8、θ＝0.5，1，2和t0＝0.5θ，θ，2θ时（t0）与（t0）的偏差和相对效率。可以看出，对于任意给定的m、θ和t0，｜B（（t0））｜均小于｜B（（t0））｜，并且SRE（（t0）（t0））＞1，这些说明（t0）一致优于（t0）。另外，对于任意给定的θ和t0，SRE（（t0），（t0））随着m的增加而增大。实际上，我们对于m＝2，3，4，…，10、θ＝0.5，1，1.5，…，3和t0＝0.5θ，0.6θ，0.7θ，…，2θ都进行了模拟，结果均与表2一致。

表2 （t0）与（t0）的模拟偏差和模拟相对效率

表2 （t0）与（t0）的模拟偏差和模拟相对效率

m θ t0 B（R＾MMLE，SRS（t0）） B（R＾MMLE，RSS（t0）） SRE（R＾MMLE，RSS（t0）），R＾MLE，SRS（t0））3 0.5 0.5θ -0.00790 -0.00457 1.85320 θ-0.00676 -0.00334 1.79489 2θ -0.00026 -0.00011 1.73452 1 0.5θ -0.00722 -0.00403 1.73919 θ-0.00654 -0.00278 1.76729 2θ -0.00027 0.00023 1.68713 2 0.5θ -0.00787 -0.00447 1.85541 θ-0.00611 -0.00305 1.77283 2θ 0.00043 -0.00001 1.73716 5 0.5 0.5θ -0.00512 -0.00164 2.68006 θ-0.00442 -0.00167 2.48937 2θ -0.00008 0.00003 2.56475 1 0.5θ -0.00409 -0.00144 2.56489 θ-0.00344 -0.00141 2.46309 2θ -0.00010 0.00003 2.47106 2 0.5θ -0.00425 -0.00227 2.62846 θ-0.00371 -0.00161 2.48012 2θ 0.00007 -0.00005 2.44036 8 0.5 0.5θ -0.00281 -0.00079 3.74360 θ-0.00189 -0.00055 3.71482 2θ -0.00039 0.00033 3.47553 1 0.5θ -0.00341 -0.00091 3.77391 θ-0.00253 -0.00092 3.73931 2θ -0.00009 0.00000 3.63831 2 0.5θ -0.00351 -0.00043 3.84700 θ-0.00189 -0.00080 3.77170 2θ -0.00002 0.00000 3.55154

4 应用

本节将排序集抽样方法应用到临床医学研究中，我们采用Royston等［16］给出的医学研究委员会RE01转移性肾癌试验数据。RE01试验给出了323名肾癌病人的缓解时间（月），并已证实缓解时间服从参数θ＝22的指数分布。为了比较（t0）与（t0），我们把所有病人的缓解时间作为总体。由于总体单元数不多，我们取排序小组数m＝3，4，5，循环次数k＝5，RSS方法和SRS方法都采用放回式抽样，抽样次数为20次。表3和表4分别给出了样本量n＝15（m＝3）的一次排序集样本值和一次简单随机样本值。

表3 排序集抽样下转移性肾癌病人的缓解时间（月）

表4 简单随机抽样下转移性肾癌病人的缓解时间（月）

表5给出了当m＝3，4，5（n＝15，20，25）和t0＝11，22，44时（t0）与（t0）的偏差和均方误差。可以看出对于给定的m和t0，｜B（（t0））｜小于｜B（（t0））｜，且MSE（（t0））小于MSE（（t0））。另外对于给 定 的t0，MSE（（t0））／MSE（（t0））随着m（n）的增加而增大，即RSS相对于SRS的优势越明显。应用结果进一步验证了（t0）优于（t0）。

表5 转移性肾癌数据中S（t0）与（t0）的偏差和均方误差

表5 转移性肾癌数据中S（t0）与（t0）的偏差和均方误差

m n t0 B（R＾MLE，SRS（t0）） B（R＾MMLE，RSS（t0）） MSE（R＾MLE，SRS（t0）） MSE（R＾MMLE，RSS（t0））3 15 11 -0.02030 -0.01498 0.00723 0.00540 22 -0.01631 -0.01203 0.00871 0.00608 44 0.00185 -0.00084 0.00448 0.00202 4 20 11 -0.01264 -0.01105 0.00510 0.00222 22 -0.00768 0.00734 0.00664 0.00399 44 0.00145 -0.00049 0.00333 0.00109 5 25 11 -0.01645 -0.00959 0.00398 0.00169 22 -0.00775 -0.00280 0.00531 0.00227 44 0.00092 -0.00071 0.00273 0.00089

5 结论

针对指数分布产品可靠度的估计问题，本文研究了RSS下可靠度的MLE及其渐近分布，并给出带有具体表达式的修正MLE。渐近相对效率和模拟相对效率的研究结果均表明：RSS下MLE和修正MLE的估计效率都一致高于SRS下MLE。临床医学的实际应用结果进一步验证了理论研究结果的正确性。另外，在实际应用RSS方法时，为了减少排序误差，我们可以参考文献［17］进行排序。