基于φ-OTDR光纤振动传感系统模式识别方法

王兴奇, 朱 瑞, 李欣城, 黄丹飞, 荆 涛, 衣文索

(1. 长春理工大学 光电工程学院, 长春 130022； 2. 吉林大学 汽车工程学院, 长春 130022)

分布式光纤振动传感系统利用光纤作为传感媒介, 基于光的干涉或后向散射原理进行高灵敏度振动监测. 光纤具有功耗低、 抗电磁干扰强、 灵敏度高、 成本低、 布设灵活及场景应用广泛等特点[1-3], 在管涌监测、 桥梁健康监测及周界安保监测等领域应用广泛. 其中相位敏感光时域反射计(φ-OTDR)的分布式光纤振动传感系统传感机构简单(一根传感光纤), 可对同一时刻不同位置的多个振动点进行同时识别定位, 且分辨率及定位精度高.

Taylor等[4]首次提出的φ-OTDR系统, 与传统光时域反射计(OTDR)相比, 其注入光为强相干光, 输出光为后向Rayleigh散射光的相干干涉光. 目前对提高φ-OTDR系统分辨率及传感长度的研究较多, 而对振动信号模式识别的研究较少. Tan等[5]以信号强度为识别依据在埋地环境下对人工挖掘、 车辆经过及挖掘机挖掘3种模式进行了振动信号的识别研究； 张颜等[6]以信号平方差、 短时过电平率及短时Fourier变换等特征参量为识别依据, 对敲击、 攀爬和浇水等模式进行识别, 在时域和频域上进行分析, 但识别正确率较低, 且对相似度较高的扰动识别困难； 彭宽等[7]以平均片段间隔、 片段长度和峰均比、 频域能量等特征参量, 对脚踩、 自行车轧过和拍击等模式进行识别, 识别正确率较高, 但对相似模式识别能力较差.

利用φ-OTDR的分布式光纤振动传感系统信号特点, 本文提出一种基于多种综合特征提取的模式识别方法. 该方法提取信号主波能量(MVE)、 信号主瓣时延(MVBW)、 信号主波峰峰值(MDV)、 信号主波Q值(MVQV)、 信号频谱(SFS)、 3 dB时延(3 dB BW)、 主瓣峰值(MVMAX)、 中心频率(CF)、 二次回波损耗(2VEL)、 波数(SSWC)、 半波长度(HWDT) 11种特征参量作为参考衡量标准, 用模糊评价矩阵算法进行模式识别, 从而提高了识别准确性, 且对相似度较高的扰动目标有较强的识别能力.

1 φ-OTDR实验系统及原理

φ-OTDR与传统OTDR系统的结构近似, 由于φ-OTDR系统采用窄线宽激光器作为光源, 因此其传感光纤内光脉冲信号有较强的相干性.φ-OTDR系统检测的是光脉冲信号相位变化导致的光强变化量, 其原理如图1所示. 脉冲光传输如图2所示. 由图2可见: 窄线宽激光器发出超窄线宽激光, 经声光调制器后, 连续激光被调制为一定频率和一定脉宽的脉冲光； 脉冲激光经掺铒光纤放大器放大入射功率, 经环形器进入传感光纤; 脉冲激光在传感光纤内产生Rayleigh散射现象, 由Rayleigh散射现象产生的后向Rayleigh散射光会沿环形器进入雪崩光电二极管(APD)光电探测器, 将光信号转变为电信号, 采集电信号并用电脑进行分析.

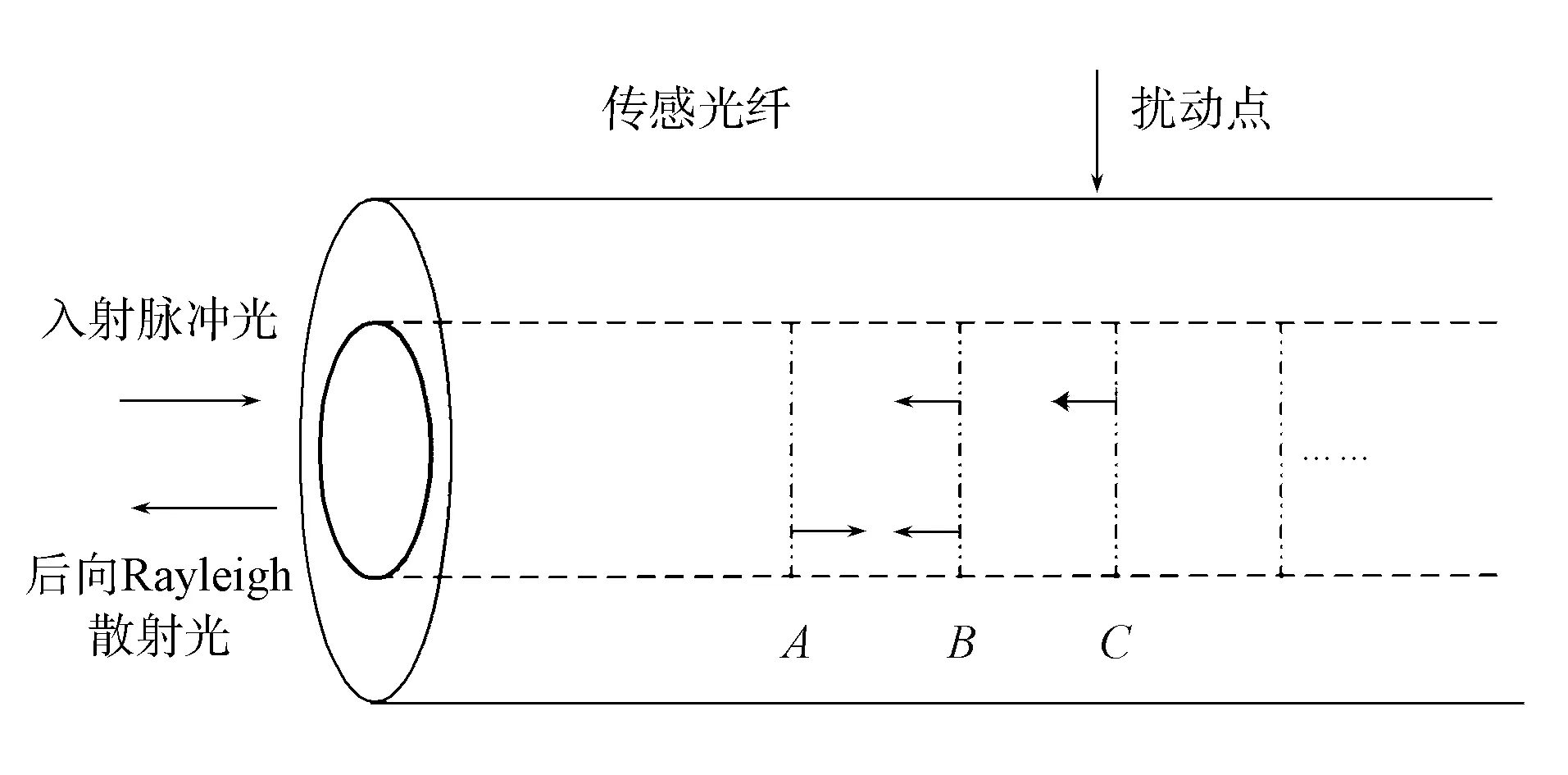
图1 系统原理Fig.1 System principle

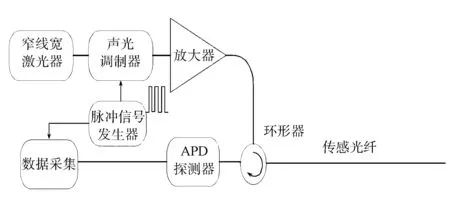
图2 脉冲光传输Fig.2 Pulse light transmission

A点的脉冲光信号表达式为

EA(t)=ER0(t)exp{i[2πfct+φ0(t)]},

(1)

其中:ER0(t)为A点光强;fc为光频率；φ0(t)为无扰动时光相位. 当C点有扰动信号时, 光信号会受扰动信号的作用, 其相位发生改变,C点的后向Rayleigh散射信号可表示为

EC(t)=ER1(t)exp{i[2πfct+φ1(t)]},

(2)

其中:ER1(t)为C点的后向Rayleigh散射光光强;φ1(t)为光纤扰动信号影响后的光相位.

A点光信号传输到B点产生后向Rayleigh散射光, 其强度为ER0, 该信号与C点的后向Rayleigh散射光产生叠加, 传输到探测器时产生干涉， 可表示为

EB(t)=ER0(t)exp{i[2πfct+φ0(t)]}+ER1(t)exp{i[2πfct+φ1(t)]}.

(3)

此时, 在探测器中的信号可表示为

(4)

由于扰动信号影响, 因此同一位置在不同时间的后向Rayleigh散射光强会有较大改变, 为提高信噪比, 将不同时间点的后向Rayleigh散射光信号进行差分, 并对差分信号进行分析. 提取空域特征参量, 对同一位置不同时间点采集时域特征参量.

2 复合特征参量模式识别

由于扰动目标特征的多样性和易变性, 用单一特征向量难以准确鉴别出目标类别, 因此需充分、 有效地利用多种特征信息, 进行各特征融合. 特征融合的有效性主要取决于特征参量的特殊性及多角度性. 用多角度多特征提取信号的不同特征参量, 可有效突出不同模式的扰动特性.

本文主要选取的特征参量包括MVE,MVBW,MDV,MVQV,SFS. MVE如图3所示. 按采样平率离散得到信号幅度平方的积分, 能量即为主波信号内各点幅度值V平方后求和,

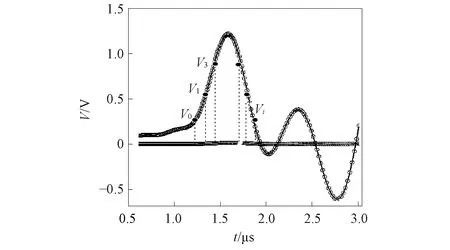
图3 主波能量Fig.3 Main wave Energy

即振动信号主波能量反映目标信号的强度信息, 计算结果可衡量目标的能量大小. 由图3可见, 在Rayleigh分布式光纤信号回波信号中, 振动能量大的MVE大, 振动能量小的MVE小.

MVBW如图4所示. MVBW描述扰动信号主瓣每次扰动的时延, 体现了扰动信号的时域特性, 通过对MVBW进行计算可有效提取振动信号的时域信息， 计算公式为

(6)

MDV如图5所示. MDV描述信号在单周期内回波信号的主波峰峰值, 利用离散采样得到的信号, 主波峰峰值可衡量信号瞬时强度信息, 为正向最高峰电压与反向最低电压差, 计算公式为

MDV=MVMAX-MVMIN.

图4 主瓣时延Fig.4 Main lobe delay

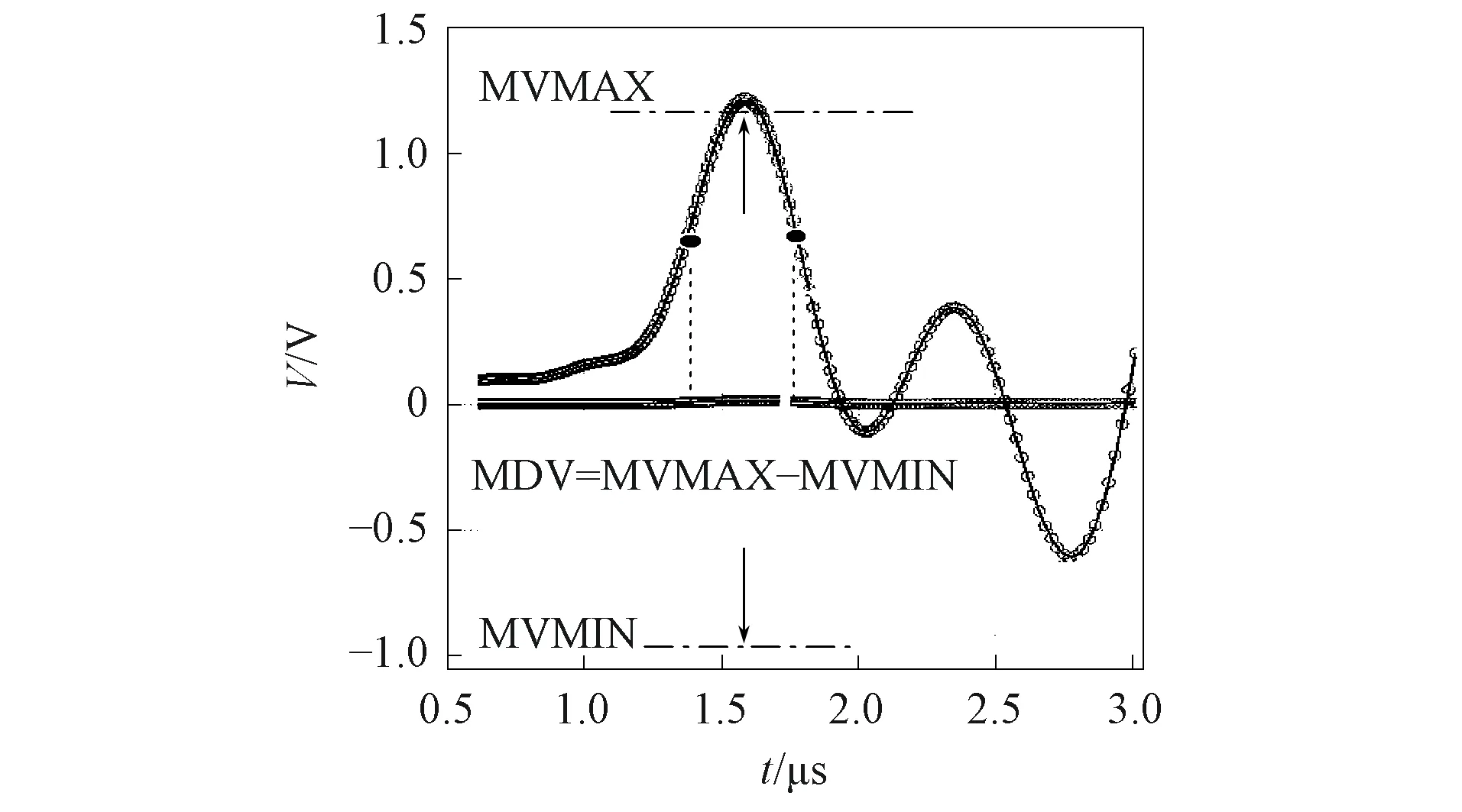
图5 主波峰峰值Fig.5 Main peak value

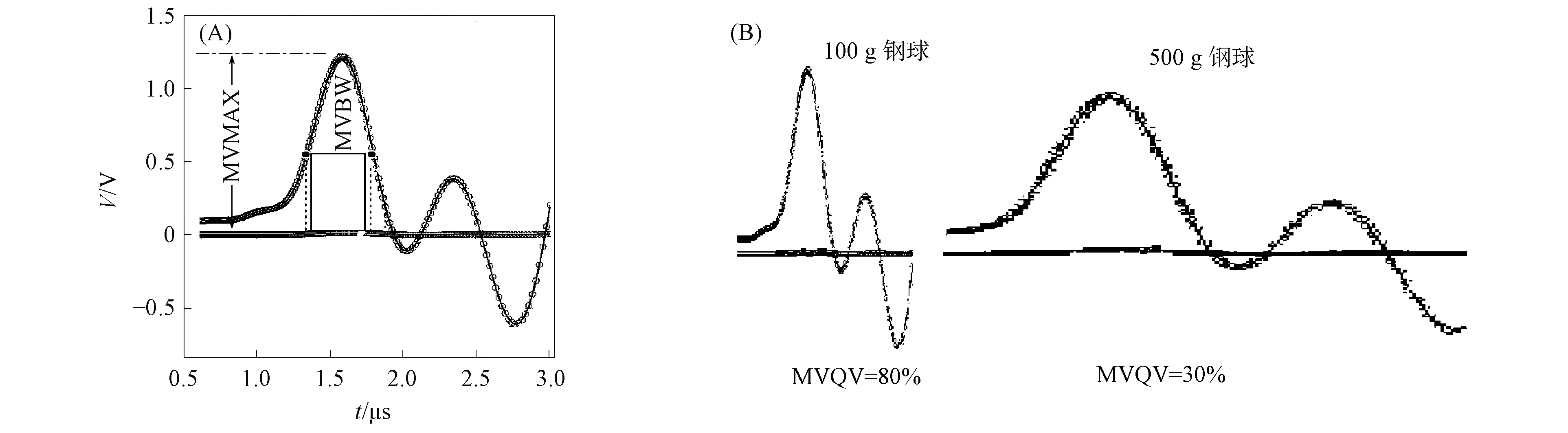
图6 主波Q值Fig.6 Main wave Q value

MVQV如图6所示. MVQV描述来波信号主能量的尖锐程度. 由图6(B)可见: 瞬时敲击和挖掘破坏等信号的MVQV较尖锐, 即能量集中、 较窄且尖锐程度大的MVQV大； 车辆经过或下雨等的MVQV较平坦, 即能量分布宽且尖锐程度小的MVQV小. 其计算公式为MVMAX与MVBW的比值, 即

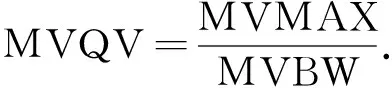
(7)

SFS描述扰动信号的振动频率. 通过测定信号穿过电平阈值的次数得到信号频率, 其表示在时间阈值内信号在电平阈值附近穿越的频率, 计算公式为

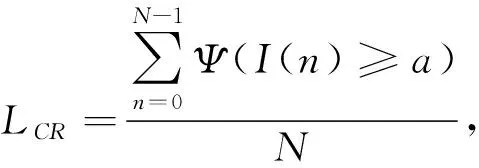
(8)

其中：I(n)为信号点幅度；a为设置的电平阈值；Ψ为指示函数. 当I(n)≥a时,Ψ=1; 否则Ψ=0. 由于短时过电平率与传感信号的短时平均频率以及短时相位变化呈正相关, 因此, 可用SFS作为信号的特征.

此外, 3 dB BW表示信号能量衰减到原始功率1/2状态的时间； MVMAX表示信号主瓣幅值； CF表示信号的频率参数； 2VEL表示振动信号的主波振荡后的二次回调峰值； SSWC表示信号波形变化率； HWDT表示在一个周期内一个峰值升起到结束的时间.

3 多特征参数的模糊评价矩阵

本文通过提取φ-OTDR光纤分布式传感系统信号中的特征参数构成一个模糊因素集X={AMVE,BMVBW,CMDV,DMVQV,ESFS,…,K2VEL}. 根据模糊数据的理论基础[8], 构建模糊因素变量X对应的模糊辩识对象集A的模糊隶属函数与模糊评判矩阵.

为讨论问题的一般化, 设有n类模式识别对象A1,A2,…,An, 每类的特征集X有m个特征参数. 因此, 模糊因素变量X={x1,x2,…,xm}对应模糊识别对象集A={A1,A2,…,An}的模糊隶属函数分别为{μA1(x),μA2(x),…,μAn(x)}. 假设特征参量是正态分布模糊集, 测量值的第j个指标对识别对象Ai的隶属函数为

(9)

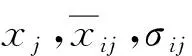
(10)

其中rij=μA1(xj)为测量值X的第j个指标对辨识对象Ai的隶属函数.

根据模糊评判矩阵R, 用模糊推理的相应标准和方法进行推理判决, 可推断得到测量值X归属于某一识别对象.

4 结果与讨论

用线宽为10 kHz超窄线宽激光器作为光源发出1 550 nm激光, 先经声光调制器(AOM)产生频率为2 kHz, 脉冲宽度100 ns的脉冲激光后, 再经掺铒激光放大器(EDFA)放大激光入射功率至54.6 μW后进入长度为22.6 km单模裸光纤, 后向Rayleigh散射光由探测器接收滤波放大后进入采集卡(采集卡采集频率为2 MHz), 结果如图7所示. 采集多次信号数据后, 通过滑动平均算法得到差动数据, 结果如图8所示. 在上位机中用LABVIEW软件进行信号阈值判断及报警预测, 对所得报警信号波形进行分析判断及模式识别, 得到最终结果.

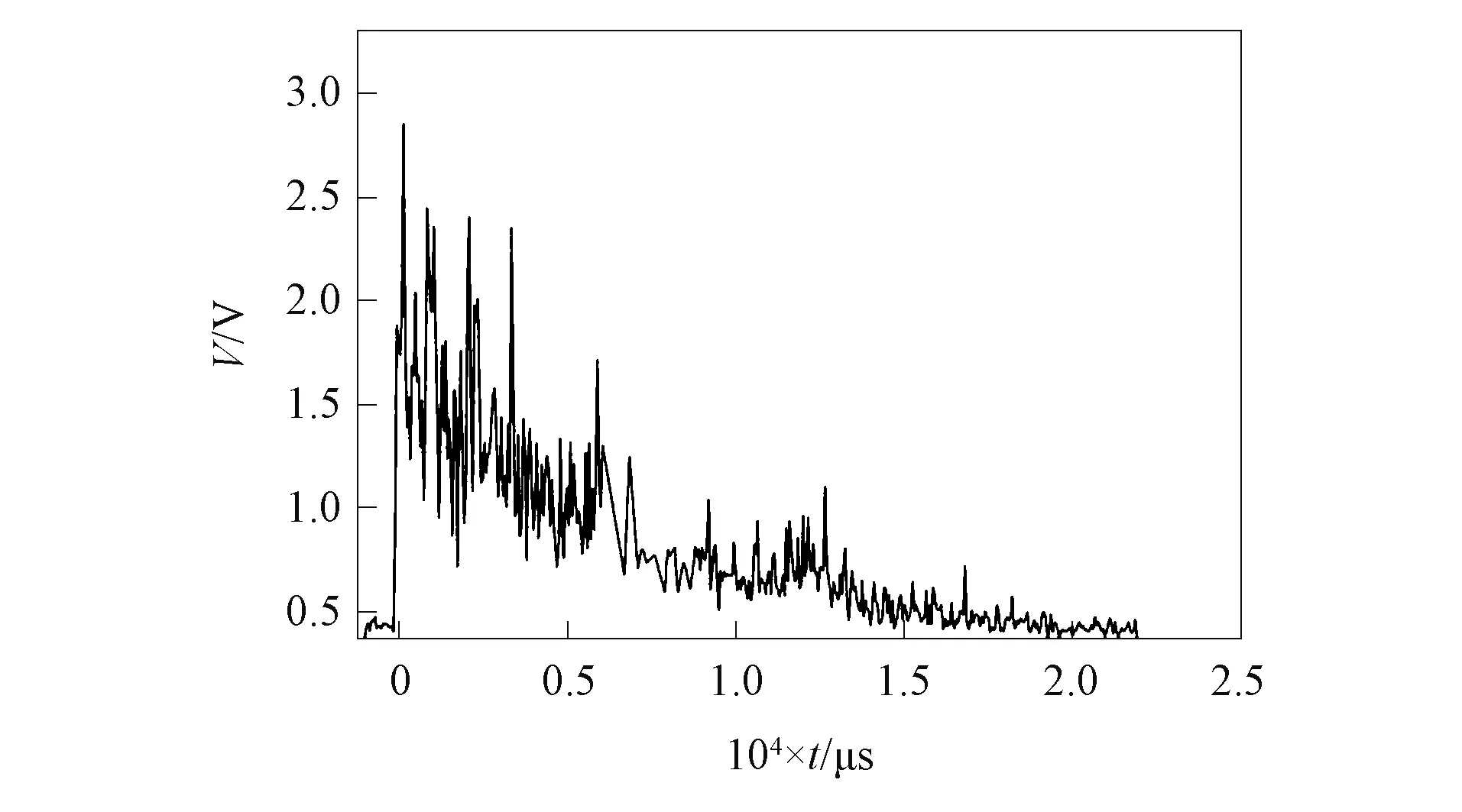
图7 Rayleigh信号Fig.7 Rayleigh signal

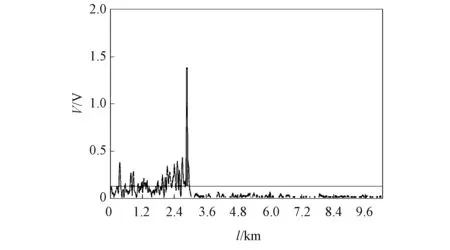
图8 差动数据Fig.8 Differential data

实验将500,100 g钢制实心球分别在距单模裸光纤10,50 cm处, 高度为100 cm处释放. 为得到更稳点数据样本, 实验分为4组： (500 g,10 cm)， (500 g,50 cm)， (100 g,10 cm)， (100 g,50 cm), 每组实验进行50次, 得到200个样本. 每组10次取一次平均值, 共得到20组数据, 结果列于表1. 由表1可见: (500 g,10 cm)组的振动能量大, 幅值高, 信号波形较宽, 2次回波损耗较低； (500 g,50 cm)组低于(500 g,10 cm)组的能量, 但明显高于100 g组的能量； (100 g,10 cm)组振动能量较小, 信号波形尖锐且二次回波损耗较高； (100 g,50 cm)组的振动能量最低, 信号波形小而尖锐.

表1 20组平均数据

根据多特征参量模式识别理论, 将待识别数据分为11种特征参量, 利用表1中的目标库数据, 通过式(9)分别得到待识别振动信号的11种候选扰动模式的隶属函数. 每个待识别扰动信号有11个隶属函数值, 这11个隶属函数值构成了待识别信号的多目标模糊评价矩阵, 通过式(10)得到最大评价函数值对应的候选扰动模式, 即为模式识别结果.

信号的MVE,SFS,MVBW及2VEL可大致体现信号主体特征. 针对相同目标库, 对仅提取这4种特征参量与提取11种多特征参量的扰动模式识别方法进行对比, 识别结果列于表2.

表2 识别结果

由表2可见, 利用多特征参量进行模式识别方法的识别率分别为96.25%,91.25%,92.50%,83.75%, 综合识别率90.87%, 明显高于4种特征参量的识别方法. 因此， 多特征参量的模式识别方法可解析出扰动信号中更多的识别信息, 更有利于识别相似度较高的扰动模式.

综上, 本文通过提取信号主波能量(MVE)、 信号主瓣时延(MVBW)、 信号主波峰峰值(MDV)、 信号主波Q值(MVQV)、 信号频谱(SFS)、 3 dB时延(3 dB BW)、 主瓣峰值(MVMAX)、 中心频率(CF)、 二次回波损耗(2VEL)、 波数(SSWC)和半波长度(HWDT)等11种特征参量, 用模糊评价矩阵算法进行识别. 结果表明, 该方法对扰动具有较高的识别率. 在工程实践中, 针对具体需求而判别特定的扰动模式, 可在11种特征参量中选取7～8种能体现明显特征的参量进行识别判定.