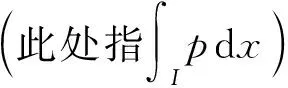求解渗流方程的一种修正的中心型有限体积法
陈国芳, 吴 丹, 吕俊良
(1. 吉林省教育学院 民族教育学院, 长春 130022; 2. 吉林大学 数学学院, 长春 130012)
0 引 言
考虑渗流方程:
其中:T<∞;m>1. 显然, 方程(1)是一个非线性退化的抛物方程. 渗流方程常用于模拟物理上的多孔介质或热扩散等问题. 文献[1]给出了标准有限元法求解该类问题的理论分析; 文献[2]采用积分方程方法研究了退化的非线性抛物问题; 文献[3]用移动网格方法研究了二维多孔介质扩散问题; 文献[4]给出了求解问题(1)的局部间断Galerkin法(LDG); 文献[5]提出了一种交错的拟态差分法(MFDM)求解该类退化问题; 文献[6-7]分别给出了改进的混合有限元法和混合有限体积元法求解退化非线性抛物问题. 由于节点型方法求解渗流方程时会出现非物理振荡, 因此文献[8]给出了3种后验修补技术; 文献[9]建立了保正且守恒的二次元有限体积法. 文献[5]研究表明, 当使用有限体积法求解退化抛物问题时, 会产生数值曲线不能有效向前传播的所谓“数值热障”现象. 这主要是因为当扩散系数等于零或趋于零时, 扩散系数在单元格上的调和平均也将等于零或趋于零, 因此数值求解时, 扩散过程不发生或几乎不发生, 导致数值界面不会随着时间的推移而向前传播. 基于此, 本文考虑改进扩散系数的数值逼近方法, 取内部边两侧单元中心点处未知量的代数平均值作为非线性扩散系数中未知量的近似. 从而避免因一侧未知量等于零或趋于零导致的“数值热障”问题.
1 标准有限体积法
首先离散时间变量, 将时间[t0,T]做如下N等分:
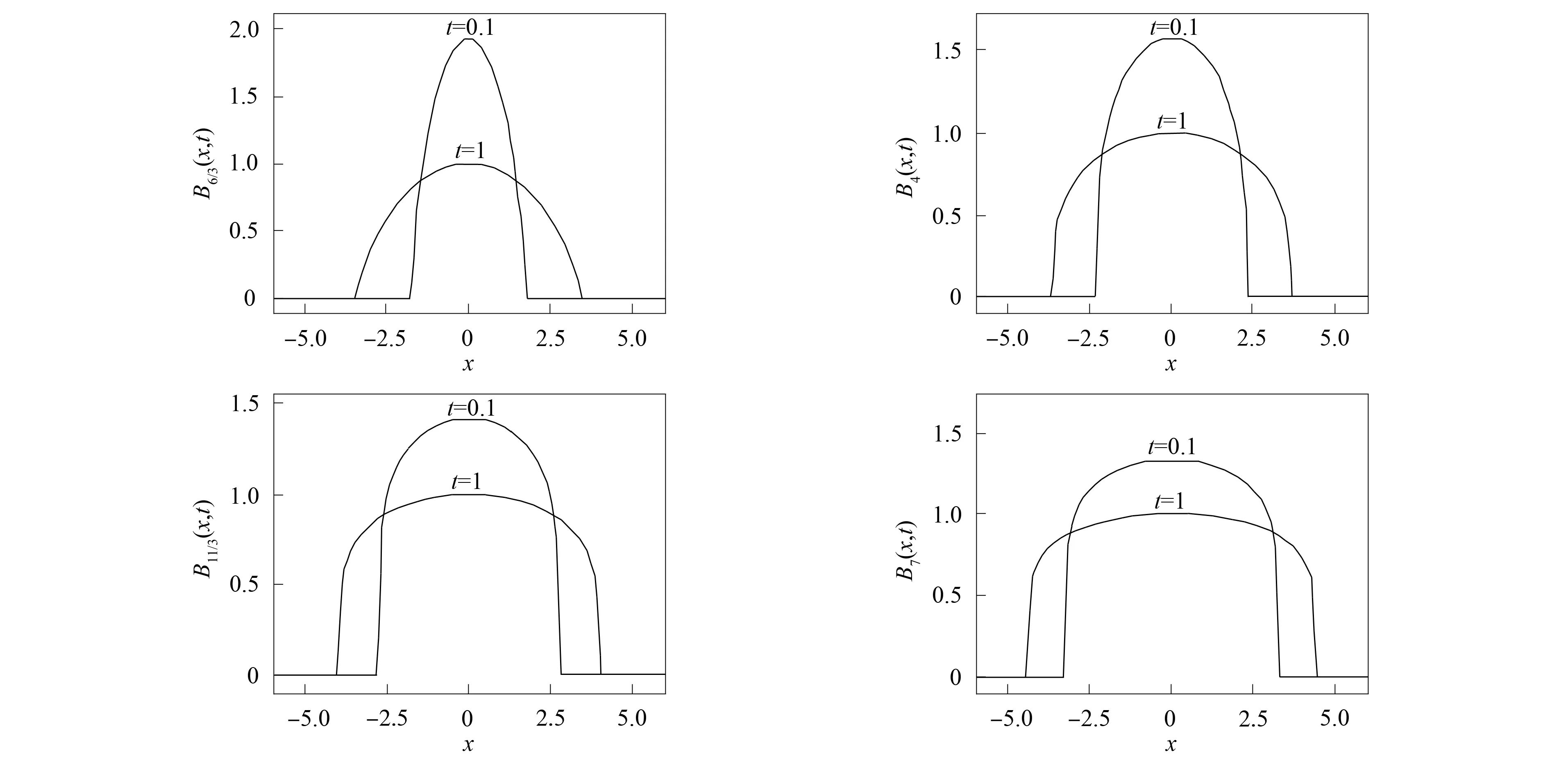
t0 其中tn=t0+n(T-t0)/N. 记K(u)=mum-1, 使用向后Euler法离散时间导数项, 得半离散方程 (4) 其中: 时间步长Δt=(T-t0)/N;u(n)是u(x,t)在时刻tn的近似. 方程(4)可进一步改写成 (5) a=x0 记任意单元Ii=[xi-1,xi]的步长为hi(i=1,2,…,M), 剖分步长h=max{hi;i=1,2,…,M}. 考虑方程(5), 在单元Ii+1=[xi,xi+1]上对方程(5)积分, 得 (6) 利用分部积分公式, 并对u(n+1)和u(n)采用中点近似, 有 (7) (8) (9) 将u(n+1)(xi+1)的表达式代入式(8), 可得流的近似为 显然当hi=hi+1时, 这里将导出扩散系数的调和平均作为非线性扩散系数的近似. 类似地, 还有 于是, 对于1≤i≤M-2, 格式为 即 (10) 类似地, 对于i=1, 格式为 (11) 对于i=M-1, 格式为 (12) (A(n+1)+B)U(n+1)=F(n+1),n=0,1,…,N-1, 其中: 实际计算中, 需使用非线性迭代法, 如Picard迭代法. 因此线性方程组可写成 (A(n+1,s)+B)U(n+1,s+1)=F(n+1),s=0,1,2,…, 其中: 这里 问题(1)的精确解称为Barenblatt解[10]: 其中u+=max{0,u}. 因此初值条件可取为g(x)=Bm(x,t0). 图1为Barenblatt解的图像. 使用1.1中推导的中心型有限体积法求解该问题的数值结果如图2所示. 由图2可见, 计算终止时刻数值波阵面未离开初始位置, 产生了数值振荡. 因此, 标准单元中心型有限体积法不适合直接求解退化抛物问题. 图1 当t=0.1,1时问题(1)的Barenblatt解Fig.1 Barenblatt solutions of problem (1) when t=0.1,1 图2 中心型有限体积法的数值结果Fig.2 Numerical results of cell-centered finite volume methods 未知函数仍定义在单元中心, 但扩散系数的近似选取单元节点处的值. 对于非线性问题, 需要用单元中心点的值组合得到单元节点的值. 考虑方程(7), 在xi+1点的流可用如下两种方式近似: (13) (14) 将u(n+1)(xi+1)的表达式代入式(13)可得流的近似: 显然这里导出扩散系数的近似不是调和平均值. 类似地, 还有 于是, 对于1≤i≤M-2, 格式为 即 (15) 类似地, 可得当i=0时的格式为 (16) 当i=M-1时的格式为 (17) 从而可得如下线性方程组: (A(n+1)+IM×M)U(n+1)=F(n+1),n=0,1,…,N-1, 其中: 这里 实际计算中, 使用非线性迭代法所得的线性方程组可写成 (A(n+1,s)+IM×M)U(n+1,s+1)=F(n+1),s=0,1,2,…, 其中: 这里 定理1格式(15)~(17)是保正的, 即若g(x)≥0, 则对每个n∈+和s∈+, 均有U(n+1,s+1)≥0. 考虑Barenblatt解问题, 使用上述推导的修正的中心型有限体积法求解, 数值结果如图3所示. 由图3可见, 新方法不仅没有“数值热障”现象, 还可以很好地捕捉波阵面且数值解保正. 图3 修正的中心型有限体积法数值结果Fig.3 Numerical results of modified cell-centered finite volume methods 表1 几种数值方法的L∞误差比较 表2 几种数值方法的L2误差比较 表3 几种数值方法保持能量守恒能力的比较 综上, 针对使用标准有限体积法求解退化问题时, 会出现数值曲线不能向前传播的所谓“数值热障”现象, 本文提出了一种修正的有限体积法, 可有效解决该问题. 新方法中非线性扩散系数的取值为相邻单元中心点处的代数平均, 从而避免了因扩散系数的调和平均近似带来的缺陷.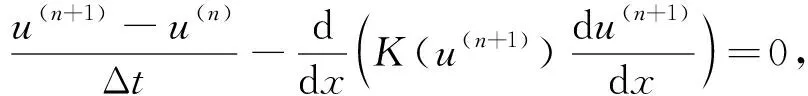


1.1 中心型有限体积法

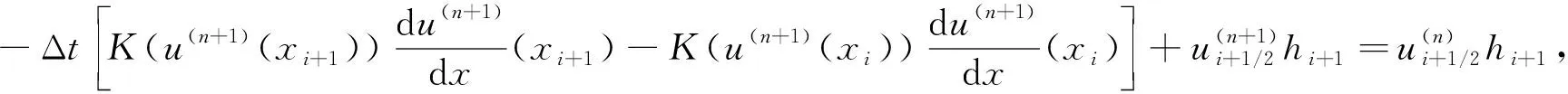







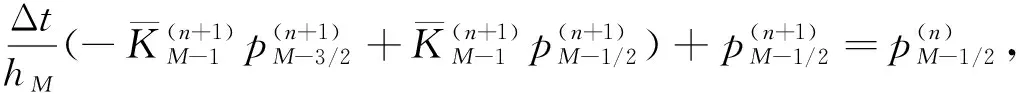

1.2 数值实例

2 修正的单元中心有限体积法
2.1 修正的中心型有限体积格式

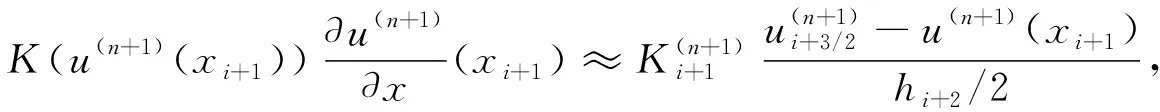

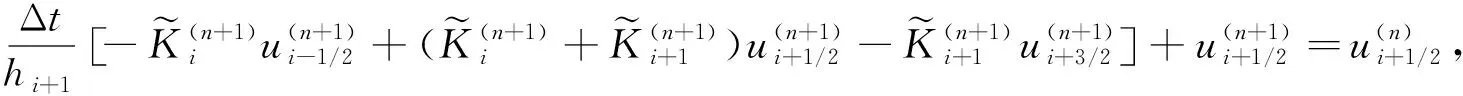
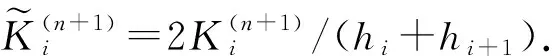



2.2 修正的中心型有限体积法数值实例