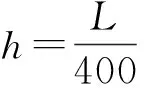美式多资产期权定价问题的有限差分法
张 琪, 左 平, 郝永乐, 杨程博, 李婷婷
(1. 沈阳工业大学 理学院, 沈阳 110870; 2. 吉林大学 符号计算与知识工程教育部重点实验室, 长春 130012;3. 空军航空大学 基础部, 长春 130022; 4. 周口师范学院 数学与统计学院, 河南 周口 466001;5. 吉林大学 数学学院, 长春 130012)
0 引 言
美式多资产期权是一种特殊的期权, 其标的物是多个原生资产的投资组合, 收益由合约中原生资产价格的加权平均值确定, 具有不同于单资产期权的套期保值效果. 由于美式多资产期权不存在显式解, 因此对其进行数值算法的研究备受关注[1-3]. 本文以二维美式看跌期权为例, 给出一种求解该问题的有效算法. 设Si,σi,qi(i=1,2)分别表示第i个风险资产的价格、 波动率和红利率, 则美式多资产看跌期权V(S1,S2,t)满足下列线性互补模型[4]:

(1)
其中:
φ(S1,S2)=max{K-α1S1-α2S2,0}.
这里K,t,r,ρ,T分别表示敲定价格、 时间、 标的资产的无风险利率、 标的资产间的相关系数和期权到期日,αi≥0(i=1,2)表示第i种原生资产所占的比例, 满足α1+α2=1.
通过变量替换
方程(1)可化为下列常系数线性互补问题:

(2)
相应的初始条件和收益函数分别为
P(x,y,0)=g(x,y), (x,y)∈2,
g(x,y)=max{K-α1ex-α2ey,0}.
其中
观察简化模型(2)易见, 在数值求解该模型时, 会面临以下难点:
1) 该模型为线性互补问题, 具有高度非线性, 很难直接求解;
2) 模型的求解区域为无界区域, 直接设计数值格式几乎不可能.
基于上述求解难点, 本文分别给出相应的处理技巧.
1 有界规则区域的定价模型
本文利用惩罚法和完全匹配层(PML)技巧将定价模型转化为有界区域上的非线性抛物问题. 利用惩罚法求解期权定价问题[5]主要通过加惩罚项将线性互补问题转化为抛物问题, 形式如下:

(3)
引理1[6-7]如果Pη和P分别为模型(3)和模型(2)的解, 则下列估计式成立:
处理无穷区域问题的有效方法----PML技巧[8], 其主要思想是在求解区域的截断处添加一个非反射的吸收层, 以减弱数值反射的影响, 进而达到减少误差的目的. 令有界区域为
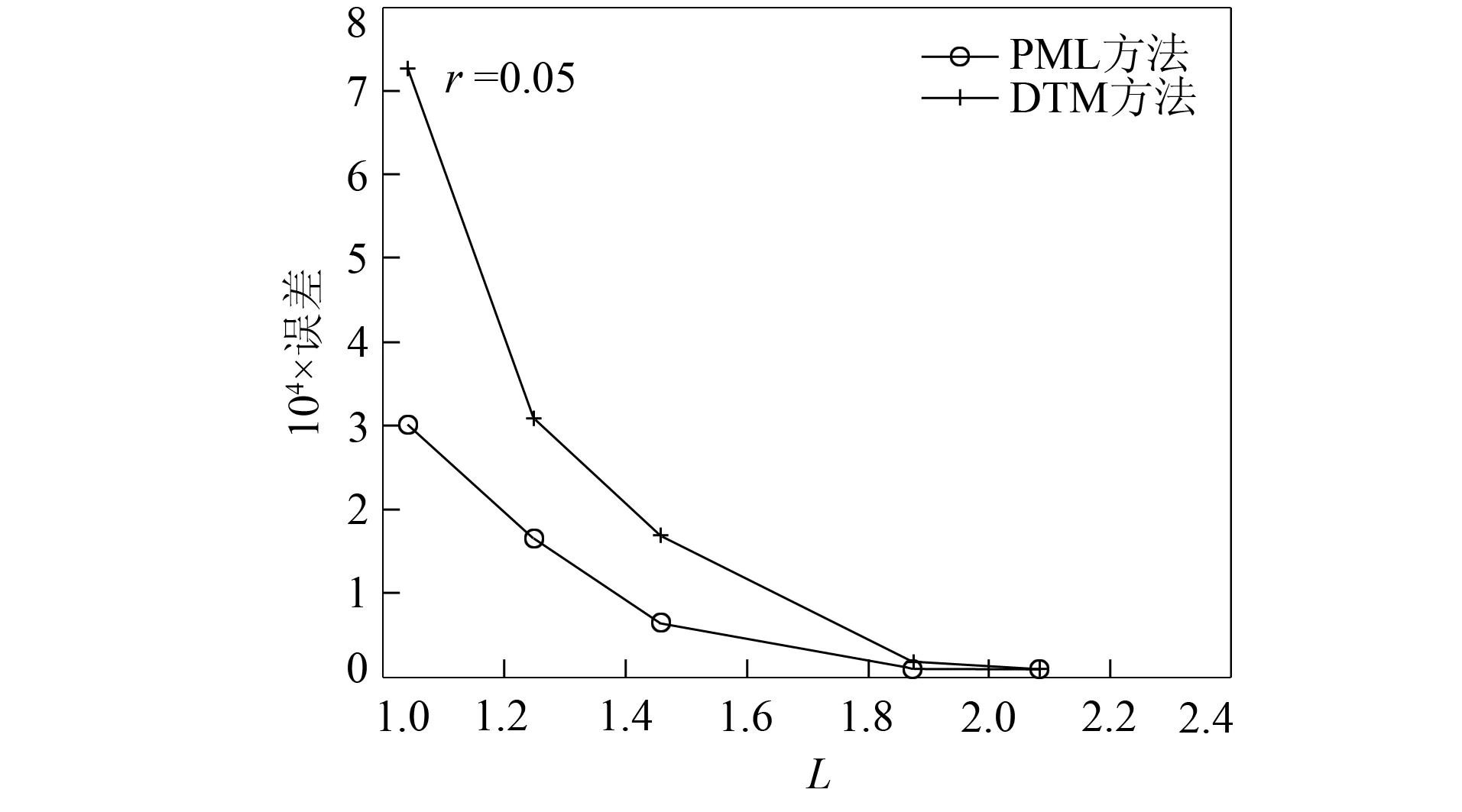
Ω={(x,y)|-L1-δ1 则PML变换可表示为 其中: 于是模型(3)的PML截断形式为 (4) 其中 综上, 通过惩罚法和PML技巧对定价问题进行处理, 本文得到了有界区域上的非线性抛物问题. 为说明PML算法的有效性, 下面介绍远场估计法(DTM), 其主要思想是在无穷远处给出一个合适的截断长度, 以保证截断问题的解与原问题的解足够接近. 不妨设截断区域Ωl=[-l1,l1]×[-l2,l2], 则简化模型(2)的远场近似解Pl(x,y,τ)有以下估计结果: 引理3[12]对固定的时间τ∈(0,T]、 固定的点(x,y)∈2及充分小的数ε>0, 若满足 li≥lmax,i=1,2, 则有 |P(x,y,τ)-Pl(x,y,τ)|≤ε, 其中 图1 空间区域Ω的三角剖分Fig.1 Triangulation of spatial region Ω 考虑非线性微分方程(4). 半隐式有限差分法的主要思想与经典有限差分法相似, 唯一区别是方程中的非线性项采用显式格式, 线性项采用θ-格式. 令时间剖分 Jτ: 0=τ0<τ1<…<τM=T, τm=mΔτ,m=0,1,…,M, 定义差分形式为 从而方程(4)在(xi,yj,τm)处的离散格式为 其中: 下面给出算法的误差估计及所得解Um+1的非负性证明. 为简便, 考虑未加PML技巧的半隐式有限差分方法的误差估计. 证明: 方程(4)在节点(xi,yj,τm)处可表示为 (6) 利用Taylor展开可得: 对于混合交叉项, 由Taylor展开得: 故有 下面给出数值解的非负性证明. 为简便, 对于两个相互独立(ρ=0)标的资产的美式期权定价问题, 考虑应用未加PML技巧的半隐式有限差分法(θ=0)所得解的非负性, 对于其他情形有类似结论. 证明: 当条件ρ=0,θ=0成立时, 方程(5)转化为 其中: a1=-l3+l5;a2=-l2+l4;b=2l2+2l3+1+rΔτ;a3=-l2-l4;a4=-l3-l5; 观察方程的系数和右端, 把所有系数都乘以h2/Δτ, 当h足够小时, 可得 下面通过数值算例验证所给算法的有效性. 考虑一年期的美式多资产看跌期权, 模型(1)中参数分别取为σ1=0.2,σ2=0.3,q1=0.05,q2=0.01,α1=0.6,α2=0.4,θ=0.5,r=0.05, 敲定价格K=1, 惩罚法系数为η=10-2. PML模型中的系数为λ1=λ2=10,β1=β2=3,δ1=δ2=10h. 图2为远场截断方法(DTM)和PML方法的误差关于截断长度L的变化曲线. 由图2可见, PML方法误差更小. 随着截断长度L的减小, PML方法的误差并未随之显著增大, 表明PML方法并非绝对依赖于截断长度,是一种处理无穷区域问题的有效方法. 图3为本文算法在τ=T及截断长度L=0.5lmax时的三维图像. 图2 DTM和PML方法截断长度L的误差曲线Fig.2 Error curves of truncation length Lof DTM and PML methods 图3 本文算法期权价格的三维图像Fig.3 Three-dimensional image of option price of proposed algorithm
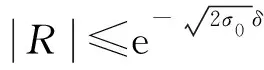
2 半隐式有限差分法

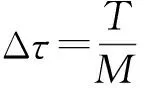


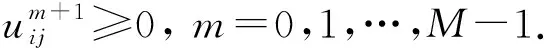
3 数值算例