考虑膝关节转动刚度的二段腿行走步态分析

林彬添，张清文, 范 峰

(1.结构工程灾变与控制教育部重点实验室(哈尔滨工业大学)，哈尔滨 150090；2.土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学)，哈尔滨150090)

倒立摆是模拟人体步态的基本模型.文献[1]采用一个由无质量的线弹簧腿和质点组成的倒立弹簧摆(spring-loaded inverted pendulum, SLIP)来模拟奔跑，见图1(a)；文献[2]采用两条无质量的刚性腿和质点组成的倒立摆来模拟行走；文献[3]将行走和奔跑统一用线弹簧倒立摆进行模拟，见图1(b)，采用这种柔性腿模型的优点是行走双足支撑阶段能够得到很好的模拟；文献[4]进一步研究了线弹簧腿倒立摆抵抗扰动稳定行走的能力，以及模型行走的效率，给出了模拟人体正常行走的合理参数范围.此外，文献[5]在SLIP模型的基础上附加了半圆来考虑行走过程中落脚点的前移，见图1(c)；文献[6]考虑了躯干和髋关节的影响，研究人体行走的姿态控制和稳定性.

这类模型虽然构造简单，但是能够合理地描述人体质心的运动轨迹，其地反力(ground reaction force, GRF)时程具有实测行走荷载时程的“双峰值”特性[3]，同时动力学分析方便，因而被广泛地运用于不同领域，例如，基于倒立弹簧摆抵抗扰动稳定行走的特性，文献[7-8]将其用于设计机器人；医疗领域，文献[9]将其用于人体负重行走研究，预防摔倒；伴随着建筑结构跨度的增大，人体运动荷载导致的结构振动问题逐渐显现出来，文献[10-11]将倒立摆模型与结构动力学模型耦合，分析人与结构的相互作用机理.

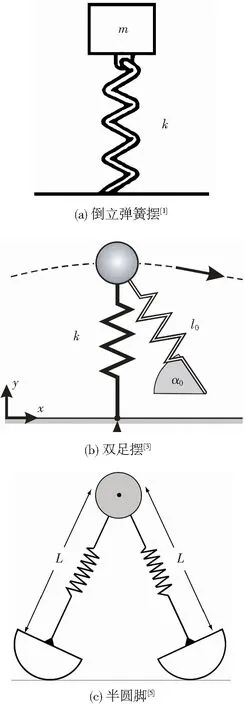
图1 倒立摆模型

值得注意的是，真实人体的腿部并不是理想的线弹簧，而是由多个肢体和关节构成的复杂机构[12]，极度的简化也为模型的实验验证及参数标定带来了困难.采用刚性杆件代表肢体，通过具有转动刚度的关节进行连接，同样具有柔性腿特性，进而能够模拟双足支撑阶段.为了分析腿部构造对倒立摆行走步态的影响，本文考虑了一种由含膝关节的二段腿和质点组成的倒立摆模型.本文首先确定了膝关节的刚度和初始角度对腿部力学特性(腿部反力与腿长关系)的影响，然后建立了模型运动的控制方程和仿真模型，采用庞加莱映射和牛顿迭代法求得了模型周期性行走的步态结果，分析了模型参数对行走步态的影响.

1 二段腿倒立摆模型

本文采用的二段腿模型见图2，人体质量为m，集中在质心(center of mass, CoM)，质心坐标记为(xm,ym)，由两条无质量的腿进行支承，腿部包含两个刚性肢体，代表小腿和大腿，其中小腿长度为l1，大腿长度为l2，通过具有转动刚度k的膝关节连接在一起，定义图示由大腿延长线转向小腿所成的锐角为膝关节角，用θ表示，膝关节内力矩为0的角度定义为膝关节初始角度，用θ0表示，假定腿部在支撑相与地面铰接，忽略落脚点的前移与脚部相对地面的滑动，落脚点的水平坐标记为di，下标i表示落脚点对应的步数.

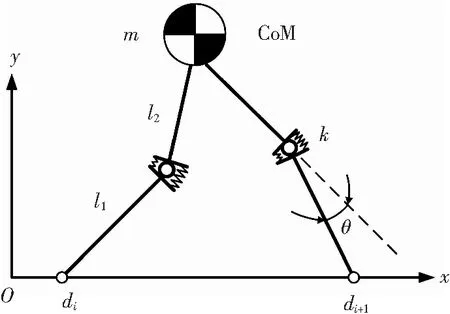
图2 二段腿模型

根据步态分析领域的定义，两个相邻步态事件之间的行走过程为一个单步(step)[3]，单步过程起点的选取不影响步态的讨论，本文选取竖直腿摆向(vertical leg orientation, VLO)事件[4]作为单步过程的起点，假定此时模型处于单足支撑阶段且质心位于落脚点竖直上方，模型行走的第i个单步见图3.

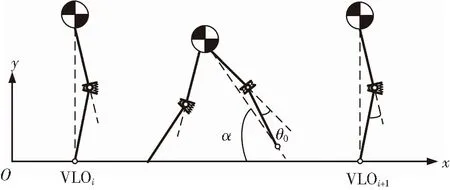
图3 单步过程示意

两个相间步态事件之间的行走过程为一个跨步(stride)，例如，同侧腿的两个相邻VLO事件之间的行走过程，可知一个跨步包含两个单步.由于摆动腿没有质量，对质心运动没有影响，图示没有将其画出；质心由图示位置向前运动，摆动腿始终与地面保持恒定的冲击角α，当质心与假定落脚点的距离恰好为腿初始长度时，摆动腿触地，进入双足支撑阶段，两个相邻落脚点间的水平距离即为步长；当后支撑腿的反力减小为0时，后支撑腿离地，再次进入单足支撑阶段，直到质心来到下一个落脚点竖直上方，即VLOi+1，代表模型完成了一个单步过程.

对质心进行受力分析，见图4，因为模型的腿部没有质量，可以等效为一个二力杆，所以腿部受到的两个反力必然等值，沿着作用点的连线方向，方向相反.膝关节的内力矩为k(θ-θ0)，由三角形面积相等可得腿反力相对于膝关节的力臂为

(1)

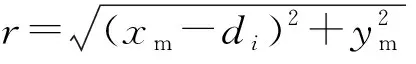
Fh=k(θ-θ0)，

(2)

将式(1)代入式(2)，整理可得腿部的反力大小为

(3)

式中P=k(θ-θ0)/l1l2sinθ为名义腿刚度.

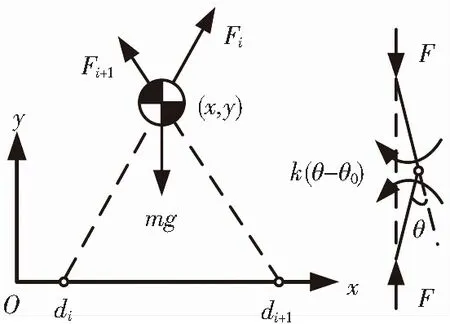
图4 受力分析示意

质心(双足支撑阶段)受到重力mg与腿部作用力Fi和Fi+1，由牛顿第二定律可得：

(4)

(5)

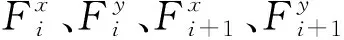
(6)

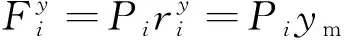
(7)

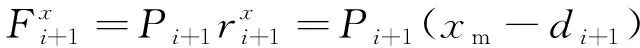
(8)

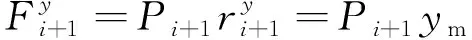
(9)

代入式(4)、(5)，可得质心的运动方程：

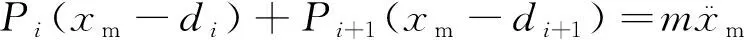
(10)

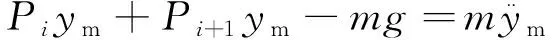
(11)

单足支撑阶段运动方程形式相同，仅保留支撑腿对应项即可.

定义状态向量

模型的状态方程为

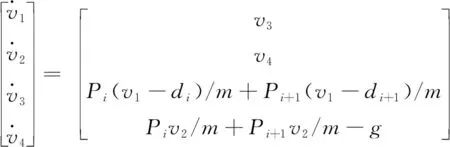
(12)

状态向量的维数为4，由于模型是一个保守系统，机械能守恒，施加一个约束条件，机械能给定为E0，采用状态空间分析方法[13]，根据VLO事件建立庞加莱映射[4]，系统独立的变量维数缩减为2，独立变量的选取不影响系统的性质，本文参考文献[4]，选取的独立变量为VLOi时刻的质心高度y0和速度方向角β，见图5.

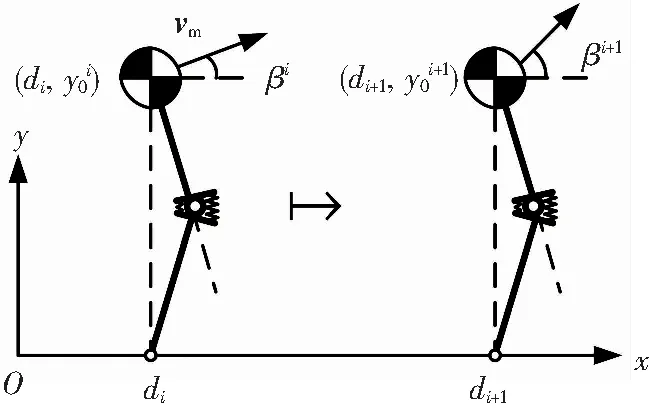
图5 庞加莱映射示意

由此建立的庞加莱映射为

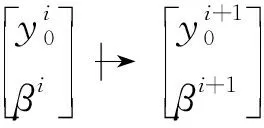
(13)

庞加莱映射的不动点[13]即为模型的周期性行走步态，本文在MATLAB/SIMULINK环境建立仿真模型，模型框图见图6，模型包括：积分模块、单双足支撑相转换模块和触地离地判定模块3个部分，状态方程的求解采用ode45变步长求解器.采用牛顿迭代法求取了模型不动点，由此得到了模型周期性行走步态结果.

2 二段腿力学特性

为比较二段腿和线弹簧腿的力学特性，绘制腿部受到的反力与腿长的关系曲线，见图7.根据文献[12]可知人体大小腿长度相近，本文取大小腿长度l1、l2均为0.5 m；参考文献[4]中给出了人体正常行走的腿刚度范围(应大于14mg/l0，l0为线弹簧原长，本文取m=80 kg)，选用原长为1.0 m，线刚度为12 kN·m-1的线弹簧作为对照组，由公式(1)可知腿内力正比于膝关节转动刚度k，取膝关节腿刚度k=400 Nm·rad-1；进而可分析膝关节初始角度对二段腿动力特性的影响，见图7的反力-腿长曲线.

根据文献[14]可知，人体正常行走时，质心的竖直位移幅值为0.091 m，仿真过程中发现模型的腿长度大于0.9 m，故本文分析的腿长范围为0.9 m到腿初始长度.由图7可知，二段腿受压缩的初期，反力随着变形的增大上升较快，表明二段腿有较大的初始刚度，随着变形的逐渐增大，反力的上升较为缓慢，表明二段腿在变形较大时有柔化现象.分析可知，随着变形的增大，反力的力臂变长，由式(2)可得，单位膝关节内力矩可以抵抗的反力减小，因而二段腿有受力柔化特性.在本文的分析范围内，膝关节初始角度的增大导致反力-腿长曲线的左移，相同腿长条件下，膝关节初始角度大的二段腿内力矩较小，故能够抵抗的反力较小.

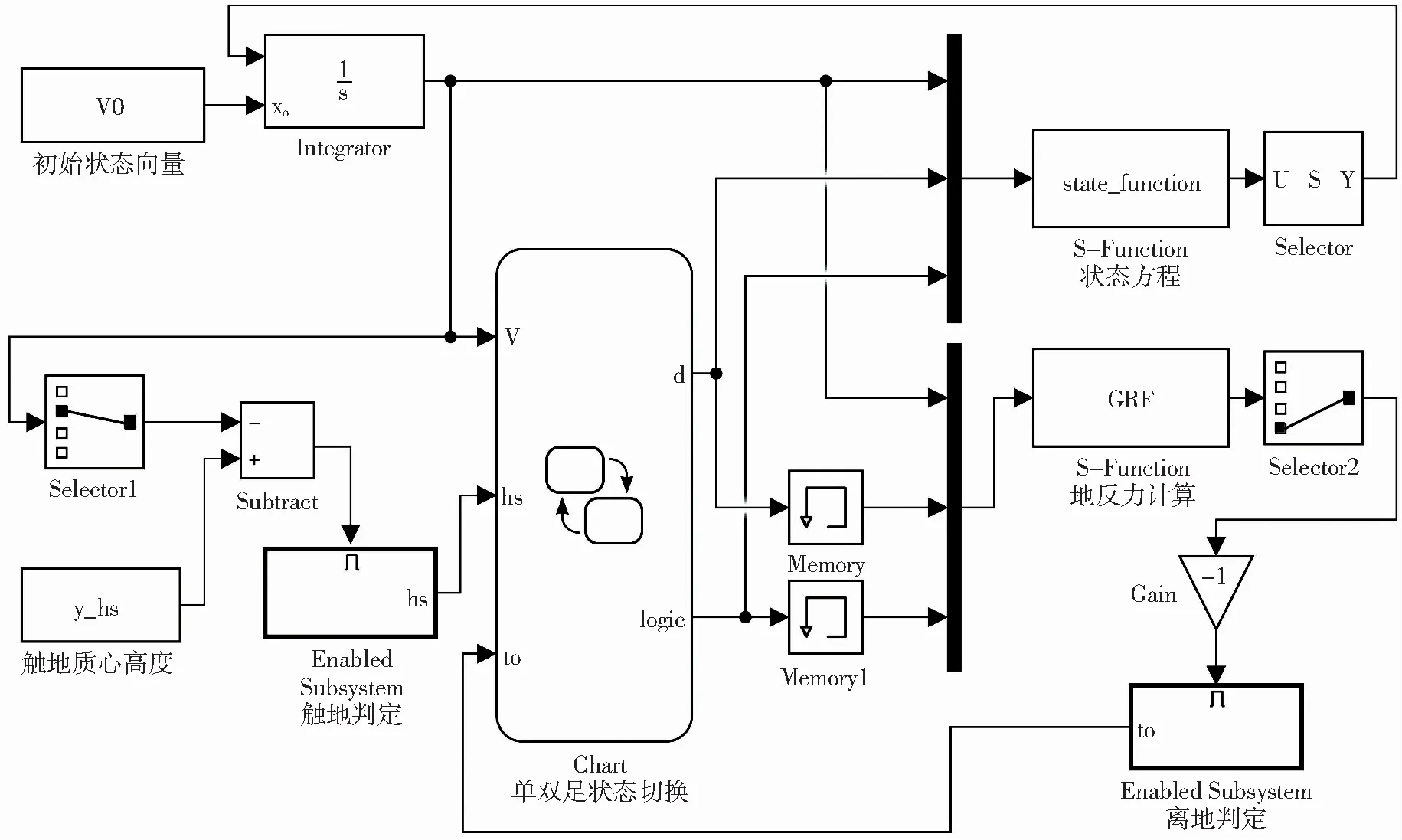
图6 SIMULINK模型

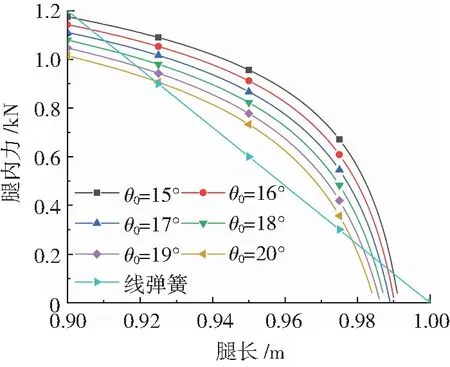
图7 二段腿力学特性

3 二段腿模型行走步态

3.1 机械能的影响

与线弹簧模型类似，二段腿模型能够在较大的冲击角范围内实现周期性的行走步态.图8为膝关节转动刚度k=400 Nm·rad-1，初始角度θ0=20°的二段腿模型，在不同机械能E0下周期性步态的分布情况.图8曲线上的每个点均对应一个周期性的步态结果，由图8可知，二段腿模型能够实现对称性和非对称性(地反力时程曲线的形态，见图9)两类周期性步态，其中，对称性步态在VLO时刻的质心速度方向角均为0，而非对称性步态不为0，见图8(c).α-β曲线与β=0的交点为一个对称性步态，随着机械能的减小，其冲击角α逐渐增大，由该对称步态向两边发展得到的非对称步态，其VLO时刻的质心高度y0均逐渐减小，见图8(b).观察图8(c)可知，机械能较小的非对称性步态冲击角较大，因而摆动腿触地时质心的高度较大，同时由图8(b)可知，VLO时刻质心的高度y0随机械能减小而降低，当机械能进一步减小，VLO时刻模型处于单足支撑阶段的假定将不能满足，不能求得非对称性步态，本文得到的非对称性步态结果可行域为E0不小于790 J.观察图8(a)可知，对称性步态在α-y0坐标上存在两个分支，当机械能E0=820 J时，两个分支分别位于左上角和右下角，随着机械能E0的减小，曲线的分布形式发生了改变，例如，当机械能E0=800 J时，两分支分别位于图示左下角和右上角.

图9展示了图8所示步态A至F的一跨步地反力时程曲线.由图9(b)可知，该分支上的步态，其地反力时程与实测地反力时程不同，仅有一个峰值；由图9(d)可知，该分支的步态结果步频较高，且双足支撑阶段时间占步行周期较大比例，行走效率较低[4]，故后续不再讨论这两种步态.图9(a)、(c)、(e)和(f)具有人体行走地反力的“双峰值”特性，通常来说，人体行走的落步荷载时程是非对称的，其第二个峰值稍小于第一个峰值[15-16]，步态F所在分支更接近于真实行走落步荷载.

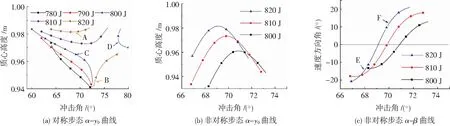
图8 机械能对步态分布的影响

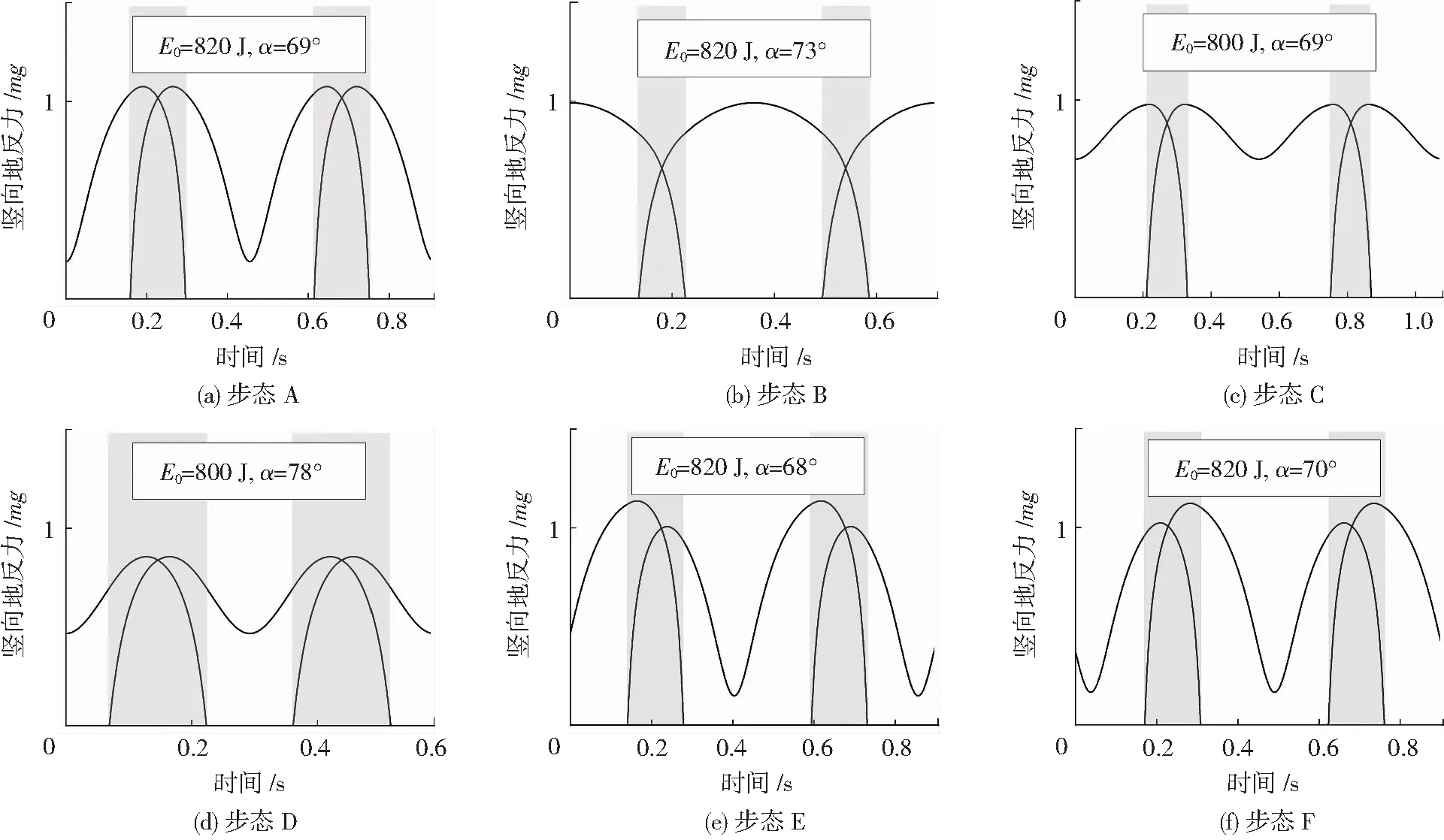
图9 竖向地反力时程

对比图9(a)、(c)可知，机械能E0的降低将导致地反力时程峰值减小，同时峰值之间的低谷值将增大.为分析机械能对步态参数，包括步频、步长和平均步速的影响，以步态A为对照组，仅改变机械能E0，各步态的步态参数见表1，由表1可知，机械能的减小将导致步频降低，步长增大，平均步速减小.提高平均步速最有效的方式为增加能量输入，这与线弹簧模型结论一致[3].

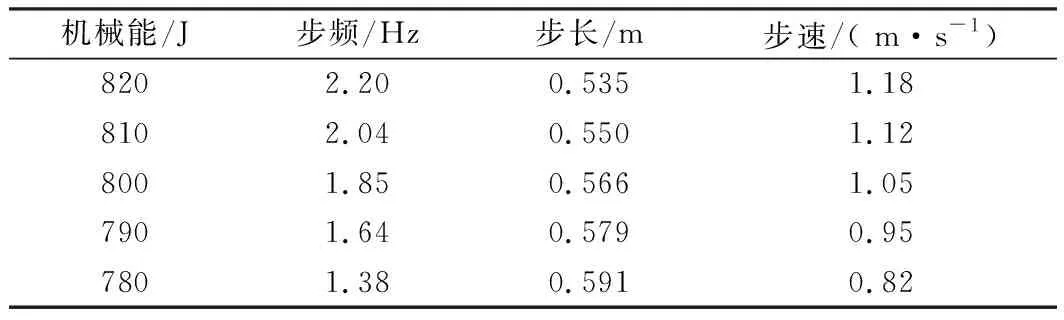
表1 机械能对步态参数的影响

3.2 冲击角的影响

为分析冲击角对模型步态参数的影响，表2列举了步态A及其邻近步态的步态参数.由表2可知，随着冲击角的增大，对称性步态的步频逐渐提高，步长逐渐减小，平均步速则稍有降低.文献[17]指出人体正常行走的步频范围为1.6 Hz到2.4 Hz，结合表1、2可知，本文展示的步频范围为1.38 Hz到2.43 Hz，可见二段腿模型在给定参数范围下能够较好地覆盖人体正常行走的步频区间.

表3列举了非对称性步态F及其邻近步态的步态参数，由表3可知，在本文分析的冲击角范围内，非对称性步态的步态参数对于冲击角的变化不敏感.分析可知，对称性步态处于VLO状态时速度方向角为0，冲击角控制摆动腿的触地判定，直接影响步态参数；非对称性步态处于VLO状态时速度方向角不为0，摆动腿的触地判定由冲击角和速度方向角共同决定，步态参数基本不变，然而地反力两个峰值的大小关系发生了变化，见图9(e)、(f).

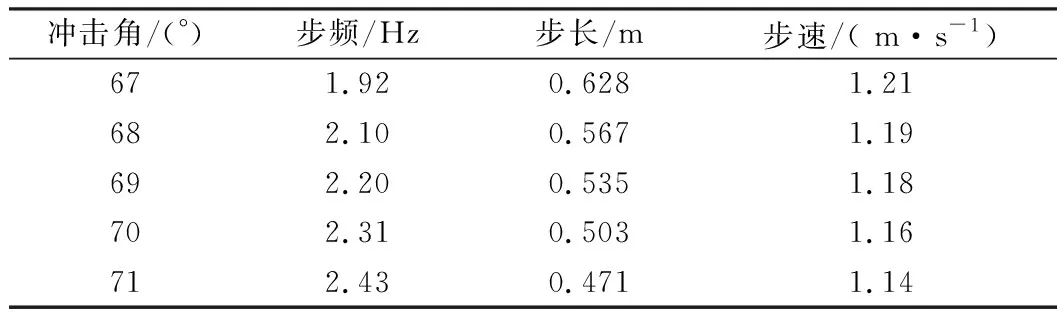
表2 冲击角对步态参数的影响(对称步态)

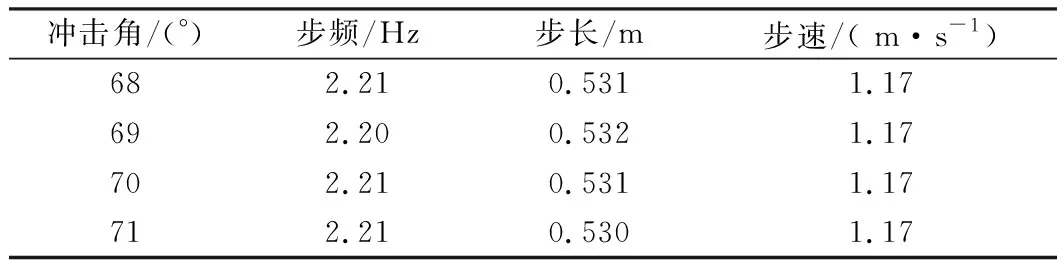
表3 冲击角对步态参数的影响(非对称步态)

3.3 膝关节初始角度的影响

为分析膝关节初始角度对步态分布的影响，图10展示了机械能E0=820 J，膝关节转动刚度k=400 Nm·rad-1条件下，不同膝关节初始角度的二段腿模型的步态分布情况.由图10(a)可知，对于对称性步态，以步态A所在分支为参考，随着初始角度的减小，步态分布曲线右移，表明冲击角增大；对于非对称性步态，以步态F所在分支为参考，随着初始角度的减小，步态分布曲线右移.由此可见，膝关节初始角度较小的二段腿模型产生的步态具有较大的冲击角.

表4分析了膝关节初始角度对步态参数的影响，以步态A为对照组，减小膝关节初始角度将导致步频降低，步长增大，然而平均行走速度的变化很小.由图7可知，在本文讨论的参数范围内，膝关节初始角度的减小导致曲线右移，其效果近似于腿长变长，在冲击角相同的条件下，如图10(a)所示，VLO时刻的质心高度增大，VLO到摆动腿触地耗时变长，因而步频降低，步长增大.

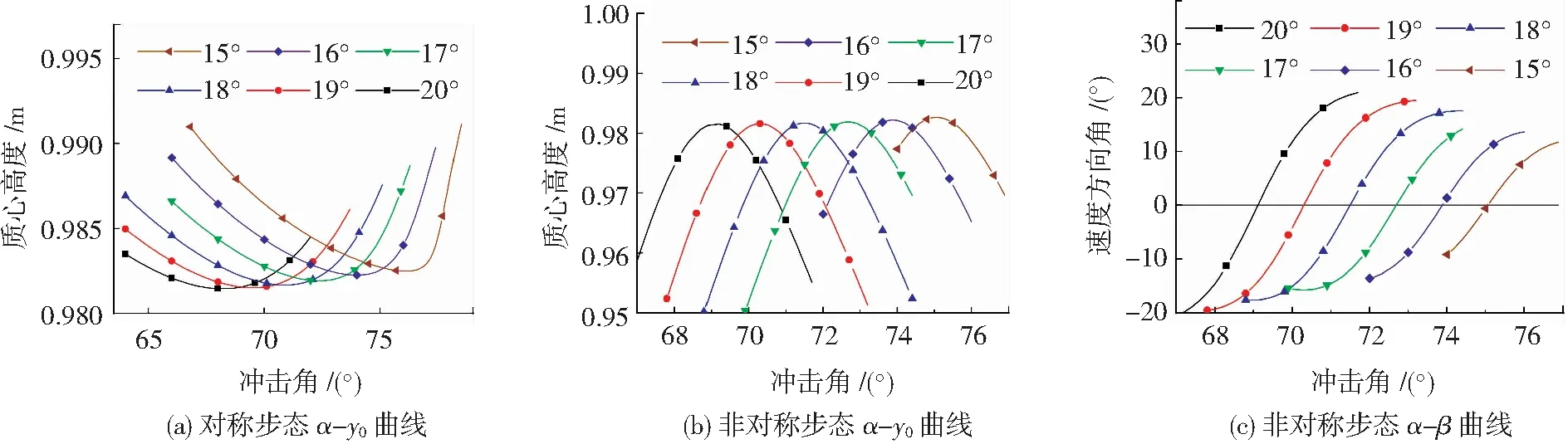
图10 膝关节初始角度对步态分布的影响

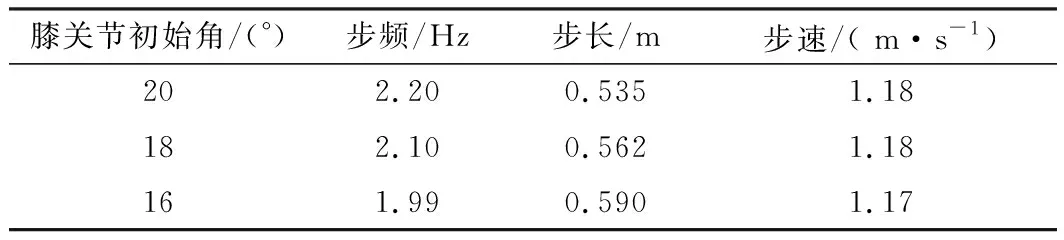
表4 膝关节初始角度对步态参数的影响

3.4 膝关节转动刚度的影响

为分析膝关节初始角度对步态分布的影响，图11展示了机械能E0=820 J，膝关节初始角度θ0=20°条件下，不同膝关节转动刚度的二段腿模型的步态分布情况.由图11(a)可知，对于对称性步态，以步态A所在分支为参考，随着膝关节转动刚度的增大，步态分布曲线对应的冲击角区间扩大，表明刚度更大的腿能够在更大的冲击角范围内实现周期性行走；对于非对称性步态，以步态F所在分支为参考，随着膝关节转动刚度的增大，步态分布曲线右移.由此可见，膝关节转动刚度较大的二段腿模型产生的非对称性步态具有较大的冲击角.

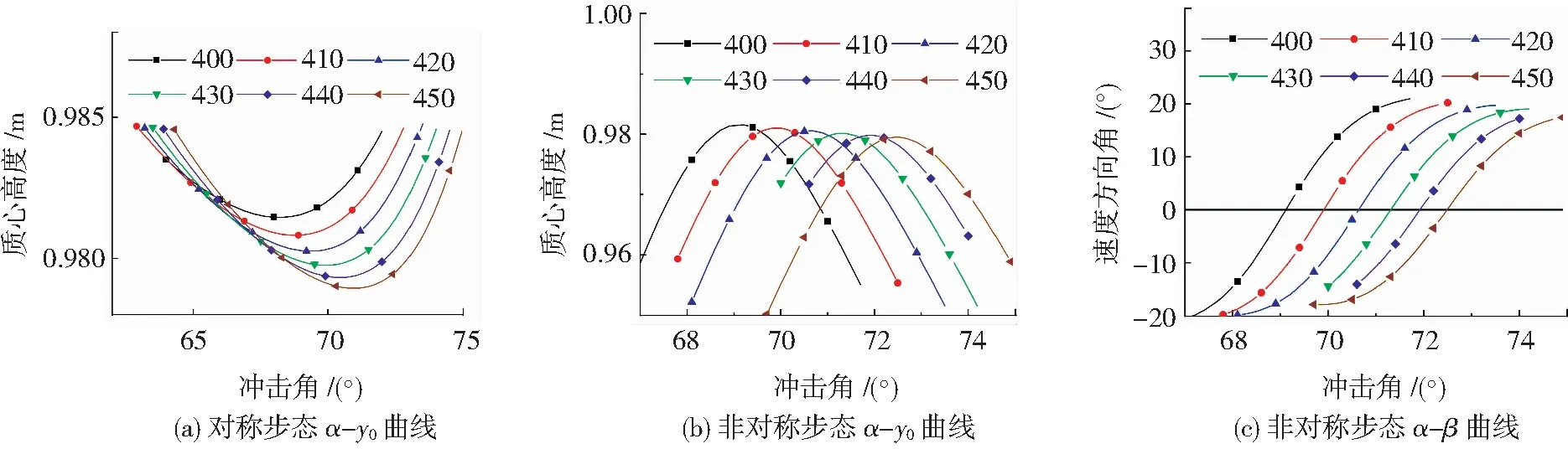
图11 膝关节转动刚度对步态分布的影响

表5分析了膝关节转动刚度对步态参数的影响，以步态A为对照组，增大膝关节转动刚度将导致步频小幅度降低，步长小幅度增大，平均行走速度稍有增大.由图11(a)可知，冲击角相同的条件下，虽然刚度更大的二段腿VLO时刻的质心高度较低，但是腿部对质心竖向的支撑作用更强，从VLO到摆动腿触地耗时依然更长，其步频更低.

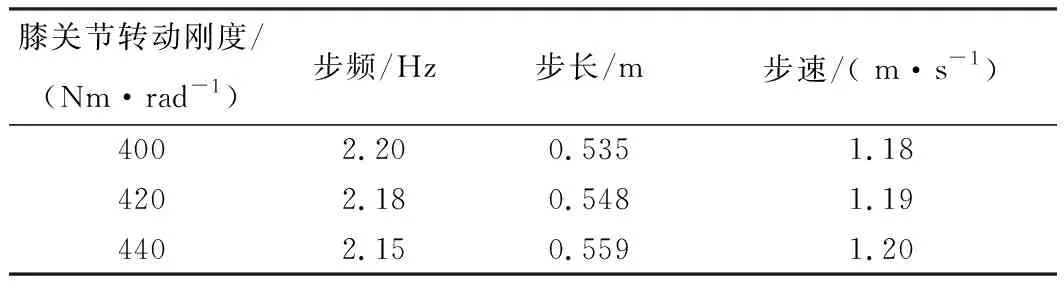
表5 膝关节转动刚度对步态参数的影响

4 结 论

本文对一种由膝关节连接的二段腿模型开展了建模分析，得到的主要结论如下：

1) 带膝关节的二段腿有较大的初始刚度，随着变形的增大，刚度逐渐降低，即存在受力柔化现象.

2) 二段腿模型能够在一定的参数范围内实现多种形式的周期性步态，可分为对称性和非对称性两大类.

3) 模型参数对步态参数的影响可总结为：增大模型的机械能，平均行走速度提升最显著；冲击角对对称性步态的步态参数影响显著，非对称性步态的步态参数对冲击角不敏感；减小二段腿的膝关节初始角度，改变步态的频率和步长关系，而平均行走步速变化很小；膝关节转动刚度增大将小幅度降低步频，增大步长和平均行走速度.

4) 二段腿模型能够很好地模拟人体行走地反力的“双峰值”特性，给定合理的参数组合，模型能够覆盖人体正常行走的步频区间.

可见二段腿模型同样具有柔性腿特征，能够有效模拟人体行走双足支撑阶段，重现地反力时程的双峰特性，同时，其构造更加接近于真实人体，参数物理意义明确，为模型的实验验证及参数标定打下了基础.进一步的人体行走试验有待开展，测量人体运动学及动力学参数，探讨简化模型的合理性.