铁路56 m简支箱梁的碳化寿命预测

张若男 蔺鹏臻 保琛 王雲一

（1.兰州交通大学甘肃省道路桥梁与地下工程重点实验室，兰州 730070；2.兰州交通大学土木工程学院，兰州 730070）

碳化是影响钢筋混凝土结构耐久性能的重要因素之一。碳化作用就是空气中的CO2不断侵入混凝土，与混凝土中的碱性物质发生反应，使混凝土内部PH 值降低，钢筋表面的钝化膜逐渐被破坏［1］，引起钢筋锈蚀膨胀，降低构件的承载能力，最终危及结构安全。

对桥梁结构进行碳化寿命预测，可以科学推测桥梁的正常运营年限，充分挖掘桥梁的使用潜力。文献［2］以大量工程实践为背景，采用可靠度理论建立碳化寿命预测模型。文献［3］提出了混凝土碳化深度的有限元分析，提供了从微观角度分析碳化过程的研究思路。文献［4］介绍了一种混凝土构件多尺度分析的寿命预测模型，为外部钢筋的寿命估算提供了新的解决方案。文献［5］提出了一种钢筋混凝土结构在钢筋腐蚀方面的耐久性和使用寿命的评估方法。

一个好的碳化模型，不仅要符合碳化的物理化学过程，要有理论基础，而且要便于工程应用，能将理论分析与工程实际有效结合［2］。本文首先介绍了基于可靠度寿命预测的牛荻涛模型和基于热传导理论的碳化寿命预测方法，然后通过ANSYS热分析模块模拟碳化过程并与试验实测值比较，验证以热传导理论为依据的碳化寿命预测方法的科学性与可行性。最后，分别用这2 种方式预测银川机场黄河特大桥56 m 简支箱梁桥段的碳化寿命。

1 混凝土碳化寿命预测方法

结构的使用寿命或耐久性年限的定义为建筑结构在正常使用和正常维护条件下，仍然具有其预定使用功能的时间［6］。钢筋锈蚀是影响钢筋混凝土结构耐久性的主要因素之一。因此，混凝土碳化寿命允许指标以钢筋表面不出现锈迹作为标志。牛荻涛模型以钢筋表面开始锈蚀为达到碳化寿命的标志［2］；基于热传导理论来模拟碳化过程的碳化寿命计算方法以钢筋表面CO2浓度达到一定值为标志。

1.1 基于可靠度的碳化寿命预测方法［2］

碳化过程是个复杂的随机过程，具有很强的变异性。从混凝土碳化过程及影响因素可知，混凝土碳化深度产生变异的原因来自混凝土本身与环境的变异性。牛荻涛提出的预测混凝土碳化寿命的多系数随机模型以混凝土质量与环境条件因素为主，同时考虑碳化位置（角部与非角部）、应力状态（受拉或受压）、养护条件等影响因素。这些因素在自然条件下是随机变量，并服从正态分布。因此，选用的混凝土随机碳化寿命准则Ωc可以表示为

式中：c为混凝土保护层厚度；X0为碳化残量；X（t）为混凝土碳化深度，是关于时间t的变量。

碳化残量X0的计算公式为

式中：H为环境相对湿度；fcu，k为混凝土抗压强度标准值。

碳化深度X（t）的计算公式为

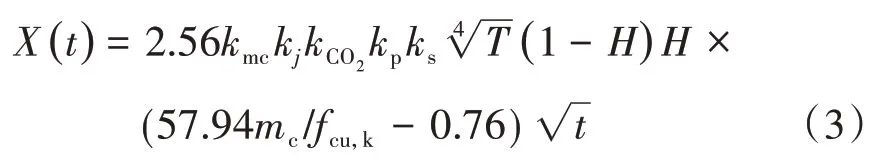
式中：kmc为计算模式不定性随机变量，取0.996；kj为角部修正系数，角部取1.4，非角部取1.0；kCO2为CO2浓度影响系数；kp为浇筑面修正系数，取1.2；ks为应力影响系数，混凝土受压时取1.0，受拉时取1.1；T为气体温度（环境温度）；mc为混凝土立方体抗压强度平均值与标准值之比。

钢筋发生锈蚀的失效概率pfc(t)及相应的碳化耐久度pDC(t)、可靠度指标βc分别表示为

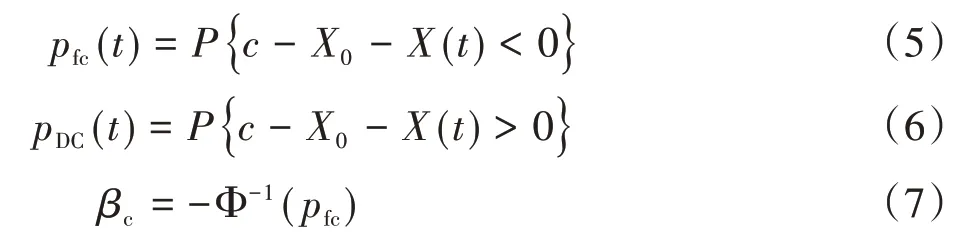
可靠度指标的选取要综合考虑桥梁的重要程度与技术状况。文献［7］从国内外规范的校准、工程实测的论证、结构的重要程度等方面综合讨论，提出基于碳化寿命耐久性设计的目标可靠度指标及对应的失效概率，见表1。

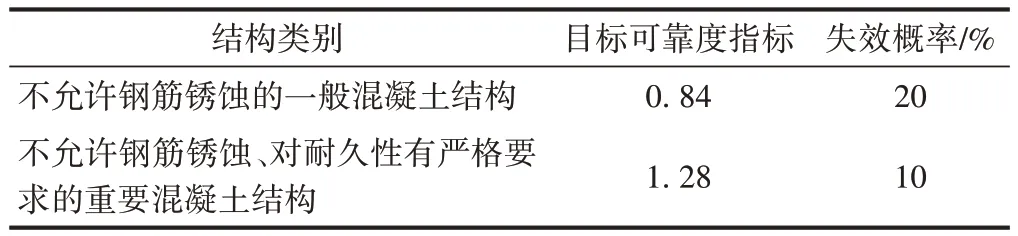
表1 基于碳化寿命耐久性设计的目标可靠度指标

1.2 基于热传导理论的碳化寿命预测方法

碳化过程实质上就是CO2从混凝土表面进入混凝土内部的扩散过程。取碳化区域内一个微元体，基于质量守恒定律，考虑微元体内碳化过程前后CO2含量，并结合Fick第一定律，得到碳化控制方程

式中：C为浓度变量，是时间和方位变量的函数；DC为碳化扩散系数；Vr为碳化反应速度。

碳化控制方程与热传导方程从数学形式上完全一致，但方程中各变量的含义不同。ANSYS 中的热分析问题正是通过数值模拟方法对热传导微分方程及其相关边界条件编写程序进行有限元求解。因此，可以用碳化控制方程中的主要参数DC和Vr替换热传导方程中相应的参数并限定边界条件来模拟碳化过程。

通常，环境中CO2浓度为体积百分比浓度。为便于混凝土结构内碳化有限元分析，依据理想气体状态方程，将CO2体积百分比浓度转化为质量浓度C0，即

式中：PCO2为气体分压，常压下取101 325CV，其中CV为CO2体积百分比浓度；V为气体体积，可取 1 m3；R为理想气体常数，取8.314 J/（mol·K）；mCO2为CO2的摩尔质量，取44 g/mol。

本文以保护层处的混凝土完全碳化作为基于热传导理论推断碳化寿命的判断标准。混凝土结构碳化程度可用单位体积混凝土完全碳化消耗掉的CO2质量Cr，max表征［8］。

式中：Z为单位体积混凝土的水泥用量，kg；[ ]CaO 为CaO的质量百分比，通常取64%。

通过APDL 编程，在ANSYS 中输入碳化扩散系数、碳化反应速度、碳化时间、时间步长，限定边界条件C0，输出结果为任意时刻各节点的CO2含量。随着时间的推移，当保护层处混凝土吸收的CO2达到完全碳化所要消耗的量时，认为结构已达到碳化寿命所约定的使用年限。

1.2.1 碳化控制方程关键参数计算公式

参数DC及Vr对碳化控制方程的求解至关重要。

碳化扩散系数DC的计算公式为［9-11］

式中：DC，0为标准状态下的 CO2扩散系数，DC，0= 8 ×10-7(Q- 0.34)(1-Href)2.2，其中Q为混凝土的水灰比，Href为混凝土内的参照湿度；F（1T）为温度对DC的影响其中E为 1 mol 的 CO2反应消耗掉的能量（取21 800 J/mol），Tref为测定DC，0时的平均温度；F（2H）为湿度对DC的影响，F2(H)=(1-H)2.5。

碳化反应速度Vr的计算公式为［9-11］

式中：V0为标准状态下的碳化反应速率，取2.8×10-7（s·mol）-1；f1（T）为温度对Vr的影响，f1(T)= e-E0/(RT)，其中E0为碳化活化能，不同文献的取值差异较大，一般取14.47～91.52 kJ/mol；f2（H）为湿度对Vr的影响，当0 ≤H＜ 0.5 时取 0，0.5 ≤H＜ 0.9 时取 2.5（H- 0.5），0.9 ≤H≤ 1时取1。

1.2.2 基于热传导理论碳化模型的校验

文献［12］制作了4 组箱梁，按照4 种试验工况进行了碳化试验，经一段时间后测得各部位的碳化深度。试验中环境温度为20 ℃，湿度为68%，水灰比为0.35，立方体抗压强度标准值为30 MPa。工况1 和工况3 的CO2的浓度为14%，工况2 和工况4 为28%。工况1和工况2的反应时间为10 d，工况3和工况4为20 d。

为验证基于热传导理论模拟碳化过程的可行性，本文以文献［12］的4种工况为背景求解碳化深度。步骤为：①选用solid70 单元按试验箱梁的尺寸建立三维几何模型并划分网格；②根据试验条件，利用式（9）、式（11）、式（12），求得箱梁的外周设定CO2初始浓度、碳化扩散系数、碳化反应速度；③定义求解时间和时间子步；④输出结果，即箱梁某一时刻各部位CO2的质量浓度；⑤算得碳化深度。

将文献［12］中碳化深度实测值与本文的ANSYS模拟值进行对比，见表2。可知：ANSYS模拟值与实测值吻合良好；角部位置的碳化深度明显大于非角部位置，约成1.5倍的关系，略大于牛荻涛碳化模型中的角部修正系数（1.4）。这说明采用ANSYS热分析模拟碳化过程是一种较为科学、准确的方法。

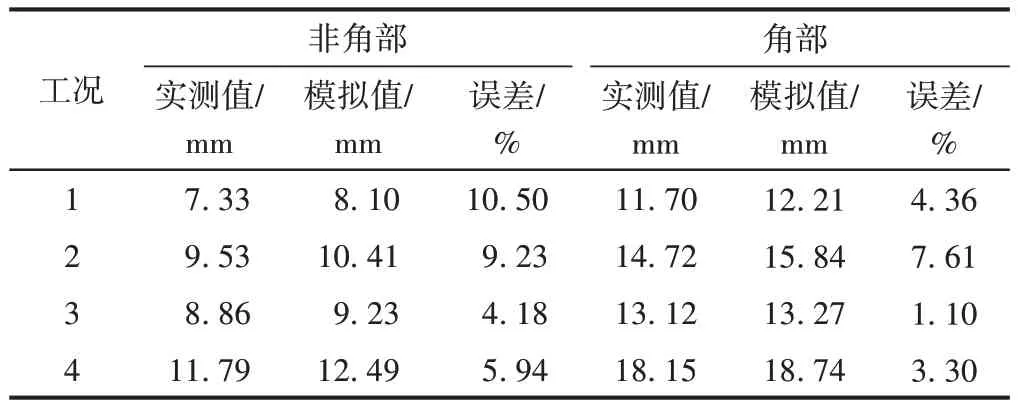
表2 碳化深度的模拟值与实测值对比

2 56 m简支箱梁碳化寿命预测

2.1 工程概况

全长13.8 km 的新建银川机场黄河特大桥位于银川市东南方向，为跨黄河、京藏高速公路及灌溉渠而设。大桥共有13 孔56 m 简支箱梁（以下简称箱梁），横断面见图1。箱梁采用C60 混凝土，混凝土保护层厚度为3.5 cm。大气中的混凝土结构碳化条件较为复杂，为简化计算，自然环境中的温、湿度均取年平均值，分别为8.5 ℃，55%；大桥附近CO2浓度约为0.06%。

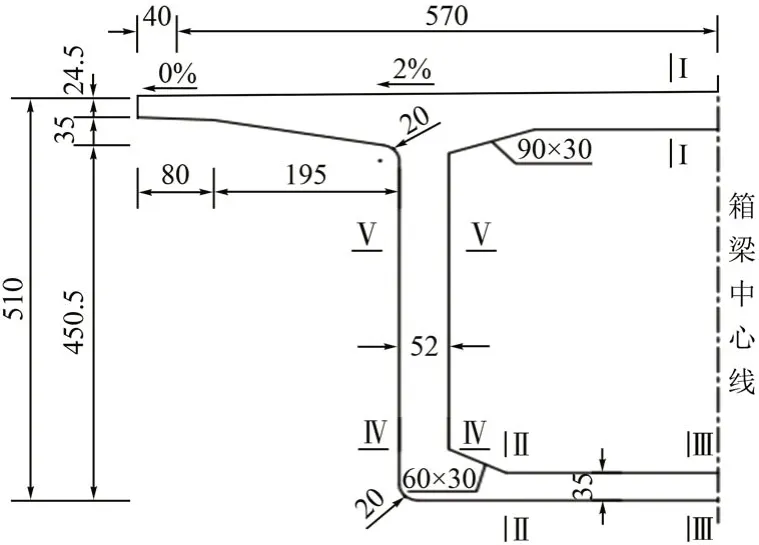
图1 1/2跨中箱梁横断面（单位：cm）

2.2 基于可靠度的牛荻涛模型碳化寿命预测

由于制作尺寸偏差和安装误差，结构构件的各项参数实际值与设计值存在一定偏差。文献［13］给出了实际工程应用时需考虑的构件参数不确定性系数KA。KA服从正态分布，统计参数（平均值μKA和标准差σKA）见表3。

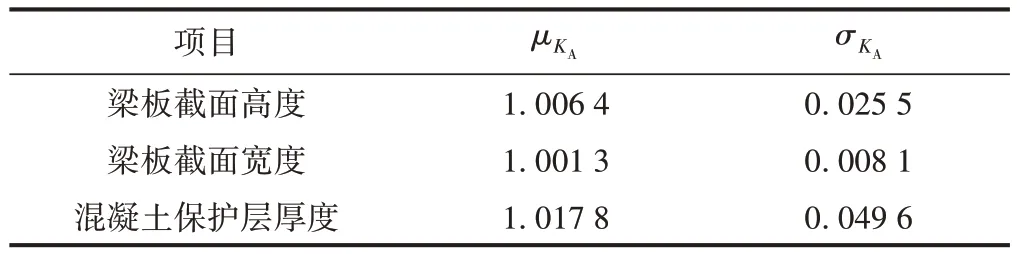
表3 不确定性系数KA的统计参数

根据表3，考虑不确定系数的混凝土保护层厚度c的平均值μc与标准差σc分别为 35.623，1.736 mm。

由式（2）可知，碳化残量X0是关于c的一次函数，也服从正态分布。算得箱梁碳化残量的平均值μX0与标准差σX0分别为22.229，1.097 mm。

碳化深度X（t）的平均值μX(t)与标准差σX(t)的计算公式［2］为

式中：μkmc，σkmc分别为kmc的平均值和标准差；fcu为混凝土抗压强度；σfcu为fcu的标准差。

将碳化深度参数（表4）带入式（13）、式（14），算得箱梁碳化深度的平均值μX(t)与标准差σX(t)分别为

表4 碳化深度参数

56 m 简支箱梁桥段是银川机场黄河特大桥的重要组成部分，是对耐久性有严格要求的重要预应力混凝土结构。钢筋的锈蚀会降低桥体的承载能力以及耐久性能。因此，碳化寿命极限状态的目标可靠度指标的选取以钢筋不发生锈蚀为前提。结合表1，该箱梁碳化寿命极限状态的目标可靠度取1.28，相应的失效概率为10%。利用正态分布的运算性质，该箱梁的碳化寿命为135年。

2.3 基于热传导理论的碳化寿命预测

56 m 简支梁桥为变截面箱梁桥，取跨中箱梁横截面（图1）为几何模型的横截面。考虑到沿桥纵向碳化的一致性，几何模型在纵向取100 cm。建立三维几何模型并划分网格，横断面见图2。

图2 ANSYS几何模型横断面

箱梁单位体积混凝土的水泥用量Z为290 kg。由式（10）算得，单位体积混凝土完全碳化要消耗掉91.69 kg 的CO2。由于混凝土保护层厚3.5 cm，箱梁碳化寿命以箱梁外表面以内3.5 cm 处单位体积混凝土吸收91.69 kg的CO2所需的时间为标准。箱梁暴露在空气中的时间不同，箱梁外表面以内3.5 cm 处的CO2浓度不同，故需同时考虑时间和CO2浓度的变化，求出碳化控制方程的最优解。考虑到标准状态下的碳化反应速率V0以秒计，因此保守地假设每秒消耗掉CO2的质量在数值上等于达到碳化寿命时混凝土内的CO2质量浓度值。

假设箱梁四周及中间矩形孔都为暴露于环境中的外部边界，用CO2的质量浓度分布反映混凝土结构的碳化深度发展情况。

碳化扩散系数DC及碳化反应速度Vr的基本参数见表 5。可以算得DC，0= 1.12×10-7，F1（T）= 0.633，F（2H）=0.136，f（1T）=2.167×10-10，f（2H）=0.125。

表5 碳化扩散系数DC及碳化反应速度Vr的基本参数

由式（9）、式（11）、式（12），算得CO2初始浓度C0=0.114 kg/m3，DC=9.6×10-9，Vr=7.6×10-18。经 ANSYS模拟分析可知，153 年时箱梁的碳化控制方程存在最优解。

考虑到箱梁各部位的碳化程度有所不同，按从上到下、从左到右的顺序以垂直于箱梁表面的Ⅰ⁃Ⅰ，Ⅱ⁃Ⅱ，Ⅲ⁃Ⅲ，Ⅳ⁃Ⅳ，Ⅴ⁃Ⅴ（图1）为指定路径的方向，路径深度以箱梁外表面为起点，将混凝土内部CO2质量质量浓度映射到指定路径上。153 年时各路径CO2质量浓度曲线见图3。可知，对于5 种路径，CO2质量浓度均关于其所在路径的中点位置对称，故可取半分析。CO2质量浓度从箱梁表面到箱梁内部逐渐减小，分为3个阶段：

图3 153年时各路径CO2质量浓度曲线

1）0～8.7 cm段，CO2质量浓度以较大的斜率快速减小至约3×10-9kg/m3。分别对比Ⅱ⁃Ⅱ（角部）与Ⅲ⁃Ⅲ（非角部）、Ⅳ⁃Ⅳ（角部）与Ⅴ⁃Ⅴ（非角部）可知，相同路径深度处角部的CO2质量浓度约为非角部的1.35 倍，且角部的CO2质量浓度减小的速率略大于非角部，这与牛荻涛模型中角部系数的取值吻合。

2）8.7～11.0 cm 段，CO2质量浓度逐渐减小，但减小的幅度及速率明显小于第1 阶段。因为CO2的扩散是由浓度差造成的，而8.7 cm 处的CO2质量浓度量级达到10-9，已经足够小，扩散的速率与幅度也相应减小。

3）11 cm～路径中点，CO2质量浓度基本为0，未被碳化。

综上，离外表面越近，混凝土内部CO2浓度越高，碳化程度越高。

根据图 3，153 年时路径深度为 3.5 cm 处的 CO2浓度为1.9×10-8kg/m3。假设单位体积混凝土每秒吸收的CO2质量为1.9×10-8kg，历经 153 年（4.825×109s）共吸收91.68 kg。因此，可推断该箱梁的碳化寿命为153年。

3 结论

以银川机场黄河特大桥中的56 m 简支箱梁为背景，根据混凝土强度、保护层厚度及环境条件，分别采用基于随机可靠度理论的牛荻涛模型和热传导理论，对桥梁的碳化寿命进行了预测，得出以下结论。

1）通过 APDL 编程，利用 ANSYS 的热分析模块的数据接口输入相应的参数，能实现基于热传导理论的碳化寿命预测。经对比，模拟值与实测值吻合良好，较好地模拟了混凝土的碳化过程，证明了该方法用于碳化寿命预测的可靠性，为碳化寿命的研究分析提供了新的途径。

2）在ANSYS模拟箱梁的碳化过程中发现，箱梁的翼缘与边角处的碳化速率和碳化程度明显高于平直处，是碳化薄弱部位。

3）采用牛荻涛模型和基于热传导理论的碳化寿命预测方法预测56 m 简支箱梁的碳化寿命分别为135 年和153 年。2 种方式得到的碳化寿命虽不同，但都达到了设计基准期的要求。保守预测该56 m 简支箱梁的碳化寿命为135 年，其耐久性能符合正常使用要求。