基于GA-ITA的输油管道泄漏定位研究

华东阳，郭 乔，杨云博，王寿喜

(1.西安石油大学石油工程学院，陕西 西安 710065；2.长庆油田长北作业分公司，陕西 西安 710016)

管道输送是油品的主要输送方式，具有经济实用、安全可靠的特点[1-2]。然而，受老化、腐蚀以及第三方破坏等因素的影响，输油管道泄漏事故时有发生[3-4]。输油管道一旦发生泄漏，不仅会污染环境[5]，给当地人民的生命和财产带来严重威胁[6-8]，更会波及到下游油气市场，影响国家的石油战略安全，造成难以估量的后果。因此，当输油管道泄漏工况发生时，快速、精准地确定泄漏位置对于降低事故损失，确保管道安全运行具有重要意义。

基于管道泄漏模型的泄漏检测方法[9-12]以流体动力学模型为基础建立仿真模型，分析节点处流量、压力等参数及其随时间的变化趋势，即可实现输油管道泄漏检测和定位。其中，反瞬态分析(Inverse Transient Analysis，ITA)法将管道泄漏定位问题转换为最优化问题，根据模拟得到的管道泄漏结果与实际测量值的差值对输油管道泄漏位置进行寻优，即可实现管道泄漏定位。由于ITA方法需要结合优化算法进行求解，因此优化算法的选择成为该方法研究的重点。如Liggett等[13]选用L-M(Levenberg-Marquardt)算法求解，但由于L-M算法属于改进的牛顿法，容易陷入局部最优解；Kapelan等[14]提出采用“GA(遗传算法)+LM”混合算法求解，先通过GA算法寻找全局最优候选解，再利用LM算法从候选解中选出最优解，但两种算法组合会使求解效率降低；陈特欢等[15]提出了基于粒子群算法(PSO)的管道泄漏反问题求解模型，其泄漏定位精度较高，但该算法鲁棒性较差。

针对反瞬态分析法研究过程中存在求解效率低、结果误差较大等问题，本文提出基于GA-ITA的输油管道泄漏定位模型，分别从计算速度和计算精度两方面将GA-ITA模型与PSO-ITA模型、SAA-ITA模型、TS-ITA模型进行对比，并建立不同规模的输油管道仿真泄漏模型，以验证GA-ITA模型的适应性。

1 输油管道泄漏定位原理

1. 1 管道流体动力学模型

流体在管道中流动可视为一元运动[16]，根据质量守恒、动量守恒和能量守恒定律，可建立相应的偏微分方程组[17]如下:

(1)

式中：ρ为流体密度(kg/m3)；t为时间变量(s)；v为流体流速(m/s)；x为沿管长变量(m)；p为流体压力(Pa)；g为重力加速度(m/s2)；λ为摩阻系数，无因次；d为管道内径(m)；Q为单位质量流体向外界放出的热量(J/kg)；z为高程(m)；h为流体的焓(J/kg)；u为流体内能(J/kg)。

做如下假设：①管输过程满流，且管道横截面积不变；②地形无起伏；③流体稳定流动，即流体压力、温度和流速不随时间变化。则公式(1)可转换为下式:

(2)

其中，由热力学关系可知：

(3)

式中：T为流体温度(K)；T0为周围介质温度(K)；K为流体的传热系数；D为管道外径(m)。

公式(2)是常微分方程组，可整理为

(4)

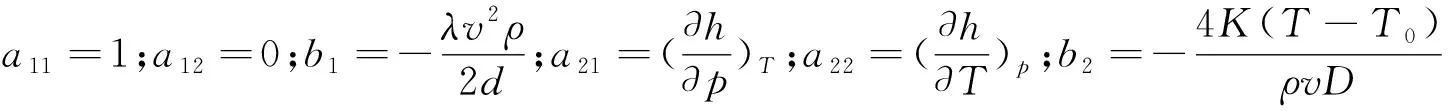
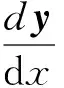
(5)

1.2 ITA法输油管道泄漏定位模型

输油管道发生泄漏后，流体流动仍可由动力学模型描述。输油管道泄漏沿程压力和流速的变化规律见图1。由于管道泄漏后管道内流量减小，因此压降变化趋势减缓；管道内流体密度不发生改变，因此流速仅在泄漏点处发生变化。

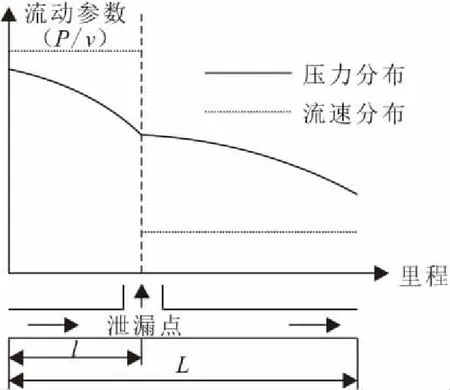
图1 输油管道泄漏后沿程压力和流速分布图Fig.1 Pressure and velocity distribution along the pipeline after the oil pipeline leakage

设管道总长度为L，若泄漏位置与起点间距为l，可根据起点压力P1和起点流量M1计算泄漏点l处压力Pl，进而根据泄漏点处压力Pl和终点流量M2可计算终点压力P2，见下式:

(6)

式中：l为泄漏点与起点间距(m)；P1为起点压力(Pa)；Pl为泄漏点压力(Pa)；L为管道总长度(m)；P2为终点压力(Pa)。

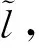
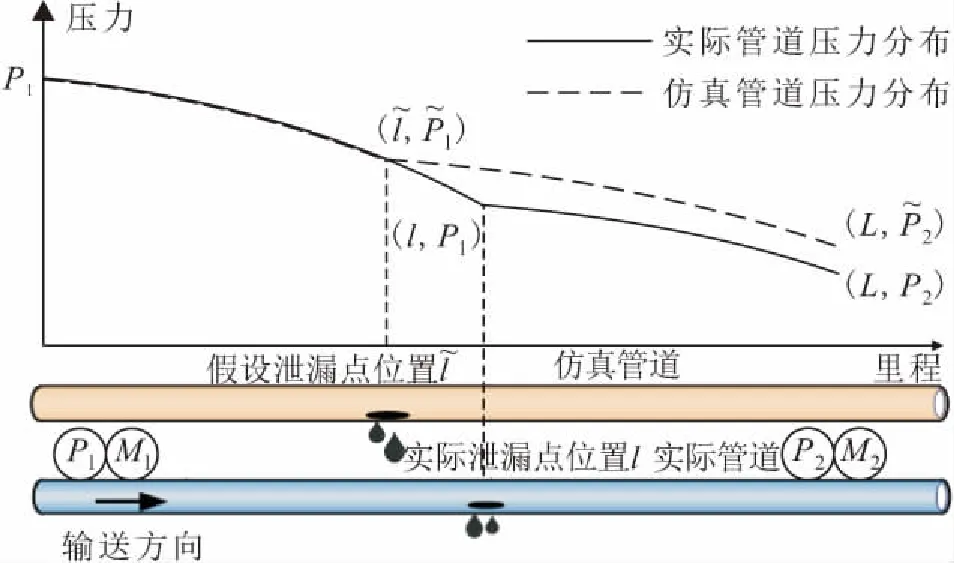
图2 反瞬态分析(ITA)法输油管道泄漏定位原理图Fig.2 Diagram of oil pipeline leakage localization principle of ITA

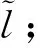
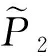
(7)

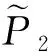
1.3 GA-ITA模型求解

将输油管道泄漏定位问题转换为优化问题后，需要选择合适的优化算法求解目标函数。目前，工程上常用的优化算法有遗传算法(GA)[18-19]、粒子群算法(PSO)[20]、模拟退火算法(SAA)[21]和禁忌搜索算法(TS)[22]。理论上讲，上述4种优化算法均可求解本问题，但不同优化算法由于计算原理不同，计算速度和精度也有差别。

GA是一种借鉴生物进化规律的随机搜索算法，具有适用范围广、鲁棒性强、计算效率高等优点。该算法寻优过程如下：

(1) 种群初始化及编码：本研究设定种群数量为50，种群个体随机生成；采用二进制编码，编码长度为22。

(2) 适应度及被选中概率计算：适应度函数即目标函数，见公式(7)。

(3) 选择：计算每个个体的适应度后，采用轮盘赌法选出适应度高的个体遗传至下一代。其中，个体k被选中概率(Pk)和个体k累计概率(qk)为

(8)

(9)

上式中：fk为个体k的适应度；m为种群总量；Pk为个体k被选中概率；qk为个体k累计概率。

(4) 交叉：通过交叉配对产生新的个体遗传至下一代。本研究选用单点交叉算法，交叉位置随机，交叉概率Pc为0.8。

(5) 变异：改变群体中某些个体的基因，以产生新个体。本研究采用基本位变异法，变异个体及变异基因位随机，变异概率Pm为0.01。

(6) 进化：每次进化重复上述(2)～(5)步骤，产生新的种群；当进化代数达到设置的最大进化代数时，输出进化过程中具有最优适应度个体。本研究设置最大进化代数为200。

基于遗传算法(GA)建立反瞬态分析(ITA)法输油管道泄漏定位模型(即GA-ITA模型)，其泄漏定位流程见图3。

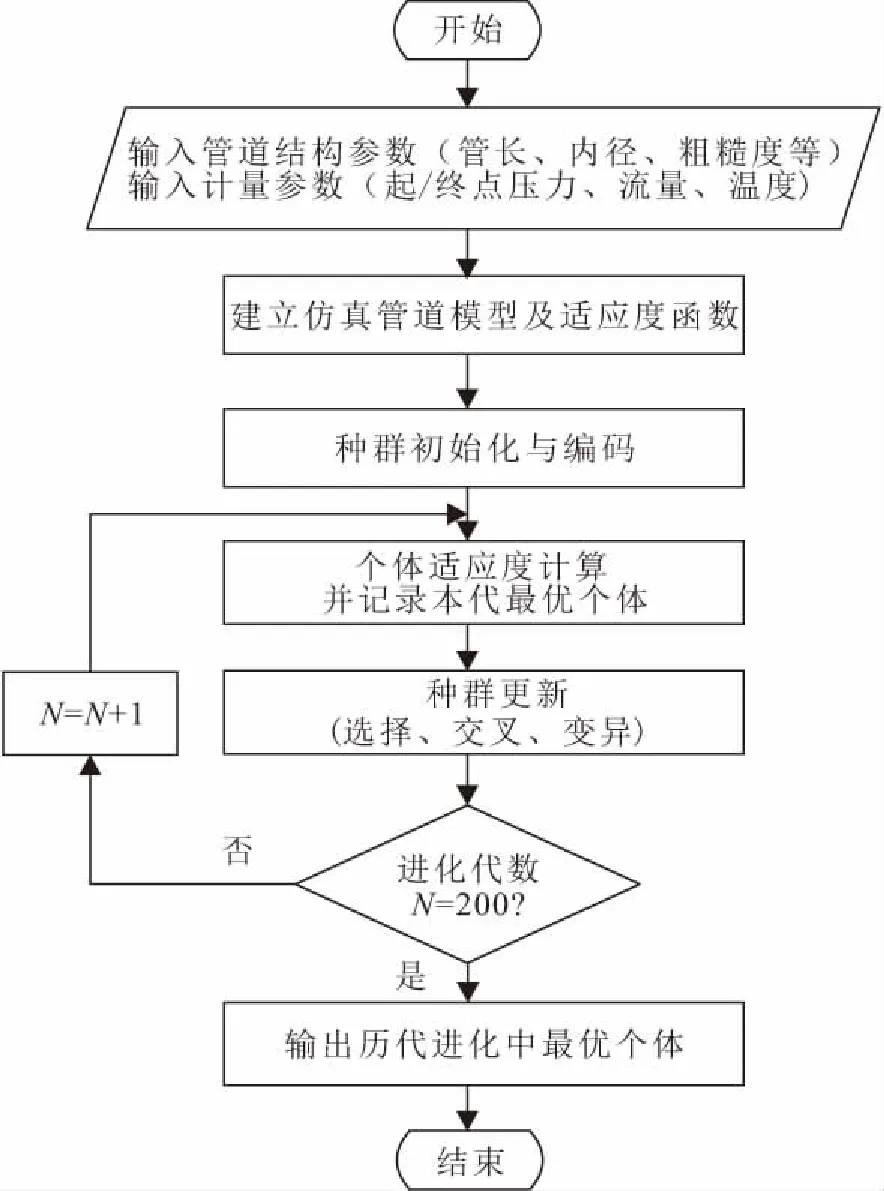
图3 基于GA-ITA模型的输油管道泄漏定位流程图Fig.3 Flow chart of oil pipeline leakage localization based on GA-ITA model

2 实验验证

本研究过程中，首先基于python语言分别建立GA-ITA、PSO-ITA、SAA-ITA、TS-ITA 4种输油管道泄漏定位模型；然后结合室内试验数据求解模型；最后对比不同泄漏定位模型的计算速度与精度。

2. 1 试验数据来源

试验数据来自西安石油大学管网仿真综合实验室，试验设备型号及相关参数见表1。输油管道泄漏试验过程以水作为输送介质，模拟流体常压输送，全程无加热炉；管道沿线设立3个泵站，每个泵站安装两台相同型号调频泵，可通过调节泵的串、并联方式及转速改变管道系统压力和流量。

本次输油管道泄漏试验工艺流程见图4，流体在站1经过加压、计量后进入管道系统，越过站2和站3，在终点处计量后返回储水罐1，储水罐1与储水罐2连通；管道沿线设置两个泄漏点，分别距起点210 m和460 m，管道泄漏率可通过调节阀门开度控制。

表1 试验设备型号及参数

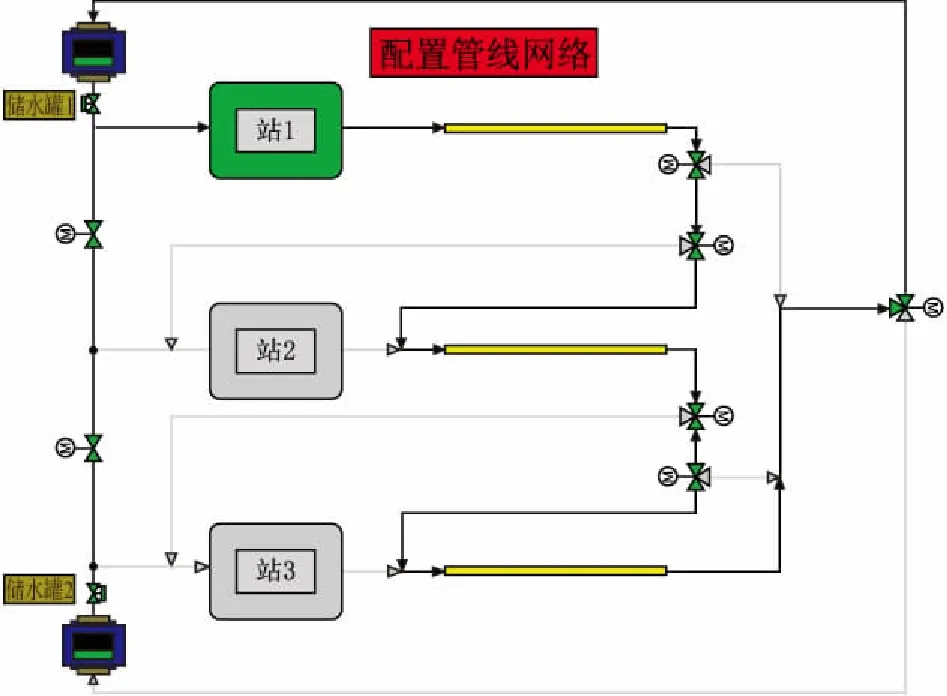
图4 输油管道泄漏试验工艺流程图Fig.4 Flow chart of process of oil pipeline leakage

2. 2 试验结果对比

2.2.1 计算速度对比

输油管道起点、终点的压力和流量(即质量流量)变化情况见图5。本次试验持续时间为150 s，当t=75 s时打开距起点210 m处泄漏阀，阀门开度为40%；当t=85 s后管道泄漏工况稳定。SCADA系统每0.5 s上传1次试验数据，故管道泄漏工况稳定后的试验数据共计130组。受噪声等因素的影响，管道泄漏工况稳定后计量数据仍存在波动。

图5 输油管道泄漏试验数据Fig.5 Test data of oil pipeline leakage

将t=86～90 s的数据(包含10组数据)合并为第1大组数据，t=91～95 s的数据合并为第2大组数据，以此类推，可将泄漏工况稳定后的130组数据合并为13组数据。将13组数据分别代入公式(7)中，并采用不同优化算法求解。不同泄漏定位模型的计算速度对比，见图6。

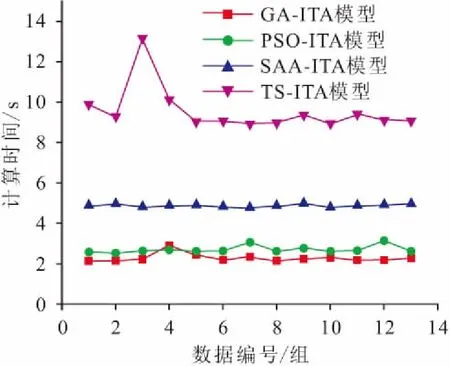
图6 不同泄漏定位模型的计算速度对比Fig.6 Calculation speed comparison of different leakage localizatin models

由图6可见：GA-ITA模型管道泄漏定位耗时最短，约2.3 s即可完成一组数据求解；PSO-ITA模型次之；TS-ITA模型管道泄漏定位耗时最长且计算速度不稳定。

在本研究中，由于室内试验管道规模较小、数据量较少，4种泄漏定位模型的计算速度均能满足实时数据同步要求。但对于长输管道或大型复杂管网系统，不仅实时数据量庞大，而且管道仿真模型更加复杂，势必会影响模型的定位速度；而对于管道泄漏定位问题，更快确定管道泄漏位置能够减少污染、降低损失。因此，在ITA法的实际工程应用中，GA算法在计算速度上更有优势。

2.2.2 计算精度对比

参照上述试验方式，通过改变调频泵的转速以及泄漏阀开度，可模拟不同泄漏工况下4种泄漏定位模型的定位结果。设置泄漏上游压力变化范围为195～300 kPa，泄漏率范围为15%～23%，不同泄漏工况下4种泄漏定位模型的定位结果对比见表2和表3。

由表2和表3可知：不同泄漏工况下，4种泄漏定位模型均能够准确地实现管道泄漏定位；GA-ITA模型管道泄漏定位误差最小，定位误差范围为0.07%～4.67%，TS-ITA模型次之，定位误差范围为0.14%～5.61%，SAA-ITA模型误差波动较大，定位误差范围为0.73%～6.93%，证明GA算法更适用于本问题的求解。

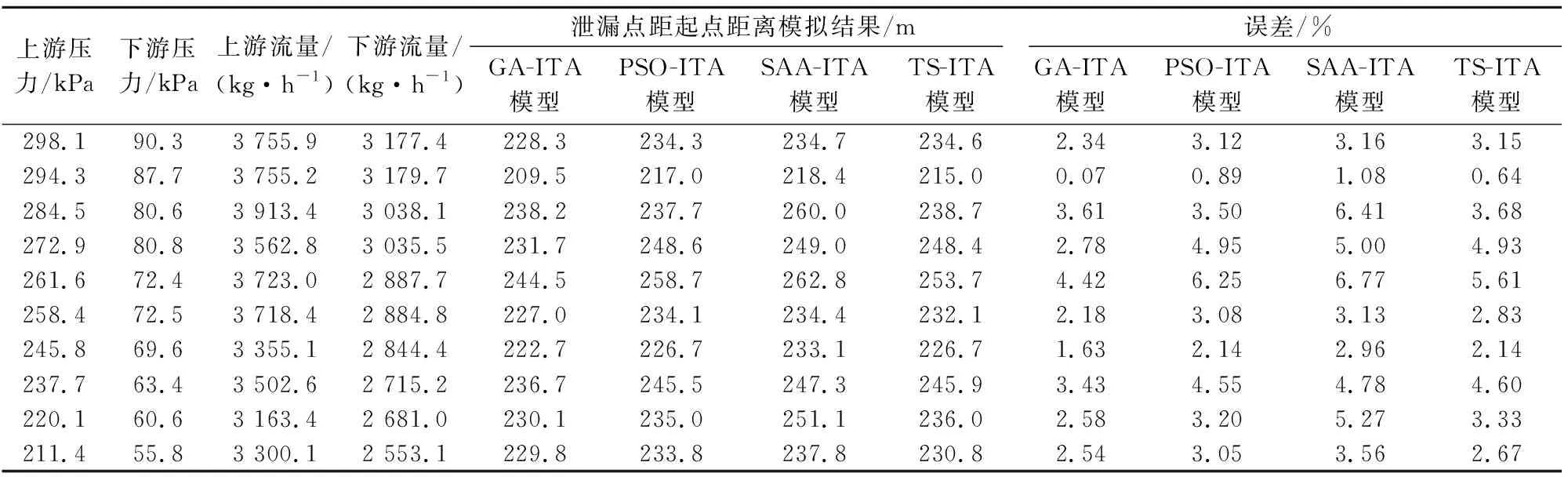
表2 泄漏点位于距起点210 m处时4种泄漏定位模型的定位结果对比

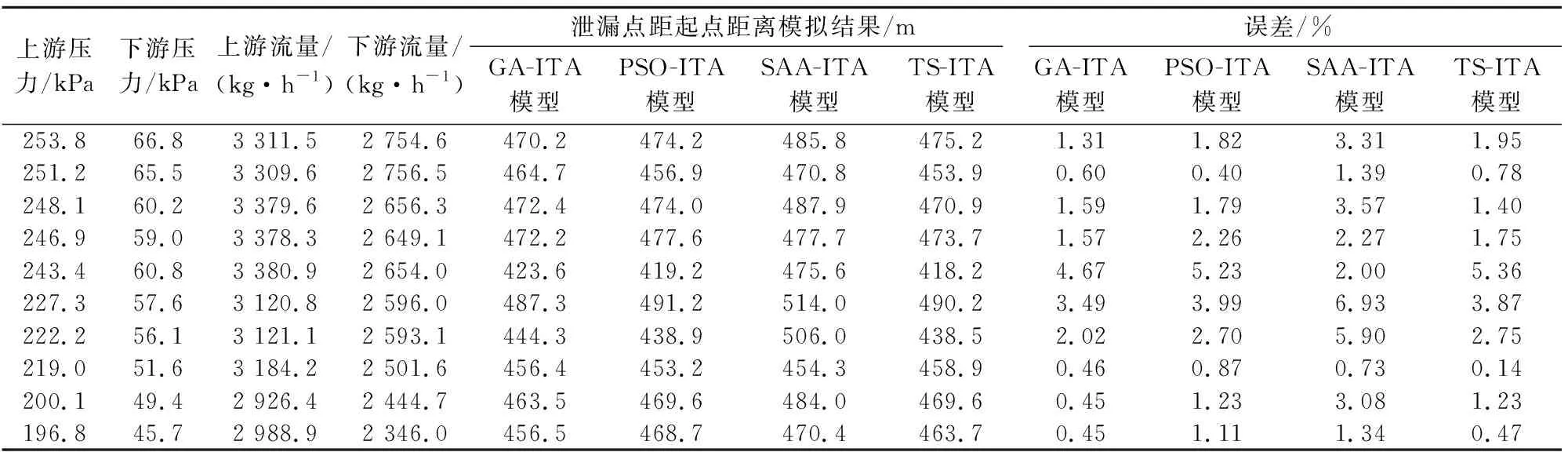
表3 泄漏点位于距起点460 m处时4种泄漏定位模型的定位结果对比

分析管道泄漏定位误差波动较大的原因主要有以下几点：

(1) 受噪声等因素的影响，仪表计量及数据传输存在误差。

(2) 室内试验设备安装有较多的阀门、三通等元件，其产生的局部阻力会造成当量管长和当量管道内径计算时存在误差。

(3) 该实验室建成至今已超过5 a，管道内壁存在生锈和结垢情况，管道内径及粗糙度发生了细微改变，这些都会影响试验的结果。

3 GA-ITA模型的适应性分析

考虑到室内试验管道规模较小、泄漏点位置固定、泄漏量变化范围有限，本文利用PNS管网仿真软件[23]分别建立了不同规模、不同位置和不同泄漏量的输油管道仿真模型，并基于仿真试验数据分析了GA-ITA模型的适应性。输油管道仿真模型的基本参数见表4。其中，仿真模型的管长变化范围为5～20 km；管道内径变化范围为100～400 mm；泄漏点位置分别设定在1/10、2/10、…、9/10里程处；仿真模型(1)和模型(2)的泄漏率分别设置为2%、5%和10%，仿真模型(3)和模型(4)的泄漏率分别设置为10%、15%和20%。

表4 输油管道仿真模型的基本参数

输油管道仿真模型的泄漏点定位结果见图7。

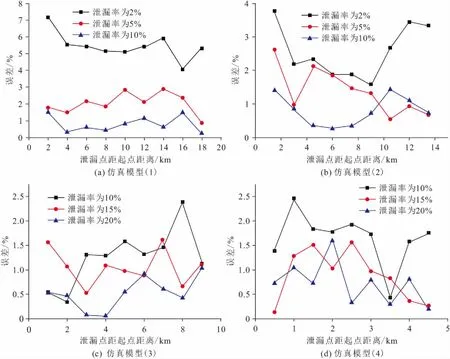
图7 输油管道仿真模型的泄漏点位置定位结果Fig.7 Leakage localization results of the oil pipeline simulation model

由图7可见，GA-ITA泄漏定位模型对于4种规模的输油管道，在不同泄漏工况下均能准确定位，仿真模型(1)至模型(4)的平均定位误差分别为2.8%、1.6%、0.9%和1.1%，说明该模型具有良好的适应性。

4 结论与建议

本文基于最优化理论建立了反瞬态分析(ITA)法输油管道泄漏定位模型，分别采用GA、PSO、SAA和TS 4种算法求解该模型，并结合室内试验数据对比了4种算法的计算速度和计算精度，同时结合仿真试验数据验证了GA-ITA模型的适应性，得到以下结论：

(1) GA、PSO、SAA和TS 4种算法均适用于求解ITA法管道泄漏定位模型，其中GA-ITA模型的计算速度最快(2.3 s/次)，管道泄漏定位误差最小(0.07%～4.67%)，因此遗传算(GA)法更适用于输油管道反瞬态分析泄漏定位问题的求解。

(2) 仿真试验结果表明：对于管长为5～20 km、内径为100～400 mm的管道，当泄漏率为2%～20%时，GA-ITA模型的定位精度较高，证明该模型适应性良好。

随着我国管道自动化与管网智慧化进程的加快，管道仿真技术与实时监控技术将进一步得到应用。反瞬态分析法充分利用实时监控数据，不需搭载额外的监控设备，在实际工程应用上具有极大的优势。但是，反瞬态分析法对实时数据质量与管道结构参数准确性的要求较高，数据噪声与管道模型参数的不准确性[24]对管道泄漏定位精度的影响较大。正如本文研究所示：当泄漏率为15%～23%时，基于室内试验数据的管道泄漏定位误差范围为0.07%～4.97%，基于仿真试验数据的管道泄漏定位误差为0.05%～1.6%。因此，该方法在实际应用时，应当结合数据降噪技术与管道参数自适应校正技术，以提高管道泄漏定位的精度。