面向云数据中心资源均衡分配需求的聚类调度算法研究

徐雨婷， 陈世平

（上海理工大学 光电信息与计算机工程学院，上海 200093）

由于全球经济的发展，云计算已经成为社会的一种重要计算模式[1]，并在发展过程中形成了性能佳、费用低、可靠性强等一些独特的特点。随着云计算数据中心数据量的快速增长，人们开始研究数据中心在进行资源分配的过程中如何提高系统资源利用率的方法[2-3]。

已有许多学者针对虚拟机−服务器的资源映射问题进行了研究。Selim 等[4]利用CPU 利用率差异概念，通过计算出所有物理服务器的CPU 利用率的最小方差，选择最合适的主机分配虚拟机，但该算法仅考虑了CPU 利用率，未考虑其他资源的使用情况。Combarro 等[5]针对三层数据中心提出了一种基于功率和网络感知调度模型，可通过资源整合和负载均衡调整的方式来实现降低能耗的目标，但未考虑资源利用率的优化。房丙午等[6]通过建立虚拟机放置模型，基于两个阶段的启发式算法来求解虚拟机放置模型，该启发式算法仅针对资源分配过程中的能耗问题进行研究，未考虑资源利用率的问题。

本文主要在包簇框架[7]基础上，研究数据中心资源调度策略。首先，基于包资源需求的分布密度，将资源需求（CPU 需求以及内存需求）具有差异性的包通过改进的k-means 算法进行聚类；其次，通过皮尔逊相关系数得到资源的相关性，定义包与簇之间的距离，将包映射到最近的簇；最后，通过Hadoop 框架和实验工具CloudSim 分别进行实验，验证包聚类算法以及资源调度算法的有效性。

1 传统的k-means 算法

传统的k-means 算法具有良好的可扩展性，kmeans 算法的思想主要是将聚类的中心点（质心）移动到聚类中包含其他样本点的平均位置，然后重新划分类。k值是通过算法计算出来的参数，表示类的数量。k-means 的参数包括类的质心位置及其内部观测值的位置。传统的k-means 算法过程如下[8]：

步骤1输入样本点集合，随机确定k个中心点；

步骤2计算样本集合中每个点到中心点之间的距离，将集合按照最小距离原则分配到最邻近聚类；

步骤3计算类中样本均值，更新每个类中心点的位置；

步骤4重复步骤2 和步骤3，直到所有中心不再更新或到达设定条件停止，输出k个类划分和最终的聚类中心。

2 包聚类算法

2.1 改进的k-means 算法初始值选定

为了解决传统的k-means 算法由于随机确定初始值对聚类结果造成影响的问题，需首先采用canopy 算法确定k-means 算法的初始值k及其初始中心[9]，通过canopy 算法对数据的预处理，可提高k-means 算法的处理速度，同时提高聚类准确性。

为了具体地实施包的聚类任务，采用基于canopy 算法的k-means 算法来实现包的聚类，将包的分布密度作为参数代入到canopy 算法中，并定义与包的CPU 需求、内存需求的相关距离度量因子，实现聚类过程。

将通过聚类形成的包简称为聚类包。现定义以下几种参数：

a. 集合中2 个需求差异最大的包之间的距离L。现假设集合中有点i:(xi,1,xi,2)，j:(xj,1,xj,2)，其中，xi,1和xj,1表示包的CPU 需求，xi,2和xj,2表示包的内存需求，若在某时刻这2 个包的需求差异最大，则将它们之间的距离定义为集合中包之间的最大距离。

b. 距离因子d(xi,xj)。d(xi,xj)表示聚类的距离度量因子，xi,xj分别代表包的CPU 需求和内存需求。

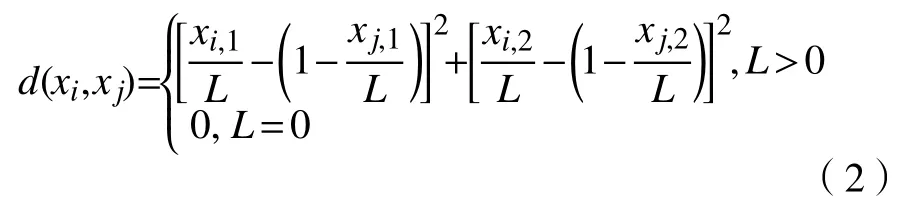
当L>0时，可由式（2）计算点i与点j之间的距离因子。以CPU 需求差异为例，若点i与点j的CPU 需求xi,1与xj,1之间的差异越大，则xi,1/L与(1−xj,1/L)的值越接近，则满足聚类原则中距离相近的点聚为一类的条件；当L=0时，表示集合中任意2 个包之间的资源需求均相等，包之间不存在资源需求差异，此时d(xi,xj)=0。因此，若包之间的CPU 需求、内存需求差异越大，则2 点之间的距离因子越近，最终需求差异大的2 个包将处于1 个聚类中。

c. 距离因子均值Dis。Dis为集合中所有包的距离因子的均值。n为集合中所有包样本点的数目。

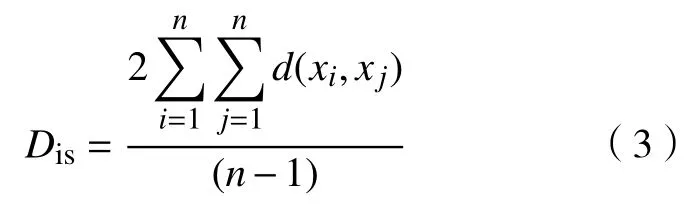
d. 包样本点分布密度f(i)。f(i)定义为集合中与包样本点i之间的距离因子小于Dis的包样本点数目，表示点i的分布密度，所有满足条件的包样本点构成一个聚类。

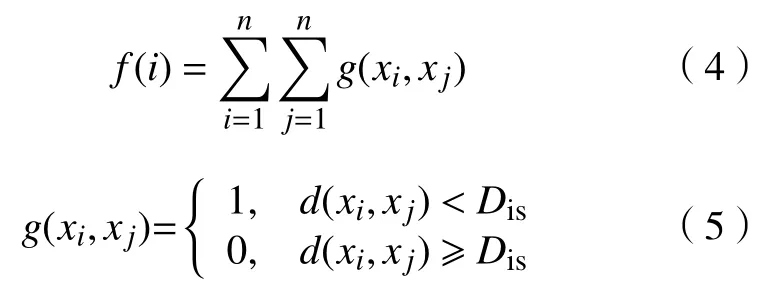
e. 聚类包中的距离因子均值 θ(i)。θ(i)表示已经形成的聚类包的距离因子的平均值。

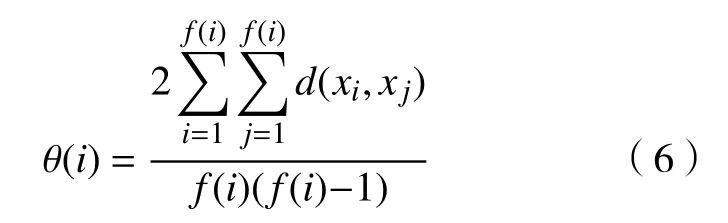
f. 2 个不同分布密度的聚类包的距离因子h(i)。h(i)表示聚类包中心点i与其他聚类包中心点之间的距离因子。现存在2 种情形：

（a）若存在聚类包中心点j1,j2,···,jR，R为聚类包的总个数，它们的分布密度均大于f(i)，分别计算点i与它们之间的距离因子，若点i与点jr(r∈R)之间的距离因子d(i,jr)最小，则h(i)=d(i,jr)。

（b）若点i的分布密度f(i)大于任意一个聚类中心点的分布密度，分别计算点i与其他聚类中心点之间的距离，若点i与点b之间的距离因子d(i,b)最大，则h(i)=d(i,b)。

g. 聚类包的最大分布密度乘积 µ 。由上述分析可知，f(i) 值越大，则i的周围的点就越多；θ(i)值越小，聚类包中的点就越紧密；h(i)值越大，则2 个聚类包的差异性就越大。由聚类的基本原则定义最大分布密度乘积µ, µ为聚类包中的距离因子均值、聚类包内的分布密度、聚类以后的包之间的距离的倒数这三者的乘积。

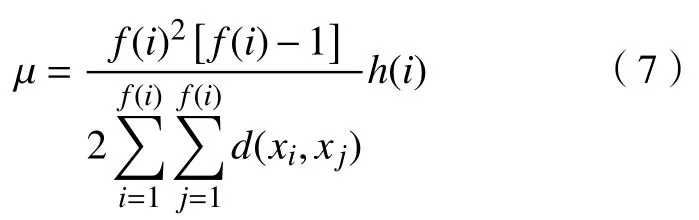
2.2 基于资源需求差异的k-means 算法

将基于资源需求差异的k-means 算法流程分为两部分进行描述，第一部分为基于canopy 算法确定k-means 算法的k值和中心，第二部分为k-means的算法流程。

首先介绍第一部分的算法流程。

步骤1定义由包组成的数据集D，计算集合中包的距离因子均值Dis和包样本点分布密度f(i)。

步骤2定义数据集A。步骤1 计算出的具有最大分布密度值的包a1被选择成为第一个聚类的中心点，将点a1加入到数据集A中，将满足与初始类中心点a1之间的距离因子小于Dis条件的所有包样本点从D中删除。

步骤3计算由步骤2 确定的D中剩余包样本点的 θ(i)，以及h(i)值，然后根据式（7）计算点i与a1之间的 µ 值，选择具有最大 µ 值所对应的点i，作为第二个聚类中心a2，并将a2放入集合A中。同样，将满足与a2之间距离因子小于Dis的包样本点从D中删除。

步骤4计算D中剩余的样本点i与a1和a2的之间的 µ 值，分别记作 µ1和µ2，选取具有最大分布密度乘积（µ1µ2）的点i，将点i作为第三个聚类的中心a3，并将a3放入集合A中。同样，将满足与a3之间距离因子小于Dis的包样本点从D中删除。

步骤5同理，若包样本点j与聚类中心a1，a2,…,ak−1之间具有最大分布密度乘积（µ1µ2···µk−1），则包j将被设置成第k个聚类中心。

步骤6循环步骤5，最终得到k值，以及初始类中心ai,i∈k。

由上述步骤最终确定的k值以及初始中心ai，代入到k-means 算法中，执行k-means 算法流程：

步骤1计算集合中每个包样本点i到ai的 距离因子。

步骤2将与ai之间的距离因子最小的样本点分配到ai所在的类中。

步骤3计算每个类中的平均值，并更新聚类中心。

步骤4重复执行步骤2 和步骤3，直到所有点聚类完成。

2.3 示例说明

假设在t时刻，有8 个待分配的包，如表1 所示。假设包需求为（1, 1）的含义是对CPU 的需求为1 核，对内存的需求为1 MB。

a. 定义集合D，并将表1 中所有包需求参数放入集合D中。首先根据式（2）分别计算8 个包的距离因子，根据式（3）计算出距离因子均值Dis，再根据式（4）计算包样本点分布密度f(i)。

b. 定义集合A，将分布密度f(i)最大的包设为第一个聚类中心点，首先选择f(i)最大为4 的包样本点，即编号为7 的包样本点，作为第一个聚类中心，将其放入集合A中，并将满足与编号为7 包样本点之间的距离因子小于Dis的样本点从D中删除，删除包编号为3，4，6，8 的样本点。

c. 通过b 的计算，D中剩下包编号为1，2，5 的点，再分别根据式（6）计算其 θ(i)，以及它们各自的h(i)，根据式（7）分别计算它们与b 确定的编号为7 的包样本点之间的 µ ，得出编号为1 的包样本点具有最大 µ ，作为第二个聚类中心，并将其放入集合A中，并将满足与编号为1 包样本点之间的距离因子小于Dis的样本点从D中删除，删除包编号为2，5 的样本点，此时集合D为空，基于分布密度的canopy 算法结束。

d. 执行k-means 算法聚类流程。根据上述步骤得到k值为2，初始类中心点为编号1 和7 的包。继续计算表1 中其他样本点与它们之间的距离因子，将距离因子与中心点最小的样本点分配到它们所在的类中，计算平均值，更新类中心，根据k-means 算法步骤，一直循环，直至聚类完成。

本示例形成了2 个聚类包。第一个聚类包括编号3，4，6，7，8 的包，其中，编号3，4，6 为对CPU 需求较高的包样本点，编号7，8 为对内存需求较高的包样本点；第二个聚类包包括编号为1，2，5 的包，其中，编号5 为对CPU 需求较高的包样本点，编号2 为对内存需求较高的包样本点。形成的2 个聚类包均为需求差异较大的包，由此可知，基于canopy 算法的k-means 算法可将资源需求差异较大的包聚类，从而提高各资源的利用率。最终得到的聚类结果如图1 所示。

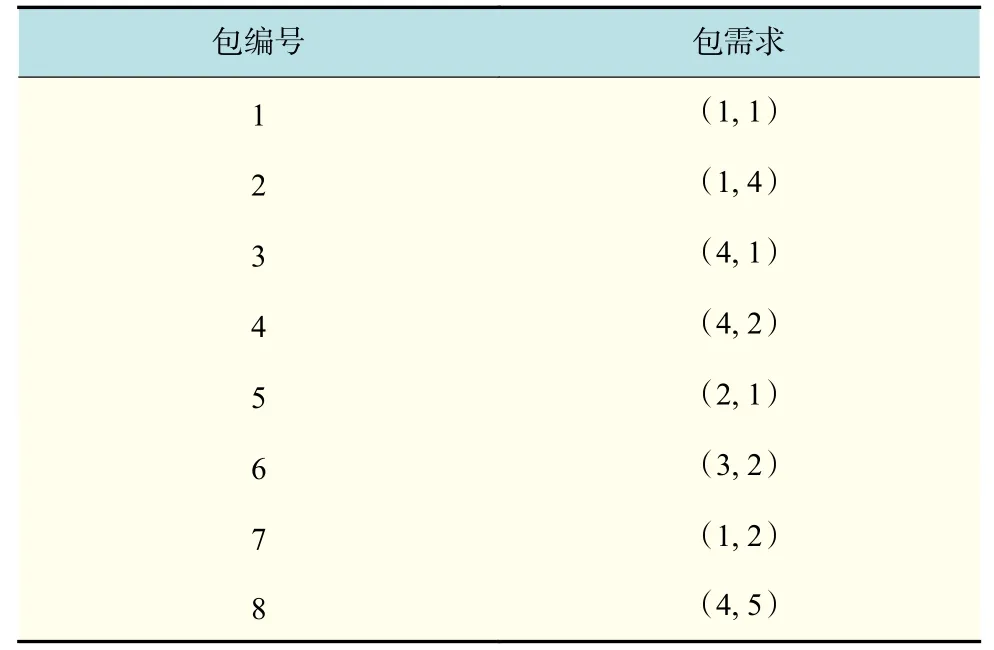
表 1 包需求参数（1）Tab.1 Package demand parameters（1）

图 1 聚类以后的包Fig. 1 Package after clustering

C1，C2 分别为第一个、第二个聚类包的聚类中心点。

3 包簇资源调度算法

3.1 包簇资源利用率及能耗定义

经过前面的聚类算法后，系统中共有k个待分配的聚类包，定义包集合为{x1,x2,···,xk}，定义簇集合为{y1,y2,···,yn}。现假设t时刻，包v(1 ⩽v⩽k)的资源需求总量为Rv[t]，簇p(1 ⩽p⩽n)可提供资源使用总量为Sp[t]，定义簇p中已使用资源总量为Wp[t]，规定每个簇的资源只能分配给一个包，即包中使用的资源不能超过簇中拥有的总资源，资源利用率

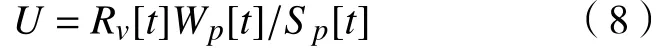
式中，0 ⩽U⩽1。

在资源分配过程中，除了需要考虑资源利用率以外，还需考虑资源分配过程中产生的能源消耗，可建立资源利用率与能耗之间的关系式[10]，式（9）为混合任务负载环境下的能耗模型。

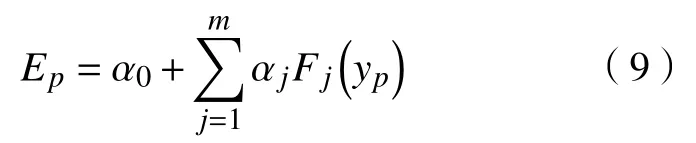
式中：Ep为能耗；Fjyp为Ep的核函数，由指数函数表示；yp为各类资源（CPU、内存）利用率； α0，αj为核函数的参数，由模型训练可得；m为用于训练的数据集中的数据总数目。

3.2 包簇之间的距离计算

簇与聚类包之间的距离由资源之间的相关性进行定义，采用Pearson（皮尔逊）[11]相关系数描述簇中已使用的资源总量与包的需求总量之间的相关性，分别将Rv[t]，Sp[t]，Wp[t]代入相关系数，由于相关系数ρRv(t),Wp(t)的因子取值为[0,1]，所以，将Rv[t]与Wp[t]进行归一化，再代入式（10），可得

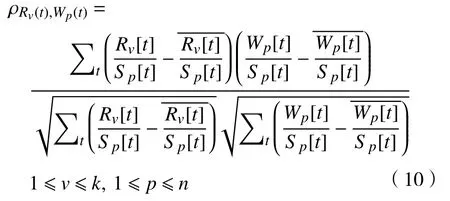
由于相关系数的区间为[−1,1]，因此，定义簇与聚类之后的包之间的距离

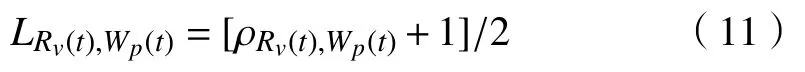
式（11）表示包簇之间的距离，区间为[0,1]，当由式（11）计算得出的LRv(t),Wp(t)值处于[0,1/2)时，表示Rv[t]与Wp[t]之间具有负相关性，具有负相关性的虚拟机与物理节点之间一般具有更多的资源互补[12-13]。因此，在进行包簇资源分配过程时，首先将包映射到与其距离的区间在[0,1/2)之间的簇，且在这区间中距离值越小，代表包与簇之间的资源互补性越大，最终可在资源分配时使得包能够集中映射到簇，从而减少簇的使用个数，提高资源利用率，降低分配过程中产生的能耗。

3.3 包簇资源调度算法的流程

基于改进的k-means 包簇资源调度算法（IKPC）步骤：

步骤1将所有待分配的聚类包放入队列，计算每个聚类的包到簇的距离，并将符合条件的聚类包映射到离它最近的簇中；

步骤2若簇资源不够分配给任何一个聚类包，则将聚类包放入队列尾部，直到聚类包找到具有符合条件的簇进行映射；

步骤3循环步骤1 和步骤2，直到所有的经过聚类以后的包映射到相应的簇中。

4 相关实验

实验1包聚类算法验证。

为了验证包聚类算法的有效性，现定义几种包参数，具体参数如表2 所示。包需求为（100，100）的含义是对CPU 的需求为100 核，对内存的需求为100 MB。

表 2 包需求参数（2）Tab.2 Package demand parameters（2）

通过Hadoop 框架的MapReduce 思想进行改进的k-means 算法的验算，实验结果如图2 所示。

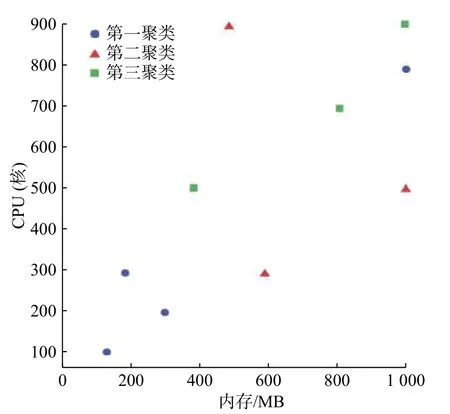
图 2 实验聚类结果Fig.2 Clustering experiment results

由图2 的实验结果可得，10 个包样本，经过聚类最终形成3 个聚类包。第一类包编号为1，2，5，8 的聚类包，编号2，8 为对CPU 需求较高的包，编号5 为对内存需求较高的包；第二类编号为3，4，9 的聚类包，编号3，9 为对CPU 需求较高的包，编号4 为对内存需求较高的包；第三类编号为6，7，10 的包，编号7，10 为对CPU 需求较高的包，编号6 为对内存需求较高的包。因此，本实验在将包进行聚类时，具有一定的有效性和灵活性。

实验2资源调度算法验证。

采用云仿真软件Cloudsim3.0[14]进行实验，实验环境中计算机参数为Intel Core i5-8250U CPU@1.60 GHz，内存为8.00 GB，64 位操作系统。

为了说明在资源调度算法之前首先将具有需求差异的包进行聚类的重要性，将本文的IKPC 算法与未经聚类直接采用资源调度算法（PC，package-cluster）进行对比，此外，进行对比的算法还有传统启发式算法、降序首次适应算法（FFD）[15]，FFD 算法是通常用来解决资源调度问题的方法。为了验证在包的需求更多以及簇资源规模更大时算法的有效性，现采用2 000 个簇和1 600 个包进行实验。

如图3 所示，本文中经过包聚类以后的IKPC算法的簇使用个数最少，相比未经过聚类，直接调用PC 算法的簇的个数少100 左右，相比于簇使用个数最多的FFD 算法，IKPC 的簇使用个数少500 左右。因此，本文中的IKPC 能在最少的簇中尽可能多地分配资源，具有一定的可用性。

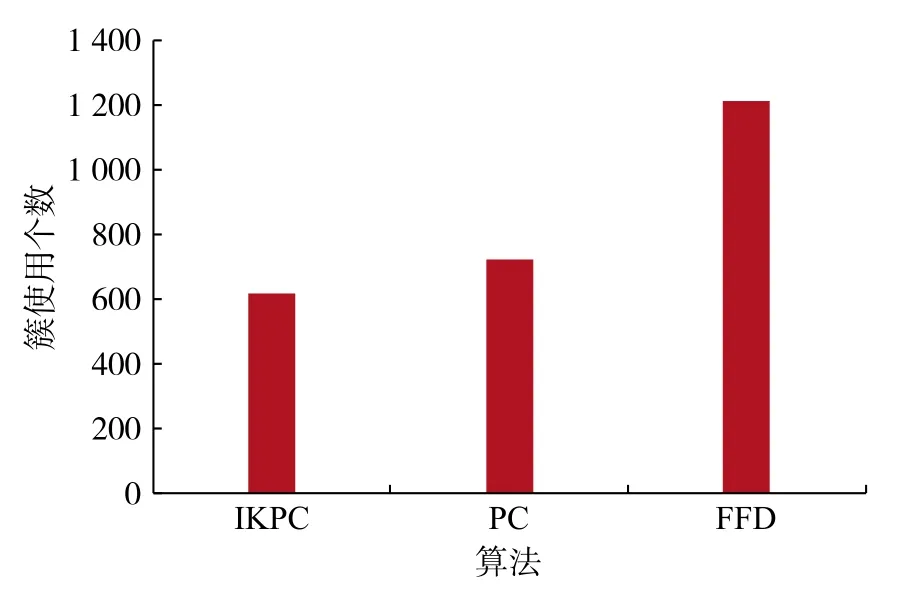
图 3 簇使用个数比较Fig.3 Cluster number comparison

如图4 所示，本文的资源调度算法IKPC 的CPU 利用率最高，FFD 算法与其他两种算法相比，其CPU 利用率最低。IKPC 算法比FFD 算法的CPU 利用率总体高10%左右，比未聚类的PC高6%左右。显而易见，本文的资源调度算法在CPU 利用率方面更有优势。

如图5 所示，IKPC 的内存利用率最高，相比于内存利用率最低的FFD 算法，IKPC 的内存利用率高了将近15%，比未聚类的PC 高7%左右。因此，本文的资源调度算法IKPC 在提高内存利用率方面具有有效性。

图6 为3 种算法的能耗比较结果。由于本文的IKPC 算法在资源分配过程中使得包能够集中映射到簇中，从而降低了资源分配过程中产生的能耗，而PC 和FFD 算法在资源分配过程中侧重于寻找合理的资源分配解，忽略了能耗、资源利用率的优化，因此，本文的IKPC 算法在降低数据中心的能耗方面具有一定的可用性。

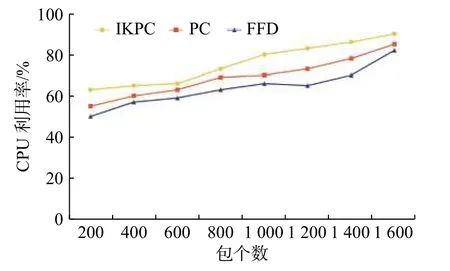
图 4 CPU 利用率比较Fig. 4 CPU utilization comparison

图 5 内存利用率比较Fig. 5 Memory utilization comparison

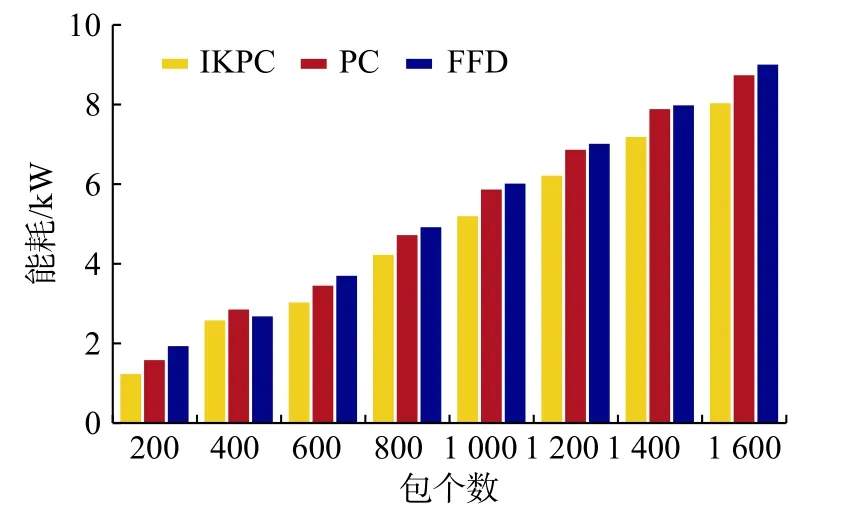
图 6 能耗比较Fig. 6 Energy consumption comparison

5 结束语

针对数据中心包簇框架下的资源分配问题，本文在进行包簇资源映射工作之前，首先将具有资源需求差异的包采用改进的k-means 进行聚类，然后，通过皮尔逊相关系数将聚类以后的包的需求和簇可提供资源之间的相关性作为距离度量因子，实现了包簇资源的映射。实验研究表明，改进后k-means 算法能够有效地对包聚类，资源调度算法能够有效地减少簇的使用个数，不仅能够提高各类资源利用率，而且可以降低数据中心由于资源分配而产生的能耗。