基于可靠度的高铁制动机周期预防维修优化研究
董航宇, 刘勤明, 叶春明, 刘文溢
(上海理工大学 管理学院,上海 200093)
1 问题的提出
高铁制动系统是能够使快速运行中的高铁强制减速或停止的装置。如果制动系统失效,不仅不利于列车的启动运行,而且还关系到运行中的列车能否安全停车,从而对旅客的安全造成巨大影响。本文对高铁制动装置的周期性预防性维修进行研究。
我国高铁发展速度快,维修理论也在不断地完善。长期以来,一直是采用定期维修、临时维修和事后维修的制度[1],具体框架如图1 所示。随着理论的深入,长期的维修也暴露出问题。第一,维修不足。制动机内部结构具有高度集成化、复杂化的特征,单纯依靠简单的机械磨损理论无法对故障规律进行精确的反映。第二,过度维修。出现过度维修是因为部件与部件之间存在性质上的差异,造成某些故障率低的部件存在过度维修的可能。设备在长期维修不足与过度维修的情况下工作,这使得设备的寿命不能发挥到最佳状态,设备的故障率高也直接影响着铁路系统的经济效益和可持续发展。

图 1 现阶段高铁维修模式Fig. 1 Current high-speed rail maintenance mode
卓明良等[2]基于无限时间域理论,研究了周期内时间成本函数与最优维护时间间隔之间存在的动态关系,在此基础上构建了以最低预防性维修成本为目标的函数模型。李荧等[3]提出了基于Monte-Carto 思想的统计模拟算法,利用故障信息计算预防性维修周期,对决策模型分布函数进行定义和参数估计,并根据实验结果验证了维修决策模型和算法的可靠性。郑睿等[4]提出了在时间延迟维修理论的基础上,利用发生故障数据和预防性维修后的初始数据的估计值来计算维修间隔期内故障次数的期望值,最终通过案例分析,计算出最佳的维修间隔期。Han 等[5]提出了在二维模式下预防性维修的模型,并对其过程进行分析,设计了二维预防性维修模型,通过实例分析了该模型的适用性和有效性。He 等[6]提出了面向可靠性的预防性维护,分析了制造阶段的产品可靠性的退化机制,并提出了3 种情景模型,分析每种发生的概率,最终通过一个案例研究验证所开发模型的性能。Kang 等[7]提出了一种综合控制模型,利用半马尔可夫决策过程的无限时间范围动态规划,以总生产成本最小化为目标,应用连续值迭代算法来获得近似最优控制策略,最后通过实例分析验证了该策略的有效性。
目前在铁路维修方面大多采用定期维修的方式,在顺序维修和多领域维修方面还需要进一步研究[8]。本文通过引入改善因子,基于可靠度的约束下,假设设备可靠度降低到某一阈值要进行一次预防性维修,以最低维修成本为目标函数,求得设备在寿命周期内的最佳预防性维修次数。结合当前研究的不足,分析了添加改善因子前后与成本的关系和可靠度与成本之间的关系。最后以算例结果证明了引入改善因子的有效性。同时该模型可用于设备实际的维修中,用来降低设备的总成本以及制定效率更高的维修计划。
2 研究方法
2.1 问题描述
设备性能随着寿命的增长而慢慢降低,从历史统计的故障数据来看,往往是故障率增加,役龄减小,即失效率随着时间的增大而增大,所以,在修复完后设备达到可靠度阈值所需要的时间也变得相对更短。本文假设设备的故障率服从Weibull 分布,Weibull 分布能够精确地描述设备的寿命问题,利用它可以大致推测出机电设备的剩余寿命、维修时间以及维修间隔,从而提高设备的使用寿命[9]。
2.2 模型假设
模型假设:
a. 设备的初始状态为全新状态。
b. 设备采用修复非新的政策,修补后不改变故障率函数。
c. 系统后备维修资源充足,发现故障可立即维修。
d. 假设车辆的保养工作放到夜间进行,不占用工作时间。
e. 设备在运行工作中的可靠度需高于最低可靠度阈值。
2.3 维修策略
当设备处于稳定运行的状态,随着里程的增加,可靠度降低到所设定需要进行维修的阈值时,在工作结束后即进行预防性维修。如图2所示,T1为维修周期,T2为预防维修时间。如果在还未达到正常需要预防性维修的时间发生了故障,则需要立即进行事后维修。有两种维修方式,即修补型维修和更换型维修。

图 2 预防性维修模式Fig.2 Preventive maintenance mode
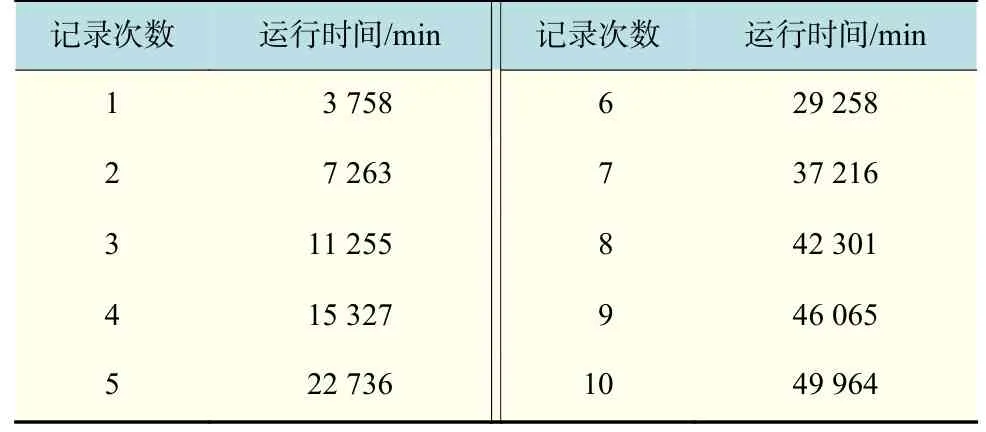
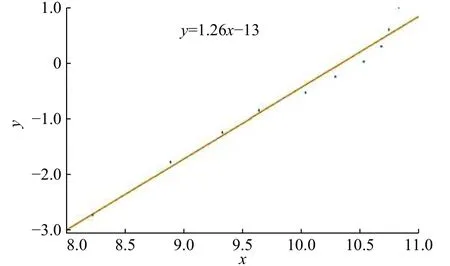
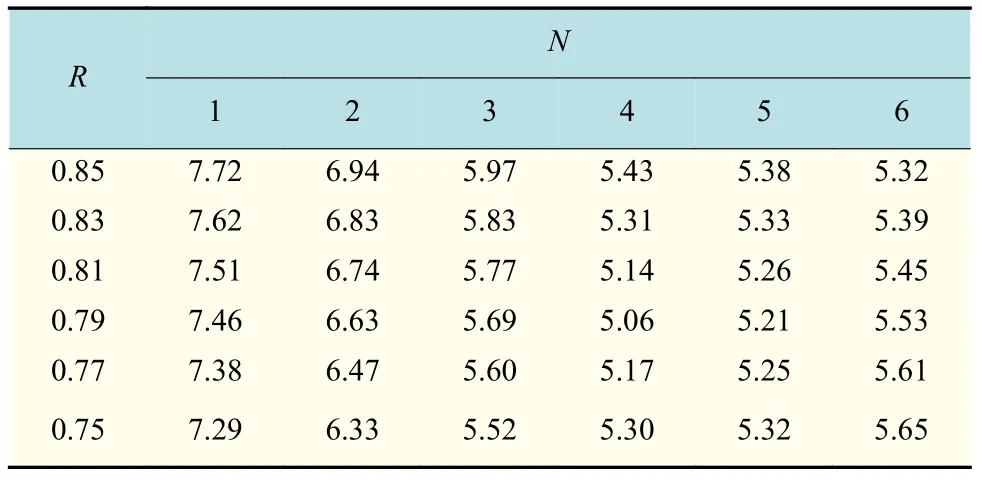
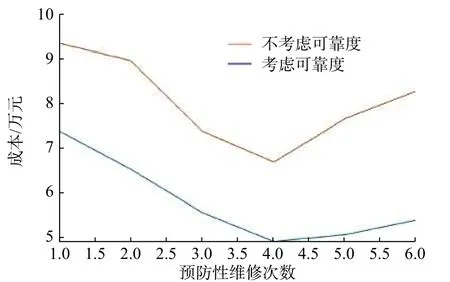
在图3 中,当设备正常工作到T1时需要预防性维修(T2)后继续工作,但下一个工作周期未达到正常工作周期(T1),仅到T3时(T3 图 3 修补性维修模式Fig.3 Patch repair mode 在图4 中,当预防性维修(T2)结束后继续工作到T3时(T3 图 4 更换性维修模式Fig.4 Replacement maintenance mode 高铁设备发生故障与多个因素有关,如系统、工作时间和环境。以高铁制动机为研究对象,在基于可靠度的预防性维修(preventive maintenance, PM)[10]的维修模式下,假设设备有一个可靠度的阈值,当设备的可靠度即将到达阈值R时,就进行一次预防性维修。可靠度表示为 式中:λij表示第i个维修周期内第j次预防性维修后的故障率函数;Rj为系统运行中的可靠度;Tij表示第i个维修周期内第j次和第(j+1)次预防性维修的时间间隔。 对式(1)取对数,可得 这说明在预防性维修周期内每次故障出现的概率相同。 由于设备的可靠度在实际运行过程中不是线性降低的走势,为了模拟设备真实的运行状态,使计算得到的数据更符合设备真实的衰减规律,有两种常用的改善因子[11−12]被广泛使用,即役龄递减因子ai和故障率递增因子bi。周晓军等[13]在文献[11−12]的基础上,同时考虑了两种改善因子的优点,建立了一种混合式的故障率演化模型。在预防性维修后设备的故障率函数为 式中:λi表示第i个维修周期的故障率函数;Ti表示第i次与第(i+1)次预防性维修的时间间隔;t表示运行时间的区间内的运行分钟数。 为了验证加入改善因子的作用,进行了对比分析。考虑改善因子情况下的故障率函数 式中:β为形状参数;η为尺度参数。 不考虑改善因子的情况下的故障率函数 设备在第i+1 个维修间隔期的失效率 对式(6)两边取对数,利用最小二乘法和微分学定理[13]可得役龄递减因子ai和故障率递增因子bi。 由假设可知,在设备的寿命周期中,设备在一个更换维修周期内的总费用式中:Cpk为一次预防性维修产生的费用;Cck为第k次故障产生的费用;Csk为第k次停机产生的费用;Crk为第k次更换产生的费用;Tik为第i个预防性维修周期内第k次与第(k+1)次的时间间隔;N为维修次数。 式(7)可简化为 设备的维修周期最低维修费用 式中:Tzk为总的运行时间;Rkm为设置的不同的可靠度;Nk为第k次运行的维修次数。 式(9)中Tzk可简化为 考虑可靠度时的最低维修费用 不考虑可靠度时的最低维修费用 从互联网中查找相关数据,得到高铁制动机发生故障的数据及对应的里程。现以我国最先进的复兴号为例,运行数据如表1 所示。 表 1 故障数据[14]Tab.1 Fault data 假设设备运行在50 000 min 内,因故障产生的费用Cc=10 000 元,单次预防性维修费用Cp为5 000 元,设备更换产生的费用Cr=15 000 万元,停机损失费用Cs=20 000 万元。计算中单次预防性维修时间T2=30,故障维修所需要的时间T3=60,更换性维修所需要的时间T5=90。假设改善因子设备初始役龄为0,初始可靠度R=0.9,R每降低0.05 需要进行一次预防性维修,系统可靠度Rmin=0.75。 Weibull 分布的失效率[15]引用式(6)。 故障密度函数 可靠度函数 故障率函数如式(4)所示。β,η通常从设备的历史故障数据中获得[16]。 利用最小二乘法进行参数估计,将式(6)两边取两次对数,可得 式中:F(Ni)为第i条数据第N次预防性维修后的失效概率,F(Ni)取累计分布函数的中位数;n为样本容量。 通过10 次故障所对应的里程数据拟合出一条直线,如图5 所示,得到方程y=1.26x−13。拟合求得B=β=1.26,A=−βlnη=−13,得到η=30 242。所以,尺度参数为30242,形状参数为1.26。设备故障率服从形状参数β=1.26、尺度参数η=30 242 的Weibull 分布。设备故障率函数 图 5 拟合数据Fig. 5 Fit data 由表2 可知,设备生命周期中最低维修成本Ck=5.06 万元,对应的可靠度阈值为0.79,最优预防性维修次数为4,即设备在第4 次预防性维修以后将进行更换。 若考虑可靠度的限制,可靠度最低值Rmin=0.79,模拟单位总成本随预防性维修次数N的变化趋势如图6 所示,最小单位成本为5.06 万元,对应的最佳维修次数N=4。若不考虑可靠度的限制,如图7 所示,最小单位总成本68 400,对应的最佳维修次数也为4。由此可以看出,若不考虑可靠度,设备会发生频繁的故障,成本将会增加,不利于设备长期的维修。 考虑改善因子时,设备的适用寿命相对不考虑改善因子时更长,在即将进行第6 次预防性维修时才会必须更换,如图8 所示,可靠度降低的程度也比较缓慢,对设备的充分利用有积极的作用。不考虑改善因子时,设备在第4 次预防性维修之后就达到了可靠度阈值,必须对该设备进行更换,过早地增加了设备更换的成本。 表 2 预防性维修次数、可靠度与成本之间的关系Tab.2 Relationships between the times of preventive maintenance, reliability and cost 万元 图 6 R=0.79 时预防性维修次数与成本的关系Fig. 6 Relationship between the times of preventive maintenance and cost when R=0.79 图 7 考虑可靠度与不考虑可靠度时预防性维修次数与成本的关系Fig. 7 Relationship between the times of preventive maintenance and cost when considering or not considering reliability 根据以上分析可知,无论在考虑或不考虑可靠度时,设备最佳维修次数都为4 次,但是,不考虑可靠度的情况下,小修次数将会增多,导致设备停机次数增加,成本将会增加,不利于设备的正常运行。当不考虑改善因子时,设备可靠度降低的斜率会相较于考虑改善因子时大,导致设备需要更早地更换,同样,成本也会增加。 图 8 考虑或不考虑改善因子时预防性维修次数与可靠度之间的关系Fig. 8 Relationship between the times of preventive maintenance and reliability when considering or not considering improvement factors 通过对高铁制动机周期性预防维修的研究,建立了基于可靠度约束下的最低维修成本策略模型,并通过引入了改善因子,描述设备的正常衰退情况。算例还考虑了添加与未添加改善因子情况下分析比较可靠度下降的趋势,以及考虑与不考虑可靠度限制时两种情况下与成本之间的关系。结果表明,在加入可靠度与改善因子之后,设备运行时间50 000 min 内维修次数由10 次降低为4 次,同时停机次数减少,设备生命周期内成本相较于未加入前有明显的降低,本文改进后的算法对现实生活中设备的维修有一定的参考价值。但是,本文算例得出的故障率递增因子与役龄递减因子的数学表达式的计算有过于理想化的情况,未来可以从故障记录中发掘因子与周期数和维修序数的耦合度来进行全面的研究。

3模型建立
3.1 可靠度
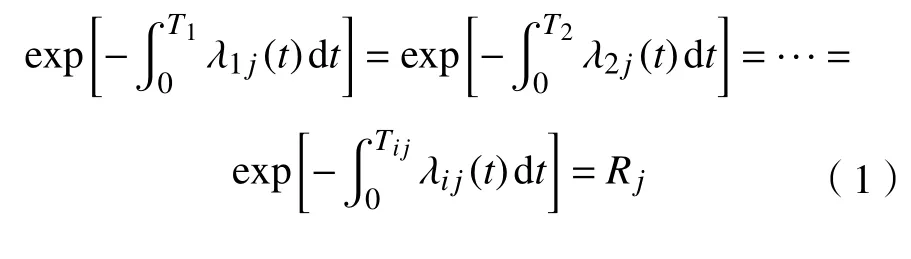
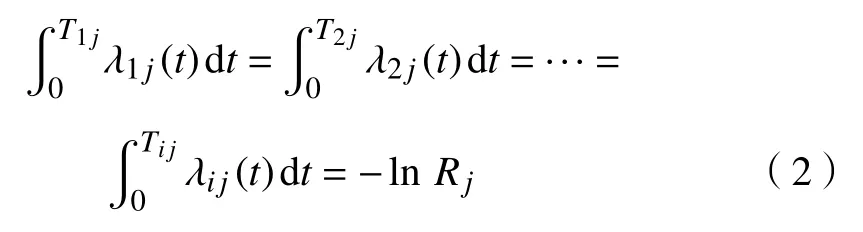
3.2 改善因子
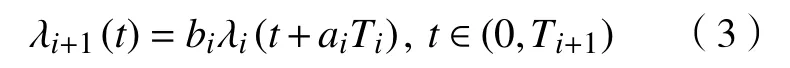
3.3 故障率函数
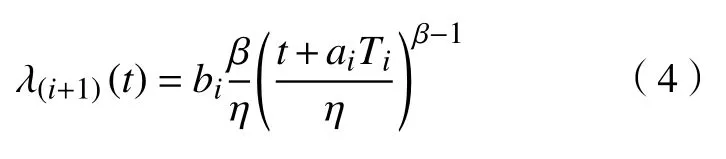

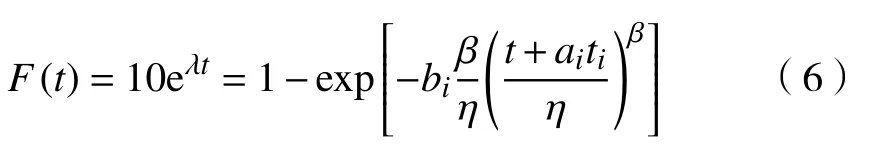
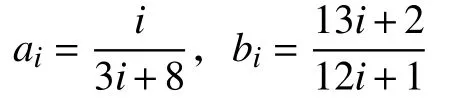
3.4 数学模型
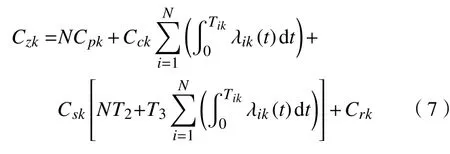

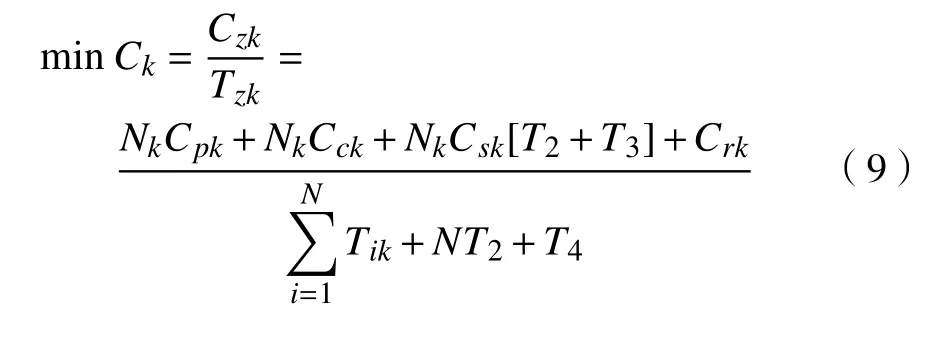
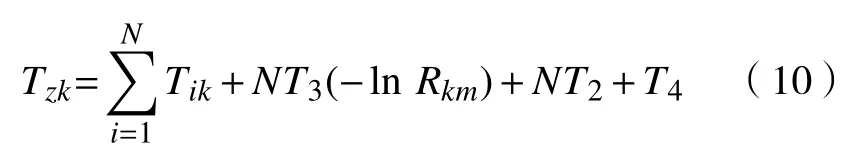
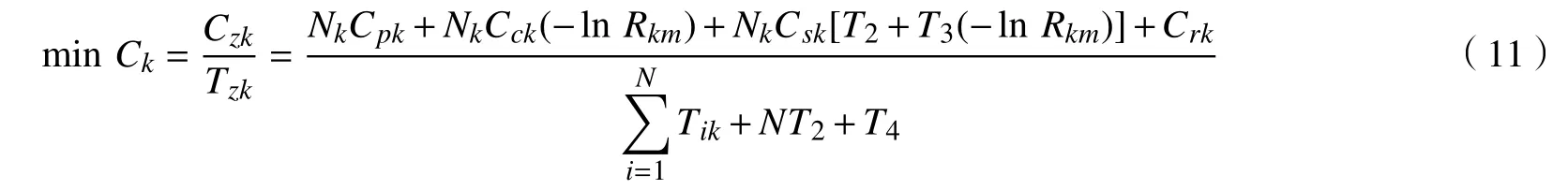

4 算例分析
4.1 设备故障率分析

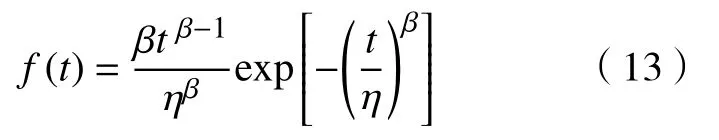
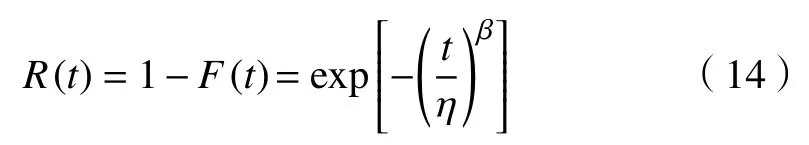
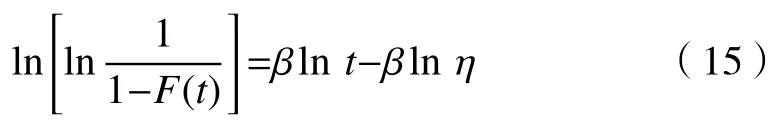

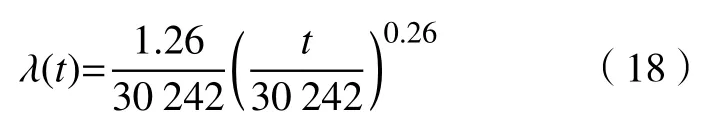
4.2 结果分析


5 结 论

