设备故障过程的建模与仿真研究
郑 睿
(上海财经大学 公共经济与管理学院,上海 200433)
我国企业对设备管理主要是采用计划预修制,其核心工作之一是确定出合理预防维修(preventive maintenance,PM)计划,以便达到减少设备停机时间的目的[1]。实践中我国企业主要凭维修工程师的经验或根据厂家规定的说明书来制定维修计划,一直存在维修不足和维修过剩两大问题[2]。
考虑到我国大中型企业都有比较完整的故障记录数据,包括:每次故障发生时间及其修理时间、每次PM 活动所需要的时间及其检查发现的缺陷个数。因此,借鉴时间延迟维修理论[3-5]。在分析和应用这些记录数据的基础上,通过建立故障过程模型,揭示故障机理。同时为了证实故障过程模型的正确性,建立设备故障过程的计算机仿真系统。
目前有关故障过程仿真的研究主要集中于以下几个方面:a. 从材料的物理性能角度,分析各种材料性能失效过程,提示各种材料的失效机理[6-7];b. 基于机器学习的仿真方法,诊断复杂设备系统的故障部位,分析故障形成的原因,从而解决实故障部位难以发现的实际工程问题[8];c. 应用仿真方法,联合决策生产计划和预防维修计划[9],或应用蒙特卡罗仿真方法[10],模拟故障过程并进行维修决策。这些研究从不同角度揭示设备故障,或材料失效的过程。但是从数学建模角度,建立故障过程模型和仿真系统,这方面工作有待深入研究。
故障过程模型与仿真系统的建立,将有效解决我国多年来存在的定期维修计划科学性不足的难题,对于提高设备利用率,降低维修费用具有重要理论意义和实践价值。
1 问题描述
设备劣化是一个随机过程。具体劣化过程又分为两个阶段,首先是缺陷的发生,然后缺陷进一步劣化成为故障。从缺陷发生到故障发生的时间间隔称为时间延迟[3],记为h。缺陷发生是随机的,时间延迟也是随机的,这就是为什么维修决策难的原因。
正如前言指出:计划预修制核心工作之一是如何制定出合理PM 计划,或者PM 周期。国际上比较好的做法是,利用故障记录数据(每次故障发生时间和停机时间)和PM 检查数据(PM 活动时检查出的缺陷次数),得到设备的缺陷发生率λ、时间延迟h的分布函数。在参数估计的基础上,计算出维修间隔期T内故障次数期望值,以及PM检查出缺陷次数的期望值。最终应用检查模型计算出最佳PM 周期[11-13],如图1 所示。图中:Ti为第i次PM 活动的时间(i=1,2,···,m);t(i−1)j为(Ti−1,Ti)期间第j次故障时间,其中j=1, 2, ···,ki−1。

图 1 在(Ti-1,Ti)期间各次故障发生时间及PM 活动观察到的缺陷次数Fig.1 Observed failures and number of defects over time(Ti-1,Ti)
问题在于:a. 建立的故障模型是否正确,如何验证?只有故障模型验证正确之后才能应用来进行维修决策;b. 当缺乏故障记录数据时,如何对故障模型进行参数估计?解决这些问题的对策:建立故障过程仿真系统,仿真系统生产的故障记录数据和检查数据,作为故障模型参数估计的原始数据;应用这些仿真数据估计出模型参数,如果与输入数据一致或在误差范围之内,则证实所建立故障模型的正确性,从而可以应用故障模型制定维修计划。
2 完全检查下设备故障模型的建立
2.1 假定条件及有关符号
通过对设备故障记录数据的分析,本文提出了以下假定条件:
a. 检查是完全的,PM 活动能检查出所有存在的缺陷;以及所有检查出的缺陷在较短时间内得到修复;
b. 缺陷的发生率为齐次泊松过程(HPP,homogeneous Poisson process);
c. 各个缺陷的发生是相互独立的,以及缺陷发生和故障发生也是两个独立的事件。
相应地,符号记为:λ为缺陷发生率;v(t)为故障发生率;h为时间延迟,其分布函数和概率密度函数分别记为F(h)和f(h);ENf(Ti−1,Ti)为(Ti−1,Ti)期间故障次数的均值;ENp(Ti)为在Ti时检查发现的缺陷个数的均值。
2.2 最大似然函数
在(Ti−1,Ti)期间所有的事件,包括:在Ti时观察到缺陷数ni,各次故障发生时间(见图1),i=1, 2, ···,m。似然函数即是所有这些观察事件概率的乘积,用L表示。

对式(1)两边取对数,得

a.p(在t(i−1)j发生故障)的计算。
如果缺陷的发生服从HPP,发生率为λ, 由u时发生缺陷所引发的在t时的故障发生率v(t)为

式中,Ti-1 相应地,在(t(i−1)j,t(i−1)j+Δt)区间发生一个故障的概率为 b.p(在(Ti−1,Ti)期间各记录故障之间无故障再发生)的计算。 由于故障过程为NHPP, 得到: 在(Ti-1,Ti)期间故障之间无故障再发生概率的对数函数为 c.P(在Ti时检查出ni个缺陷)。 在Ti时刻检查出缺陷个数的均值ENp(Ti)为 缺陷发生率为泊松过程,以及Ti时刻检查出缺陷个数的均值为ENp(Ti)。因此,Ti时刻PM 活动检查发现ni个缺陷的概率为 式(4)除以Δt,对式(8)取对数,则对数似然函数表示为 根据故障记录数据和PM 检查数据,包括各个故障发生时间,以及PM 活动时检查出的缺陷个数,求式(9)最大值,即估计出参数λ和f(h)。 设备缺陷发生以及缺陷劣化成为故障,整个故障过程的仿真流程见图2。图中:RND()表示随机数;Int()表示对ti取整数;Nd(k)表示在KT同期内的缺陷数;Nf(k)表示在KT周期内的故障数。为了简单起见,假定时间延迟分布函数为指数分布,并最初设定λ=1.33,α=0.28,维修间隔期为7 d。具体步骤如下所示。 Step 1 产生缺陷的过程(服从泊松分布)。 其算法如下所示: 若计数过程{Nt,t≥0}是一个具有到达率为λ的齐次泊松过程,则它相应的到达时间间隔A1,A2,···是一个具有参数1/λ的独立分布的指数随机变量。 图 2 完全检查下设备故障过程的计算机模拟仿真流程Fig. 2 Flowchart of simulation of the failure process of the equipment in case of perfect inspection 根据这一定理,如果泊松过程的到达时间为u1,u2,···,则到达时间间隔Ai=ui−ui−1(i=1, 2, ···)是一个指数随机变量(参数1/λ)。因此,可循环地产生ui(假定ui−1已经确定,且u0=0) a. 产生U~U(0,1); b. 置ui=ui−1−(1/λ)lnU; Step 2 计算每一个缺陷的时间延迟函数。 由于F(x)=1−exp(α,x),记每一个缺陷的时间延迟为h1,h2,···(i=1, 2, ···)。因此,可循环地产生hi: a. 产生U~U(0,1); b. 置hi=−(1/α)lnU。 Step 3 统计每一周期中缺陷的个数和故障的次数。 计算t(i)=u(i)+h(i)。a. 如果t(i) 按照上述步骤,仿真10 次,共产生样本数91 个,各个维修间隔期内发生的故障次数及PM活动时检查出的缺陷个数见表1。 将上述模拟仿真产生数据(故障发生时间、PM 检查发现的缺陷个数)代入式(9)中,进行参数估计,得=1.3000,=0.2798。仿真结果表明所建立的故障模型是正确的。 一旦证实故障模型正确后,即可应用检查模型制定出PM 计划,具体应用案例可参见文献[1, 5]。 表 1 各个周期内发生的故障次数及PM 检查时发现的缺陷个数Tab.1 Number of failures in different cycles and defects identified in PMs 研究表明:a. 所建立的故障过程模型和故障过程仿真系统,直观显示从缺陷发生到故障形成的过程,特别是故障过程仿真系统的建立,解决了故障记录数据缺乏下验证故障模型正确性的难题;b. 输入故障记录数据,如每次故障发生时间,以及每次PM 活动检查发现的缺陷个数,应用所建立的故障过程模型,即可估计出缺陷发生率和时间延迟分布函数等参数。一旦得出这些参数,即可应用检查模型制定出科学的PM 计划,从而有望有效解决多年存在的维修不足和维修过剩两大问题。



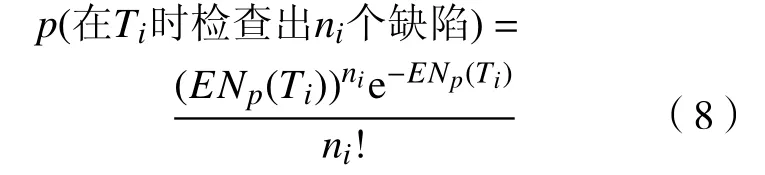
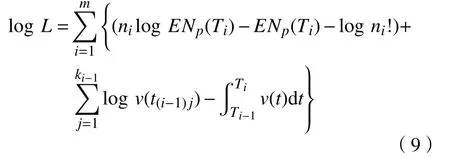
3 故障过程的仿真与结果分析


4 结 论

