铜箔一体机张力的模型预测控制

王 同，夏 春

（安徽铜冠铜箔有限公司，安徽池州 247100）

0 引言

随着5G时代的来临，市场对高端电子铜箔的需求日益增加，提高6μm及以下等超薄电子铜箔的产量和质量是铜箔企业在当今时代面临的机遇和挑战。张力是影响电子铜箔产量和质量的关键因素之一[1]。张力过大导致电子铜箔紧绷，难以抵御非水平辊产生的径向剪切力，容易发生撕边现象；张力过小导致箔面松弛，容易受到机械抖动影响而发生起褶现象。张力控制分为恒张力控制和变张力控制[2]，收放卷张力控制受到卷径变化影响都是变张力控制。因此，需要合适的张力控制方法同时具备稳态波动小和动态响应好的特点。

现有的生箔一体机设备有很大一部分来自于国外进口，难以进行结构和功能上的改造，如何在维持现有结构的基础上选择合适的控制方法达到预期的张力控制效果是一个值得研究的问题。由于生箔机张力模型描述的是具有复杂非线性强耦合时变特点的系统[2]，因此相应的控制方法必须具备较强的鲁棒性和扰动抑制能力。常见的张力控制方法包括PID、神经网络[3]、模糊控制[2-4]和模型预测控制[1]等。其中神经网络和模糊控制实现复杂，难以移植到现有的结构上。传统的PID方法结构简单、实现容易，但是由于铜箔弹性模量大、外环控制周期长、控制器性能受限，导致动态响应速度慢且超调大。而模型预测控制不受外环控制周期限制，且具有响应速度快、超调小的特点，因此选择设计基于模型预测控制的控制器。

1 铜箔一体机张力模型建立

张力是由于弹性物体发生弹性形变而产生的。由于铜箔的弹性模量较大，根据凯尔文-沃伊特模型，可以忽略微分项。简化后的铜箔张力表达式为：

T=εEA（1）式中：ε为单位长度物体拉伸部分的形变量；A为物体的横截面积；E为材料的弹性模量；T为铜箔张力。

铜箔一体机系统结构如图1所示。该系统呈现出多输入多输出的特性。电机1由变频器单独控制，用于设置机列线速度参考。通过控制电机2和电机3的转速可以分别控制剥离和收卷张力。对应于剥离、加工处理和收卷的不同功能需求，将系统张力分为Ⅰ段、Ⅲ段和Ⅱ段。因此，整个系统的张力模型分为3段，首先对剥离段（Ⅰ段）张力建模，如图2所示[2-3,5-9]。

图1 生箔机系统结构示意图

根据物体拉伸前后质量守恒，可以得到关于拉伸前后横截面积A和拉伸长度dx的表达式：

式中： ρ为物体的密度；n为处于未拉伸状态。由于：

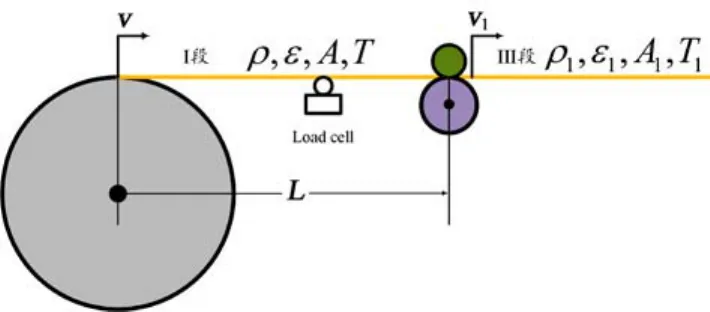
图2 剥离段张力模型

所以，根据式（2）～（3）可以得到拉伸后横截面积和拉伸前横截面积及形变量的关系：

根据质量守恒定律，Ⅰ段的质量变化量等于单位时间内进入该段的质量减去离开该段的质量，即：

式中：i为进入；o为离开；L为Ⅰ段的长度；v为铜箔的线速度；A为Ⅰ段的横截面积；Ai为进入Ⅰ段前的横截面积；Ao为离开Ⅰ段后的横截面积。根据拉伸前后铜箔密度不变，得到ρ=ρi=ρo，将式(4)代入式(5)并作相应变换得到：

为了和Ⅱ段、Ⅲ段加以区分，令V为进入Ⅰ段的铜箔线速度，也即钛辊的线速度；V1为离开Ⅰ段的铜箔线速度，由电机2控制。铜箔从钛辊上析出后进入Ⅰ段，由于铜箔均匀析出，可以认为进入Ⅰ段前铜箔拉伸形变量ε0=0。因为

式中：T为Ⅰ段的张力。至此，得到Ⅰ段的张力模型。同理可以得到Ⅱ段，即收卷段的张力模型为：

式中：V1为进入Ⅱ段的线速度；V2为离开Ⅱ段的线速度，也即收卷辊的线速度。

III段的张力模型为：

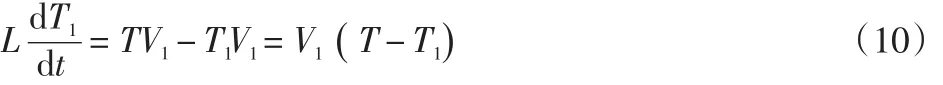
式中表明稳态时，III段的张力和Ⅰ段的张力相等，原因在于两个压辊由同一个电机控制，线速度相等。

收卷段张力模型如图3所示。

系统的连续状态空间方程为：

其中，状态变量为：

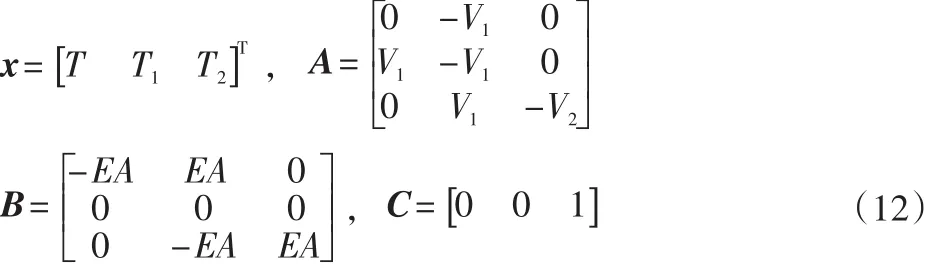
图3 收卷段张力模型

2 模型预测控制

模型预测控制把控制问题转化为数学优化问题，根据评价函数选择激励动作。模型预测控制的思路是采样当前时刻的系统状态，根据系统模型，预测未来一段时间内的输入增量引起的系统状态变化，将预测得到的未来系统状态代入到评价函数中，选择评价最高的输入增量作为当前时刻的激励。预测的时间步数为NP，施加控制的时间步数为Nc，超出预测步数的控制没有意义，因此，Np≥Nc。根据预测时间步数是否为1，可以分为单步预测和多步预测。单步预测仅考虑下一个时刻的系统状态，多步预测考虑未来多个时刻系统状态的综合评价，因此，多步预测在动态响应和稳定性上通常优于单步预测。这里采用多步预测的方法，并且使用滚动时域控制，每次仅采用增量控制序列的第一个，可以提高控制器的鲁棒性和抗扰动能力。

为了得到增量控制序列，将离散后的状态空间模型表示为增强模型[9]。其中，Δu(k)=u(k)-u(k-1)为输入的

式中：y( ki+N| ki)T为基于当前ki时刻、N(N∈{1 , …,Np})时刻后期望输出的列向量。增量控制序列为：

评价函数选择为预测时间步数内期望输出和实际输出的误差平方和，如下式所示：

由于评价函数是一个凸函数，因此可以用解析的方法得到全局最小值，使得评价函数最小的解如下式所示：

根据滚动时域控制，对于整个输入增量序列，仅仅取第一个作为下一时刻的控制输入增量。

3 仿真验证

为了观察对比PID控制和模型预测控制的效果，在Matlab中，分别搭建了用PID和用模型预测控制的仿真实验平台。控制框图如图4所示。

图4 控制框图

根据实际生产的情况，假设钛辊的线速度为机列参考线速度，且钛辊的线速度V由变频器单独控制成S曲线。仿真参数如表1所示。

表1 仿真参数设置

仿真从t=0时刻，钛辊速度从V=0开始按照S曲线上升，给定放卷张力为Tref=400 N，收卷张力为T2ref=600 N。系统的动态响应对比如图5所示，可以看到模型预测控制比PID控制有更快的动态响应速度，并且超调更小。

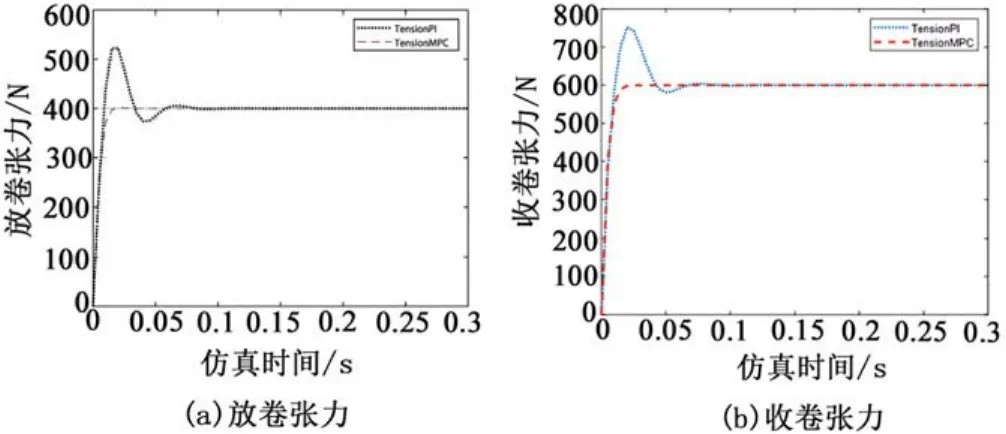
图5 PID和模型预测控制控制效果对比

4 结束语

本文介绍了铜箔一体机的张力模型，该模型能较为精确地描述系统行为，并且具有较好的控制效果。张力外环的时间常数较大，且铜箔的弹性模量较大，传统PID控制动态响应较慢且超调较大。采用模型预测控制，在低频的情况下能保证计算时间，同时比传统PID控制有更好的动态响应。在生箔机等对张力控制性能要求较高的领域可以使用模型预测控制。