基于流固耦合的油底壳振动噪声预测分析

宋兆哲 李荣荣 高锋军 杨景玲

(长城汽车股份有限公司 河北省汽车工程技术研究中心 保定 071000)

0 引言

发动机上的罩壳类零部件(如油底壳、正时罩、缸盖罩等)，由于其具有面积大和壁薄等特点，且覆盖在发动机外表面，常常成为发动机的主要辐射噪声源[1-2]。同时，油底壳几乎完全裸露于汽车的底部且辐射面积大，显得尤为严重，一些研究资料显示，油底壳产生的辐射噪声约占总噪声的24%，是最大的表面辐射噪声源[3-4]，因此，开展油底壳振动噪声预测分析很有必要。

由于油底壳在工作过程中含有至少3/4以上的机油，且机油的密度比较大，工作时油底壳受到来自发动机的激励而振动，该振动能量会传递给与其接触的机油上，使机油振动从而产生声压，该声压会进一步传递到与机油接触的油底壳上，对油底壳的振动噪声产生影响，所以，油底壳的振动噪声是机油和壳体耦合作用的结果，忽略他们之间的耦合作用，计算结果与实际结果难以对应[5]。

忽略耦合模态计算的边界条件，缩小模态计算和测试结果误差，但噪声实际测试误差增大无法解释[6-9]。为了研究约束条件和油量对油底壳辐射噪声的影响，以某1.5 T 发动机油底壳为研究对象，建立油底壳的耦合有限元模型进行耦合模态计算，获得其固有频率和振型，通过油底壳安装在发动机上的模态试验验证了耦合有限元模型的误差范围。将实际发动机工作过程中测得油底壳各螺栓固定处的振动加速度，进行格式转换处理后加载到模型上；即在模态验证后的油底壳模型螺栓固定处施加实测的振动加速度，采用有限元流固耦合的仿真分析方法，对油底壳进行强迫振动计算和辐射噪声计算，并与试验对比。然后对含油量多少对辐射噪声的影响进行对比分析。该振动噪声的预测分析方法，用于发动机开发试验确认阶段，对油底壳改进优化方案进行振动噪声的预测，减小开发NVH大风险。

1 耦合声学有限元法

1.1 耦合问题的简单判定

进行耦合问题的判定时，可采用耦合系数λ来对耦合作用的强弱进行简单判定：

其中，ρf为流体密度，即本文中的机油密度；c为声音在该流体中的传播速度；ρs为固体密度，即本文中的油底壳密度；T为固体等效厚度，即本文中的油底壳壁厚；ω为角频率。

当λ＞1 时，判定为强耦合，需考虑耦合作用；当λ ≪1 时，判定为弱耦合，可不考虑耦合作用，但是对一些特殊领域，需要结合实际情况对待[5]。本文中使用的参数如表1所示，经计算，耦合系数λ=17.8，认为机油和油底壳之间是强耦合的，必须进行耦合计算。

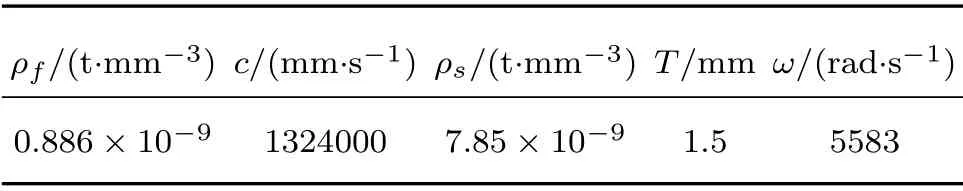
表1 参数Table 1 Parameters

1.2 耦合声学有限元法介绍

常用计算耦合问题的方法有耦合声学有限元法和耦合声学边界元法，本文采用前者计算。因为计算耦合问题时，需要在同一个耦合环境里面同时对结构振动和声场分布进行计算，所以，在计算耦合问题时，需要考虑结构动力方程、流体运动方程与连续性方程直接的相互影响，其声学波动方程为

其中，Mf为声学等效质量矩阵；Cf为流体等效阻尼矩阵；Kf为声学等效刚度矩阵；R为结构与流体的耦合矩阵；p为网格节点声压矩阵；为单元节点位移的二阶导数矩阵。

在不考虑声压对结构的振动影响时，其结构动力方程为

其中，Ms为结构质量矩阵；Cs为结构阻尼矩阵；Ks为结构刚度矩阵；u为结构位移矢量矩阵；Fs为结构外激励矩阵。

流固耦合计算时，不仅要考虑结构的外激励，而且还需考虑声压对结构振动影响，所以需要在结构与流体的接触面上加上流体产生的压力载荷，此时对应的结构动力方程为

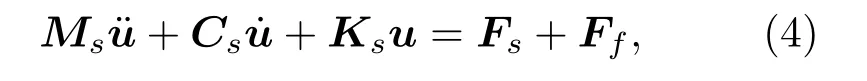
其中，Ff为耦合界面上流体压力载荷矩阵。

综合式(2)和式(4)得到流固耦合方程为[6-7]

2 油底壳流固耦合模态分析及校对

2.1 耦合有限元建模

本文采用的油底壳为冲压钢板结构，厚度为1.5 mm，机油含量约占据整个油底壳。首先，用Creo软件建立油底壳的结构和机油几何模型；其次，将以上几何模型导入到前处理软件中，对油底壳抽取中面，并对其进行几何清理，采用三角形单元进行结构网格划分，网格单元边长平均为4 mm；再次，对机油液面也采用三角形单元进行结构网格划分，网格单元边长平均也为4 mm，进而与油底壳液面以下的结构网格组成一个封闭的空腔，基于该空腔网格生成机油的四面体单元结构网格；最后，把机油的结构网格转化为流体网格，并在流体网格自由液面处施加声压值为零的边界条件，同时把多余的结构面网格(机油液面)删除，为保证计算精度以上网格均需转换成二级精度，至此完成耦合有限元模型的建立，并保证了耦合面上结构网格与流体网格的节点相对应。

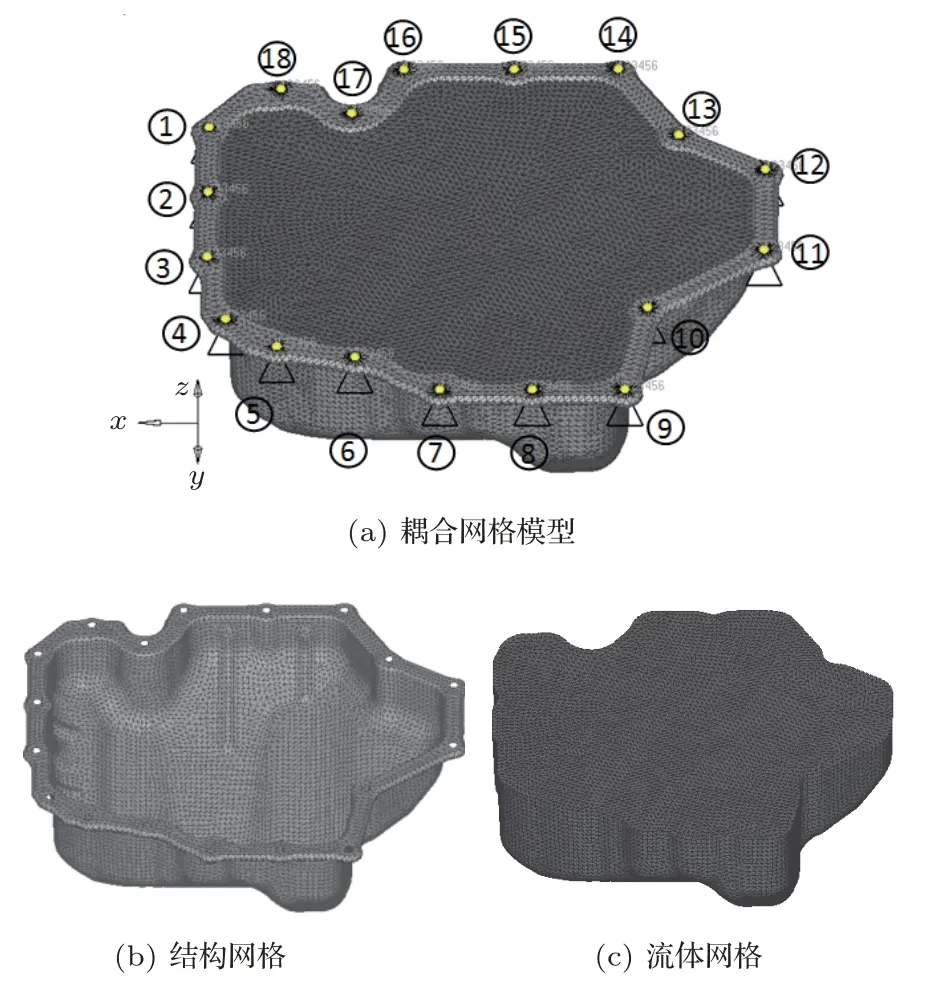
图1 耦合有限元模型Fig.1 Coupled finite element model

由于油底壳属薄壁壳体类零部件，其刚度较弱，当与刚度较大的零部件(缸体)螺栓连接时，可以将螺栓孔处简化为节点，对其进行固定约束，其建立的耦合有限元模型和螺栓孔节点编号如图1所示，网格单元参数如表2所示，结构材料参数如表3所示，流体声学参数如表4所示。为了方便后续结果间对比与说明，使用发动机坐标系(+x：沿飞轮端指向正时端，+y：排气面指向进气面；+z：沿缸筒指向发动机上端)进行定义[8]。

表2 网格单元参数Table 2 Mesh element parameters

表3 结构材料参数Table 3 Structure material parameters

表4 流体声学参数Table 4 Fluid acoustic parameters

2.2 耦合模型试验校核

为验证耦合有限元模型的合理性，把发动机整机用弹簧悬挂起来使其处于自由状态下，选用LMS Test.Lab试验模态分析系统，采用锤激试验法，激励xyz三个方向进行油底壳的约束模态测试，分析带宽为4096 Hz，分辨率为1 Hz，数据进行5 次平均采集。试验测试如图2所示。

把前面建立的耦合有限元模型，导入到求解器中进行约束模态计算，为了保证强迫响应计算准确性，模态计算截止频率内的模态阶数应大于强迫响应计算截止频率内模态阶数的两倍，本文耦合计算关注频率为3000 Hz内，对应耦合模态阶数为25阶，结构及流体模态计算阶数分别设为50阶，满足模态截断原则。

耦合模态频率的测试和计算结果对比情况如表5所示；耦合模态振型的测试和计算结果对比情况如图3所示，颜色越深表示相对变形量越大(左侧为测试结果，右侧为计算结果)。

结果对比显示，耦合模态振型相互对应，模态频率差值在10%以内，可以认为油底壳耦合模型基本正确，可以用于后续分析。

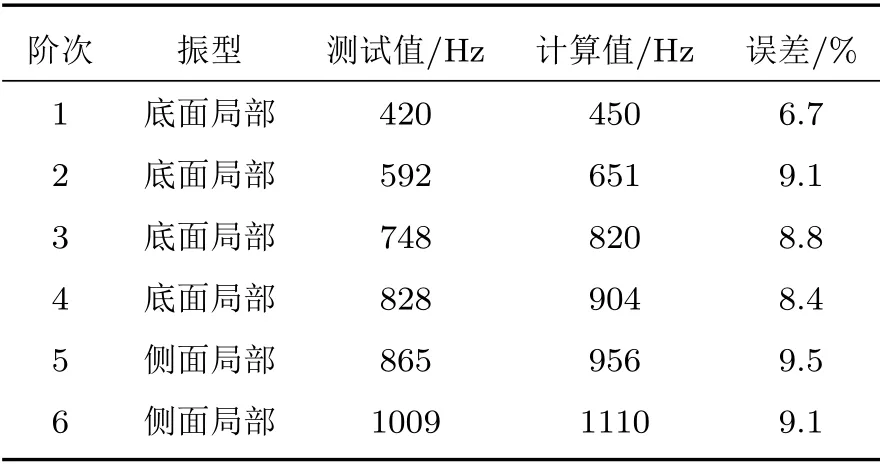
表5 模态频率对比Table 5 Modal frequency comparison

2.3 含油量对油底壳耦合模态的影响

由于发动机的机油含量会在一定范围内变化，为考虑不同机油含量对油底壳耦合模态的影响，本文在前面建立的耦合有限元模型基础上，把机油的含量分别设为无机油、1/4 和1/2 状态进行计算，并和满油状态进行对比，满油状态为发动机运行时的理想状态，如表6所示。在发动机实际运行时，油底壳为倾斜状态，当超过1/2 时油液液面无法准确测量，模态试验误差大，只进行油底壳机油含量为无机油、1/4、1/2和满油状态的模态和辐射噪声计算。

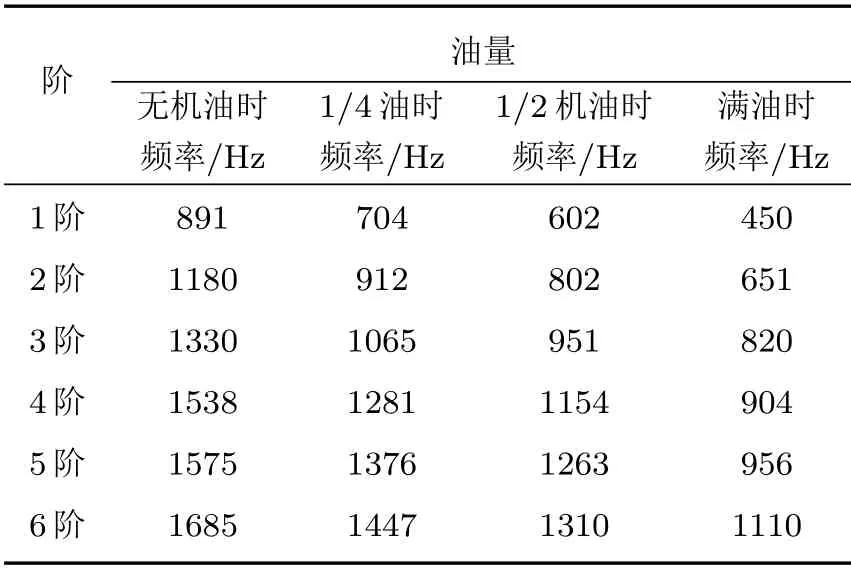
表6 含油量对模态频率影响Table 6 Influence of oil content on modal

由表6 对比结果可以看出，模态频率随着机油含量的增加逐渐下降，模态阶数越高频率下降值存在变大趋势，可看出机油含量对高阶模态影响更大一些，模态频率差值最大达到49%，可见机油与油底壳之间的耦合作用对模态影响是不容忽略的[9]。

3 油底壳流固耦合振动噪声预测分析

3.1 试验设计

油底壳通过螺栓与发动机曲轴箱的下表面相连接，发动机作用在曲轴箱上的激励，会通过曲轴箱的下表面传递给油底壳[10]，同时，在除螺栓孔外的接触面上存在密封胶，起到隔振作用，可近似地认为仅通过螺栓传递激励，所以，可按图1所示在螺栓孔节点上施加激励载荷进行计算。目前，激励载荷的获取方式主要有三种，一是通过多体动力学软件计算获取激励载荷[11]；二是通过经验公式推导获取标准激励载荷[12]；三是在发动机工作过程中，测量连接螺栓上的振动加速度信号作为激励载荷。

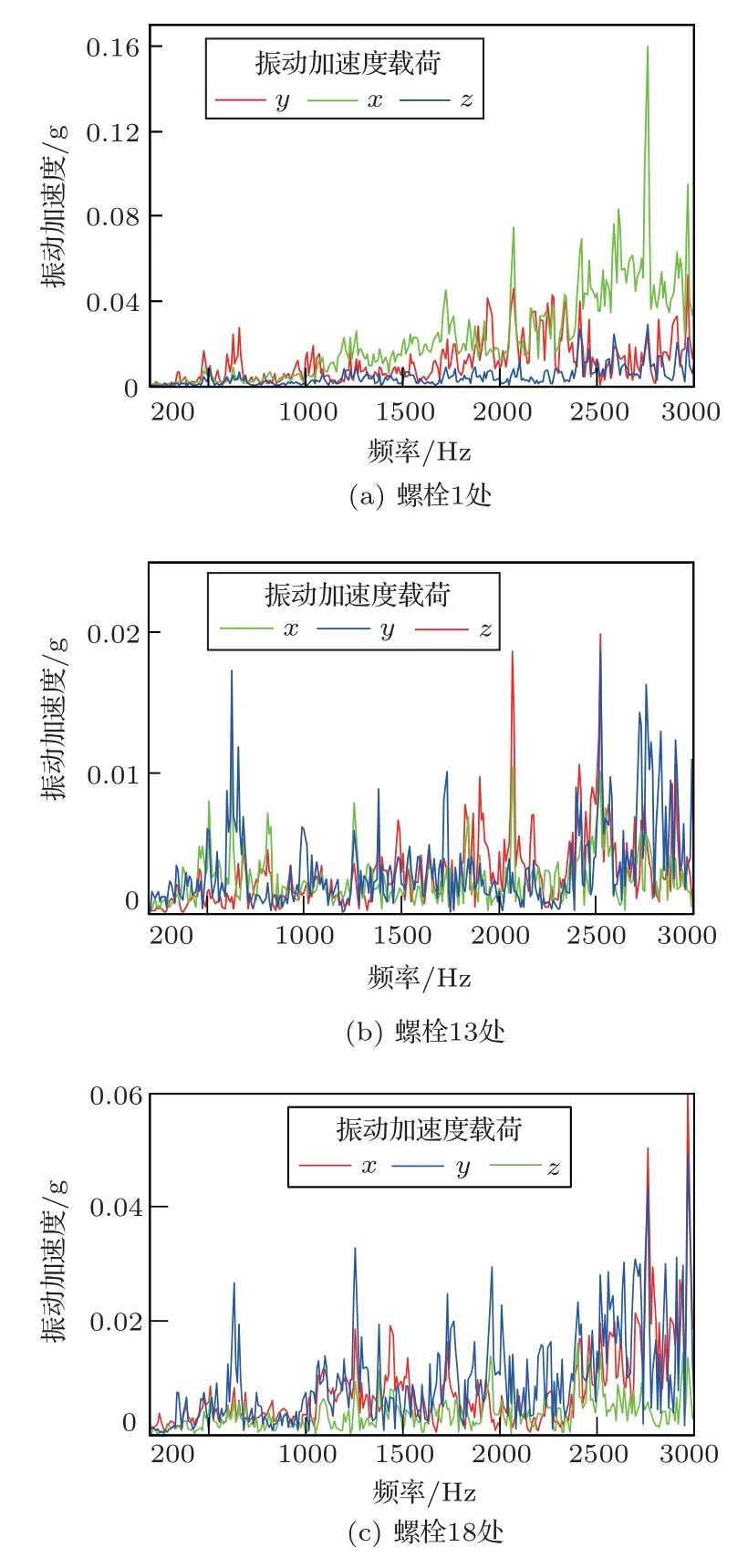
图4 螺栓处振动加速度载荷Fig.4 Vibration acceleration load at bolt

本文在发动机转速900 r/min、空载工况下实际测量所有连接螺栓上3 个方向振动加速度信号作为激励，直接把采集的振动加速度信号施加到对应的节点上(如图1(a)所示)计算油底壳的振动响应，每秒采集10次数据，把螺栓1～18点激励数据转换成频谱图，输出UNV 格式文件(该格式可直接输入到LMS Virtual Lab 中计算强迫振动)，限于篇幅限制，在此仅列出1、13、18(编号如图1(a)所示)三个点的振动加速度载荷，频率范围为100～3000 Hz，如图4所示。同时，测取油底壳底面处的振动加速度响应和底面30 cm近场的声压级作为试验校对数据，测点位置如图5和图6所示。

图5 油底壳底部振动响应点位置Fig.5 Position of vibration response point at bottom of oilpan

图6 油底壳底部30 mm 麦克风测点Fig.6 Microphone measurement point 30 mm from the bottom of oilpan

3.2 强迫振动分析及试验对比

由于计算辐射噪声的边界元模型是以结构有限元的强迫振动分析结果作为输入边界，为此需先对油底壳的进行强迫振动特性计算。首先，把耦合模态计算结果导入到LMS Virtual Lab计算软件中，在该软件中生成流固耦合交互面；然后，把试验测得的所有螺栓处的振动加速度载荷施加到对应的节点上，进行基于模态的耦合强迫振动计算，设置计算频率带宽为100～3000 Hz，分辨率为1 Hz，输出所有点的振动加速度响应；最后，将图5所示三处响应点的振动计算结果与测试结果进行比较，比较结果如图7所示。由对比结果可见，计算结果与测试结果差异率较小，这就保证了辐射噪声计算的准确输入，同时可以认为采用油底壳连接螺栓处的加速度载荷作为强迫振动分析的激励是可行的。

油底壳上所有点作为响应点，输出振动加速度云图，400 Hz时振动云图如图8所示。

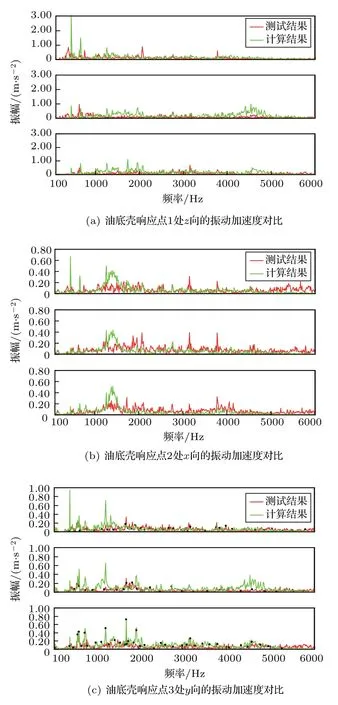
图7 响应点振动加速度对比Fig.7 Comparison of vibration acceleration at response point

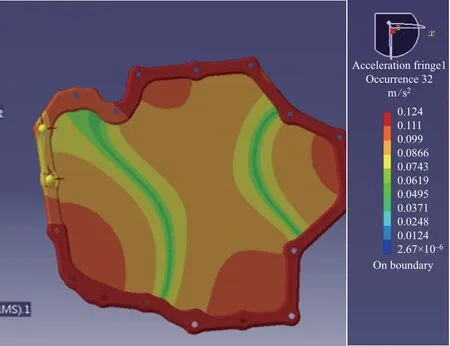
图8 400 Hz 时的振动加速度云图Fig.8 Vibration acceleration color map at 400 Hz

3.3 辐射噪声分析及试验对比

油底壳与安装机体形成一个内部封闭腔，内部声场被封闭，所以，计算辐射噪声时，只考虑指向油底壳外部振动的影响，采用直接边界元法计算油底壳的外部声场。同时流体网格的最大单元增至6 mm，满足声学计算最大单元边长小于计算频率最短波长的1/6 的要求[5]。其中，生成的边界元网格，如图9所示；与试验测点相对应，在油底壳下方30 cm处设置一个声压场点网格，如图10所示；以模型中心为圆心，半径为1 m，生成声功率场点网格，如图11所示。

图9 边界元网格Fig.9 Boundary element mesh

图10 声压场点网格Fig.10 Sound pressure field point mesh

图11 声功率场点网格Fig.11 Sound power field point mesh

把油底壳表面振动响应映射到边界元网格上，计算100～3000 Hz 范围内的油底壳外部声场，得到底部近场30 mm处场点声压级，与试验结果对比，如图12所示。结果显示，1000～3000 Hz 内误差基本在10%以内，均方根(Root mean square,RMS)计算值为60.04 dB(A)，测试值为63.98 dB(A)，差值较小，表明该预测分析方法是可行的。

图12 声压级对比Fig.12 Comparison of sound pressure level

4 含油量对辐射噪声的影响

含油量的多少会使油与油底壳的耦合作用发生变化，影响模态频率和辐射噪声。基于前文含油量不同的模态计算结果和辐射噪声分析思路，计算含油量分别为无机油、1/4、1/2 和满油时油底壳外部声场，得到其声功率级频谱，如图13所示。

由图13 可知，无机油、1/4 油、1/2 油和满油时，总声功率级分别为70.1 dB(A)、60.31 dB(A)、58.93 dB(A)和55.94 dB(A)，大小依次降低，说明结构和油的耦合作用可使结构振动噪声减少，油可以起到减振降噪的效果，含油量越多效果越好。

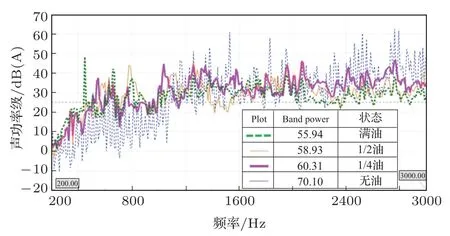
图13 声功率对比Fig.13 Comparison of sound power

5 结论

通过对含油状态油底壳的模态测试校对，验证了油底壳流固耦合有限元模型的准确性；通过对强迫振动计算结果的试验对比，保证了噪声计算结果对比的可信度，主要对比结论如下：

(1)机油与油底壳之间的耦合作用对模态影响是不容忽略的。耦合模态频率随着机油含量的增加逐渐下降，模态阶数越高频率下降值存在变大趋势；机油含量对高阶模态影响更大一些，模态频率差值最大达到49%。

(2)油底壳底部近场30 cm处场点声压级，频率段1000～3000 Hz 的计算与试验曲线基本吻合，该方法用于预测分析不同方案噪声，可指导设计。

(3)结构和油的耦合作用可使油底壳结构振动噪声减少。随着油底壳含油量的增加，声功率级逐渐降低，机油可以起到减振降噪的效果，含机油量越少噪声辐射越大。