水下对转螺旋桨流致辐射噪声机理与预报方法*

曾 赛 杜选民 范 威

(1 水声对抗技术重点实验室 上海 201108)

(2 上海船舶电子设备研究所 上海 201108)

0 引言

对转螺旋桨是指分别安装在具有相同轴心的外轴和内轴上、正反转动的一对推进装置，由于其具有可减轻桨叶推进载荷、提高推进效率、消除扭矩等突出优点[1-2]，被广泛用于航空、航海领域，如对转翼飞机、鱼雷、潜艇、油轮、商船、UUV 等，表1给出了采用对转螺旋桨作为推进器的典型航行体。

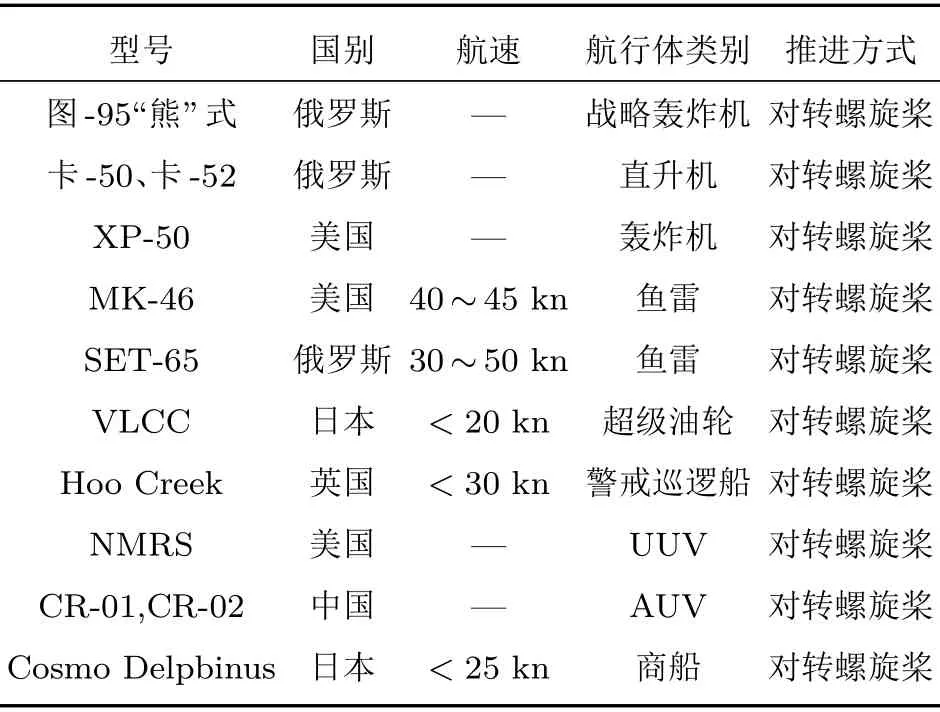
表1 采用对转桨作为推进器的典型航行体Table 1 Typical vehicles which use counterrotation propeller

随着对平台舒适性、隐身性、探测识别需求的不断增加，对转螺旋桨辐射噪声在航空和航海领域得到高度关注[3]。事实上，对于对转螺旋桨流致辐射噪声的研究具有非常广泛的工程背景需要，并且自20世纪20年代螺旋桨声学[4]建立开始便一直是研究的热点之一。对转螺旋桨噪声本质上是流致噪声，是由桨叶与附近的流体相互作用引起[5]，从能量守恒的角度而言，对转螺旋桨的部分动能以声能的形式辐射到介质中形成辐射噪声，对转螺旋桨辐射噪声的研究是伴随着流致噪声的研究而展开的。从20 世纪初开始，流致噪声的机理、预报与控制研究活跃至今并取得巨大进步，最具代表性的是Lighthill[6]气动声学理论的建立，作为独立的学科分支，气动声学无论在理论还是实践应用上均取得了丰硕成果。

航海领域中的“水动力声学”与航空领域中的“气动声学”存在介质上的巨大差异，且研究起步较晚，虽然气动声学的研究方法可以移植到航海领域，但二者的研究重点与噪声特性存在显著不同。本文拟尝试以流致噪声发声机制作为依托综述水下对转螺旋桨的流致噪声机制与预报方法，为水下航行体的目标探测与识别提供支撑。

1 水下对转螺旋桨流致辐射噪声机制

水下对转螺旋桨是典型的旋转机械，对转桨工作时，前后桨旋转方向相反，使得附近流场非常复杂，其辐射噪声主要由附近流体与桨叶相互作用而形成。此相互作用可以概括为：非均匀进流与前桨导边相互作用、桨叶面附近大尺度涡对桨叶非定常诱导力作用、前桨叶面二次非定常流对后桨作用、后桨抽吸作用形成的非定常压力场与前桨相互作用、前桨梢涡脱落与后桨导边相互作用、前桨随边尾涡脱落与后桨导边相互作用、前桨桨毂尾涡及边界层流与后桨相互作用[5]，文献[5]将上述作用分为两种效应，即前后桨干涉效应和谐波流场效应，如图1所示，为前后桨干涉效应的示意图。从流致发声的角度来看，流场与结构之间的相互作用是水下对转螺旋桨流致发声的根本原因。本文从3 个角度对水下对转螺旋桨流致噪声产生机制与研究进展展开综述，即由运动壁面影响的湍流噪声、旋转噪声和水动力空化噪声。

图1 对转桨干涉效应示意图Fig.1 The interference effect of counter-rotation propellers

1.1 运动壁面影响的湍流噪声

水下对转螺旋桨的湍流脉动是其主要水动力噪声源之一，如何在水下对转螺旋桨复杂的流场中准确描述其声源是湍流噪声预报的关键问题。水下对转螺旋桨的运动属于低马赫数运动，在低马赫数下，自由流场中的湍流声辐射效率非常低，在远场条件下可以忽略不计，而在非自由场中，壁面的存在可以大幅增加流体发声的效率[7]，主要表现在：首先壁面(对转螺旋桨的随边)的存在会有涡脱落现象，这会产生或者增强辐射特性；其次，壁面的边界层分离也会产生或者增强辐射特性；再者，壁面的存在会对已经形成的辐射噪声产生反射效应，而且壁面附近的湍流导致流动非均匀性会提高流声转换效率[8]。

将水下对转螺旋桨桨叶的湍流边界层作为辐射声源时，需要准确地模拟边界层上的湍动压力。事实上，边界层湍动压力的建模一直是计算流体力学领域的热点与难点[9]。对湍动压力建模的思路通常借鉴声类比理论。Lighthill声类比理论[6]是描述流体发声的基本理论，其表明流动中的速度脉动、粘性应力和熵波动之间的非线性相互作用产生的非定常流会导致流体密度扰动，从而产生辐射声源。然而Lighthill 声类比理论最初的形式不适合有固体边界存在时的流体发声问题，Curle[10]考虑到了壁面存在对湍流噪声的影响，利用自由场格林函数给出了壁面边界影响的湍流辐射噪声Curle 解。事实上，Curle 方程能够从机理上解释水下对转螺旋桨的湍流发声机制，是研究壁面存在时流致噪声预报的基础，水下对转螺旋桨工作时，其壁面属于运动壁面，对壁面边界运动时的流致噪声预报具有重要的理论与工程意义。最具启发意义的工作来自于Lowson[11]，其首先研究了自由场中运动奇点的辐射声场特性，该工作具有一般性，因为奇点可以表征为单极子、偶极子或四极子。随后Lowson 等[12-13]将成果应用于工程问题的解决之中并取得较好效果。利用广义函数法将Curle 方程解形式推广即得到了FW-H 方程[14-15]，该方程从理论上表明运动壁面边界附近的声源由四极子(湍流应力)、偶极子(脉动压力)和单极子(位移)组成，由于FW-H 方程具有鲜明的物理意义，因此得到了广泛的应用[16]。事实上，作为传声介质的流体自身运动也会对流致声辐射产生影响，将广义格林函数应用于Lighthill方程即得到Goldstein 方程[17-18]，该方程将运动介质和运动壁面因素考虑进来，能够全面客观地对运动壁面流致发声问题进行描述，Curle 方程以及FW-H 方程均是该方程的特殊形式。正是由于Goldstein方程具有物理意义鲜明、约束条件少的优点，其广泛应用于流致噪声的预报之中，水下对转螺旋桨的流致噪声预报亦基于该理论[5,19]。

水下对转螺旋桨运动桨叶壁面的湍流边界层脉动压力亦是重要的近场辐射声源，事实上，湍流边界层中的脉动压力预报一直是流致辐射噪声研究的重点。由于湍流的复杂性，湍流边界层中的脉动压力很难通过数值积分得到，这就限制了Curle方程的应用。为了明确湍流边界层脉动压力的声源属性，Powell[20]将法向速度梯度格林函数应用于Lighthill 方程变形，研究表明湍流边界层中的法向脉动压力属于四极子属性，即Lighthill 应力，而切向的脉动压力数据偶极子属性，也就是说，在湍流边界层脉动压力中，切向的脉动压力才是主要辐射声源，然而关于切向脉动压力是否为有效声源，在学术界却一直存在争议[21-23]，焦点在于湍流边界层脉动压力是直接辐射声源还是由其激励弹性结构形成的二次声源。事实上，这涉及到如何理解与应用Lighthill声类比理论的问题。在湍流边界层脉动压力的预报中，另一个重要的问题是湍流边界层脉动压力的描述，大量的学者进行了卓有成效的研究[24-32]，通用的方法是利用统计湍流理论，采用脉动压力——波数谱定量描述湍流中的时空随机脉动，该理论的基础来自于试验数据的支撑[32]。

水下对转螺旋桨的桨叶在运动时会伴随有涡的脱落，脱落涡的能量来自于桨叶动能，有规律和节奏的涡脱落会诱导产生声源，是水下对转螺旋桨湍流噪声的一部分。关于涡的产生、发放与估计在流体力学中研究广泛，而关于涡声辐射研究较少，奠基性的工作来自于Phillips[33]，其将涡声辐射声强表征为其横向尺度与纵向尺度函数，并通过试验验证了理论模型。此后，Ross[34]发展了Phillips 的工作并给出了涡声转换效率表达式。Powell则针对等熵流动建立了涡声理论，涡声理论表明流体中的声波产生与其中的涡、势流以及二者的相互作用有关，声辐射是通过非线性相互作用完成的。此后，许多学者在涡声理论进行了大量的工作[35]。涡声理论为水下对转螺旋桨的流致尾涡发声提供了预报理论依据。但需要注意的是，涡声理论由于方程的非线性，尚无法与具有重大工程应用价值的声类比理论相比。

1.2 旋转噪声

水下对转螺旋桨属于典型的旋转机械，与气动声学领域中的旋翼类似，其发声均属于旋转噪声研究范畴，虽然从发声本质上来讲，水下对转螺旋桨的旋转噪声属于运动壁面的湍流噪声，但考虑到旋转噪声具有鲜明的工程背景，且工程界有针对性地进行了大量的研究，因此对其旋转噪声预报方法进行总结。

正如1.1 节分析，在水介质中的对转螺旋桨运动均属于低马赫数运动，在声远场条件下，考虑到四极子的辐射效率在低马赫数下非常低，因此在工程预报中通常可以忽略四极子效应。此时，在非空化条件下，水下对转螺旋桨桨叶壁面的湍流边界层脉动压力呈现偶极子属性，辐射效率最高，是主要辐射声源。在空化条件下，水下对转螺旋桨桨叶附近的空泡是主要辐射声源，将在1.3节中进行阐述。水下对转螺旋桨旋转噪声本质上是由前后桨相互干涉引起[5]，类似于转子-定子的相互作用，事实上，二者在发声机制上没有本质的区别。在转子-定子的发声机制上，国外学者进行了大量的研究[36-40]，研究表明转子-定子机构的相互作用可以用势流作用和粘性作用来描述，其中粘性作用是导致转子-定子机构发声的原因，即转子的粘性尾流冲击定子叶片形成宽带噪声谱。Hanson[40]的研究则表明，转子-定子机构的布置顺序不影响宽带噪声谱特征。基于广泛的工程学背景，转子-定子更精确的发声特性被发现，如低频线谱形成、管道对转子- 定子声辐射影响以及转子-定子几何参数对于声辐射特性的影响等[41-44]。

水下对转螺旋桨旋转噪声的分析思路与转子-定子机构噪声分析基本一致，理论上借鉴简化形式下的Goldstein 方程——FW-H 方程。以非空化工况为例，水下对转螺旋桨辐射噪声的预报思路[45]是：首先通过计算流体力学方法(Computational fluid dynamics,CFD)获取前后桨叶上的非定常力，然后将非定常力作为声源项代入FW-H 方程右端，利用Kirchhoff方法求得水下对转螺旋桨非空化远场辐射声压。在该思路中，相互作用下前后桨叶上的非定常力预报成为关键。事实上，学术界和工程界对于螺旋桨旋转噪声的预报均采用这种思路，代表性的工作来自于朱锡清等[19,46-47]，他们用这种方法分别建立了单桨和对转螺旋桨的旋转噪声预报模型，前期的考虑是将螺旋桨载荷的谐波系数作为计算辐射声源的依据，此后又采用升力面理论得到桨叶表面的非定常力作为声源，相比之下提高了声源提取的精度，据此分析了螺旋桨固有的几何参数对于旋转噪声的影响。基于进一步提高桨叶表面非定常力提取精度的考虑，面元法被用于提取桨叶表面的非定常力[48]。时域FW-H 方程虽然方便进行数值解析，但存在物理意义不明确的缺点，这对于解释螺旋桨辐射噪声产生的原因不利，基于此，Hanson[49]通过对时域FW-H 方程进行傅里叶变换得到了频域内螺旋桨辐射噪声计算公式，并且推导得到了航空对转螺旋桨辐射噪声频域预报公式。Hanson公式具有非常明确的物理意义，能够在公式中定性分析螺旋桨几何参数对于辐射噪声的影响[50]。国内学者正是基于Hanson 的思想，给出了螺旋桨桨叶非定常力源在频域中的处理方法，并针对水下对转螺旋桨进行了旋转噪声预报[5,19,51]。

1.3 对转桨空化噪声

对于水下对转螺旋桨而言，空化噪声是非常重要的噪声源，一旦出现空化，空化噪声往往会占据统治地位。对转螺旋桨的空化噪声来源于桨叶附近空化泡的生成与溃灭，空化泡的溃灭会产生高速射流不断冲击桨叶壁面形成空蚀，由此发出强烈的辐射噪声，空蚀噪声一方面来源于空泡的破裂，另一方面来源于桨叶壁面的声反射效应。空化泡的生成与溃灭会引起桨叶表面的流体体积变化，从声类比的角度而言属于单极子属性。

对转螺旋桨的空化噪声本质上属于水动力空化噪声，对于水动力空化噪声的研究具有重要的理论与工程意义。国内外学者对于空化噪声从理论和试验的角度进行了大量的研究。最早的尝试来自于Reyleigh[52]，但其建立的理想球形空泡运动方程无法描述很小半径的空泡溃灭过程，此后，Plesset 等[53]、Noltingk 等[54]、GilmoreI[55]修正了理想球形气泡模型。进一步的研究来自于Benjiamin 等[56]，其建立了非球形空泡的运动控制模型，但该模型对于大变形的空泡无法准确描述。

对于水动力空化噪声更具有工程意义的研究是对于有壁面影响的空泡溃灭噪声进行研究。然而由于问题的复杂性，尚没有对于该问题的解析理论。常用的方法主要是数值计算方法[57-60]。水下对转螺旋桨空化噪声属于典型的有壁面影响的空化噪声，国内学者王顺杰等[51]尝试使用声类比理论建立水下对转螺旋桨的空化噪声模型，基本的考虑是将Goldstein 方程右边的四极子和偶极子源项忽略，将空泡简化为单极子模型，通过求解简化的Goldstein 方程给出对转螺旋桨空化噪声解。分析表明，在空化状态下，线谱幅度与宽带噪声幅度差别减小，空化噪声整体噪声级提升。曾赛等[61]通过空泡水筒试验测量了对转螺旋桨的空化噪声，并观察了空泡形成的过程。许多新的手段也被用于空泡噪声形成机制的研究，如电解泡、火花泡、激光泡以及声全息照相技术等[62-67]。

1.4 水下对转桨流致噪声预报方法

1.1～1.3 节综述了水下对转螺旋桨流致辐射噪声预报的进展，无论是湍流噪声、旋转噪声还是空化噪声，建立流致辐射声源项是关键，声源的提取与计算主要有3 种方法，即声类比理论[68]、Kirchhoff理论[69]和涡声理论[70]。3种方法的比较如表2所示。

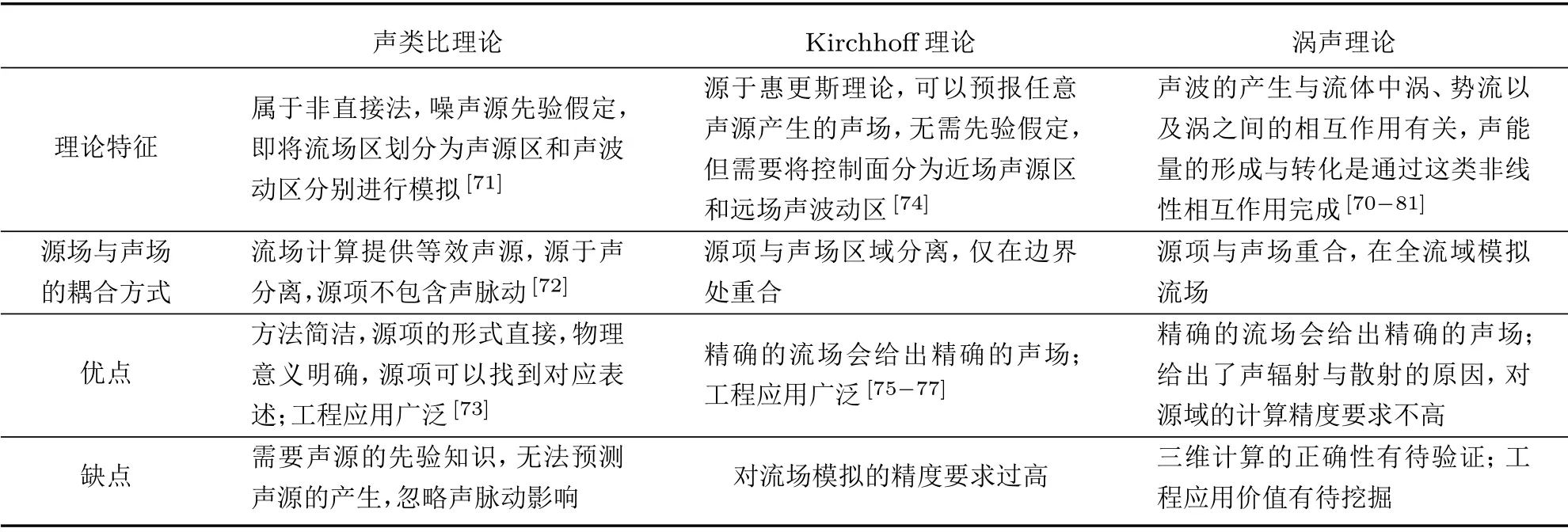
表2 声类比理论、Kirchhoff理论和涡声理论比较Table 2 Comparison of acoustic analogy,Kirchhoffmethod and vortices-induced noise theory

2 水下对转桨流致噪声数值预报方法

2.1 对转桨流致噪声数值预报的难点

数值计算方法是对水下对转螺旋桨流致辐射噪声进行预报的重要方法，得益于计算机计算能力的飞速发展，对流场进行大规模数值模拟成为可能，这就为声源项的提取提供了有力的方法。考虑到流场与声场的量级差别，对转螺旋桨流致噪声的数值预报面临着许多难点[82]，主要表现在：

(1)非线性效应影响。对转螺旋桨的流致辐射噪声是非线性、非稳态的过程，依赖于N-S方程的流场预报通常是非线性的，而声传播的过程则无需考虑非线性，如何将这种线性与非线性问题统一进行考虑是需要解决的难点。

(2)流动能量与声能量之间的量级差别巨大。通常流体动能远远大于的声能量，导致声场的幅度远小于湍流脉动的幅度，在数值计算值中要保证声场的计算精度则需要数值误差小于声场幅度，这对于计算资源形成了巨大的挑战。

(3)计算噪声的带宽选择。非定常流场模拟的步长决定了声场频率的分辨率，如果需要计算宽带噪声，则需要足够小的时间步长，这对于数值模拟资源形成巨大的挑战。

(4)声场与流场的传输特性差异[83]。流场中的声辐射传播具有各向同性，无色散、无耗散，而流场中的涡传播则是高色散、高耗散的，且数值模拟的流场也是色散的，这样就无法保证声场计算的精度，需要专门的色散保持方法解决该问题。

(5)边界条件的选择[84]。数值计算的有限区域与流致发声的无边界区域存在矛盾，通常需要在人工区域的边界上赋予边界条件，但边界条件导致的虚假数值反射误差与声场能量处于同一量级，使得数值预报的声场缺乏精度，因此通常需要采用无反射边界条件。

事实上，上述数值计算困难是气动声学与流体声学共同面临的难点[85]，水下对转螺旋桨流致噪声的数值模拟方法完全可以借鉴气动声学领域成功的经验。

2.2 直接数值预报方法

所谓直接数值预报方法(Direct numerical simulation,DNS)是指利用N-S 方程直接求解水下对转螺旋桨的流场与声场。直接预报方法的突出优点是其不受流动状态以及声源属性的限制，能够直接给出流致噪声的产生与传播特性，特别适合模拟宽频段的流致辐射噪声。但需要注意的是直接数值模拟需要考虑流场的所有湍流尺度，而声场与流场的能级差别巨大，如何从流场中提取出声场脉动是一个巨大的挑战。直接数值模拟方法在低马赫数时难以给出远场声辐射计算结果，计算资源受到极大的制约。事实上，直接数值模拟只在气动声学这一类高马赫数工况下取得了成功[86-88]。可以设想，采用直接数值模拟方法求解水下对转螺旋桨这一类低马赫数旋转机械的流致噪声会面临巨大的困难。

为了避免直接数值模拟的困难，工程中一个折衷的办法是采用大涡模拟方法(Large eddy simulation,LES)对流致噪声进行数值求解，该方法较好地平衡了计算成本与收益[89]。但需要注意采用低色散、低耗散、高精度的数值格式和低耗散、高精度的亚格子模型，还需要确保所画网格分辨率能够分辨所有频率的辐射声波[90-91]。

综上所述，采用直接数值预报方法模拟水下对转螺旋桨流致辐射噪声的一般过程可以概述为：首先使用直接数值模拟或大涡模拟方法求解对转螺旋桨近场流场，然后在远场划分一定精度的网格，在近场与远场的边界上给出无反射边界条件，使用简化的线性控制方程求解远场辐射声场。一般而言，只要流场计算得足够精确，那么远场声辐射的计算结果便是可信的。

2.3 间接数值预报方法

所谓间接数值模拟方法，是指将流场与声场的计算分开，忽略流场与声场的耦合性，先进行流场的模拟，然后进行声场的模拟。声类比理论和Kirchhoff理论为间接数值预报方法奠定了理论基础。按照声类比理论的观点，只需要在流场中找到声源项便可以进行辐射噪声的模拟，声源项是先验的，只需要精确地模拟流场，提取出声源项便可以使用古典波动声学预报流致辐射声场[92-93]。从这个角度而言，间接数值预报方法具有重要的工程应用价值。

由于水下对转螺旋桨工作的介质为低马赫不可压缩流体，流体的惯性特征占据主要位置，可以忽略流场对声场的影响，近场流场的计算可以采用不可压缩流场控制方程预报，因此特别适合声类比理论进行流致辐射声场的预报[94]。事实上，国内很多学者利用声类比理论间接数值预报方法对水下对转螺旋的流致辐射噪声进行了预报，代表性的工作来自于朱锡清等[19,46-47]，其利用升力面理论预报了流场中对转螺旋桨的脉动压力，以此作为声源项给出了水下对转螺旋桨的远场声辐射特性，并通过试验验证了数值计算结果。王顺杰等[51]则利用CFD 方法模拟了流场中的脉动压力，并通过FW-H 方程计算了对转螺旋桨的近场辐射噪声。曾赛等[45]则利用耦合数值方法预报了水下对转螺旋桨的无空化线谱辐射噪声。常欣等[95]亦利用耦合数值方法分析了对转螺旋桨几何参数对于无空化辐射噪声的影响。王顺杰等[96]研究了片空化对于对转螺旋桨空化噪声的影响。此外，国内外学者基于间接数值预报方法各种旋翼以及水下航行体流致噪声进行了研究[97-103]，为实际的工程问题解决提供了参考。

3 结论

水下对转螺旋桨广泛用于各种水下与水面航行体，水下对转螺旋桨流致噪声产生机制以及预报方法的研究对于水下/水面目标的特性分析以及探测识别具有重要的意义。本文对水下对转螺旋的流致辐射噪声产生机制以及预报方法进行了综述。水下对转螺旋桨的流致辐射噪声本质属于水动力噪声，可以借鉴气动噪声的研究方法，但需要注意介质属性的不同会导致水动力噪声与气动噪声的研究侧重点不同。声类比理论、Kirchhoff理论和涡声理论能够较好地解释水下对转螺旋桨的流致辐射噪声的形成机制。数值模拟是进行水下对转螺旋桨流致辐射噪声预报的有效方法，但直接数值模拟会存在计算效率与成本不匹配的缺点，基于声类比理论的间接数值模拟方法是工程预报水下对转螺旋桨流致辐射噪声的可行方法，但需要注意流场模拟的精度直接影响辐射声场的模拟。尽管如此，水下对转螺旋桨流致辐射噪声的预报仍然面临许多问题，如发声机制有待进一步深入研究、数值计算精度有待提高、计算效率有待提高、噪声源项对于整体辐射声场贡献的区分以及本征声特征量的提取等。需要紧跟当下水动力噪声预报最新进展，发展水下对转螺旋桨的流致辐射噪声预报理论和数值计算方法。