利用噪声互相关技术计算福建台网台站绝对钟差

胡梦迪 ，金 星 ，李 军

（1.中国地震局工程力学研究所，黑龙江 哈尔滨 150080；2.中国地震局地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080；3.福建省地震局，福建 福州 350003）

0 引言

地震记录的时间准确性对一些时间精度要求较高的地震研究至关重要，特别是对于地震预警、地震定位以及地壳结构层析成像等研究。地震台站授时主要由两部分完成，一是通过GPS（全球定位系统）进行授时，二是由地震观测设备自带的晶振计时。一般而言，台站定期接收GPS授时信号，时钟稳定，然而GPS信号会受到雷雨等不良天气或是GPS模块故障的影响导致无法通过外部授时信号校正时间，此时只能依靠内部晶振计时[1]，而晶振易受温度、湿度等因素影响导致计时偏差。因此，钟差是实际工作中经常遇到的问题，如何判别钟差是一项重要工作。

目前，钟差判别通常是基于地震事件定位得出台站走时残差。此方法需人工标注震相，依赖于工作人员的经验和地震事件的发生以及地震事件的大小。由于远震震相往往不够清晰导致无法准确标注，因此一般只适用于近震。同时，该方法只能判别出地震事件发生时有无钟差，无法得知钟差起止时间。可见利用地震时间判别钟差的方法所受限制因素较多。

Derode等[2-3]发现台站间背景噪声的互相关格林函数与真实格林函数只有幅值上的差异，而在相位上是一致的。而在钟差研究中，我们关注的核心也是相位变化，由此可利用背景噪声互相关研究钟差。Stehly等[4]用11年的连续记录提取面波格林函数，用噪声互相关方法分析了位于加利福尼亚南部的三个宽频台站对（PAS-PFO、GSC-PAS、PFO-GSC） 的互相关函数走时信息，计算出台站绝对钟差；Schönfelder等[5]在对Merapi火山台阵的研究中，通过重建格林函数，构建相对钟差超定方程组求得台阵中四个台站的绝对钟差。P.Gouédard等[6]分别利用基于背景噪声互相关技术的时间对称分析法和虚拟重复地震法校正OBS（海底地震仪）时钟，结果表明OBS时钟不论是线性还是非线性漂移都可以通过背景噪声互相关计算得到。郑宏等[7]基于背景噪声互相关技术校正雅浦俯冲带OBS时钟，分别进行了线性校正和考虑钟差闭合性的计算。

本文利用背景噪声互相关技术就2018年福建省地震台网单台钟差进行计算，选取每天的格林函数作为短期格林函数。

1 数据及预处理

本文利用福建台网88个测震台2018年的记录进行研究，选取三分量中的竖向分量。88个台站在全省分布大体均匀（图1），台间距主要集中在 50～300km，最大超过 500km（图 2）。

图1 台站空间分布图Fig.1 Station spatial distribution map

图2 台间距分布Fig.2 Station spacing distribution

台站原始地震记录中包含一些对于背景噪声来说是干扰的信号，如地震信号、仪器响应等，为得到纯净的噪声信号，需要对原始数据进行预处理，预处理步骤如下。

1.1 重采样

本文研究的台站其采样率为100Hz，采样率大不利于数据的处理及读取存储，以减少数据点，因此本文进行采样率为5Hz的重采样。

1.2 去均值去趋势

台站记录会受到基线漂移、突跳以及仪器本身的长周期振动的影响，需要去除这类影响，通过去均值处理可以达到目的。去趋势可以消除地震仪器获取数据时产生的偏移对后期计算产生的影响。

1.3 带通滤波

地震信号中不同频率成分包含不同信息。噪声大体上可分为高频（1Hz以上）、低频（1～10s） 及长周期（10～50s） 三部分[8]，其中高频噪声主要受人类活动影响[9]，低频是由于海洋波与海底或海岸线的非线性作用引起的[10]，长周期主要是风、急流等自然因素引起[11]。本文利用来源于海洋性质稳定的低频成分，选取1～10s带通滤波。

1.4 时域归一化

为剔除记录中夹杂的地震信号，需做时域归一化，本文选取滑动窗绝对均值归一化法。给定一个时间序列dj，对于计算时间点n处的归一化权重，计算如下式（1）：

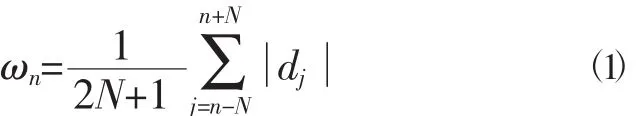
图3波形数据预处理Fig.3 Waveform data preprocessing

图3 中，a为SHLX台2018年11月26日台湾海峡地震竖向分量原始记录波形；b为经重采样、去均值去趋势后的波形；c为1～10s带通滤波后的波形；d为经滑动窗绝对均值归一化后的噪声波形图。

至此，经过以上四个步骤处理后，数据预处理即完成，得到的噪声记录可以用于互相关计算。

2 方法及其原理

2.1 通过互相关函数获取走时信息

一个弥散场中台站A，B的背景噪声记录在时域下的互相关函数C（τ）计算式如下式：

式中u、u*分别为A，B两台记录到的噪声。

噪声源的空间分布及噪声水平只会影响互相关格林函数的振幅[13]。理论上，对于台站A与B，不论其所在场地噪声源是否为均匀分布，AB台站对得到的噪声互相关函数峰值到时总是对称的，背景噪声互相关函数与格林函数在相位上一致，只有幅值上的差异。因此，可利用背景噪声互相关函数提取格林函数。本文选用台站垂直分量计算背景噪声格林函数，垂直分量记录的是瑞利面波，即提取的是瑞利面波格林函数。

图4不同钟差情况时格林函数图Fig.4 Green’s function graph for different clock conditions

图4 中，a为噪声源均匀分布，不存在相对钟差时的互相关格林函数；b为存在正相对钟差时的互相关格林函数；c为存在负相对钟差时的互相关格林函数。虚线代表走时对称轴，具有相对钟差时，对称轴发生偏移。

台站间噪声做互相关，其结果包含台站间相对钟差信息（图5），为提取钟差信息，需要无钟差的格林函数作为参考。钟差是偶尔存在的，长期的噪声互相关结果叠加可以忽略钟差影响，且随叠加时长的增加，互相关格林函数的信噪比会增大，因此本文选取一年叠加（本文将噪声以不重叠的半小时时窗划分，一年叠加即是17520个窗叠加）结果作为参考格林函数。将参考格林函数与短期互相关格林函数再做互相关，得到的互相关函数峰值的位置反映台站间的相对钟差值。左右分支叠加能提高信噪比，本文以两分支叠加的结果计算相对钟差。图5中峰值位置与0s的偏移值即为钟差值，不同颜色代表不同时段的结果。

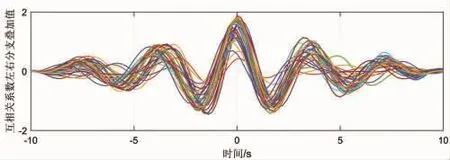
图5 互相关函数左右分支叠加后结果Fig.5 Cross-correlation function left and right branches superimposed results

2.2 求解单台钟差

由2.1节得到各台站间的相对钟差，台站i，j间的相对钟差与绝对钟差可表示为：

其中ΔSi、ΔSj分别为台站i，j的绝对钟差，ΔSi-j为台站i，j间的相对钟差。所有台站间的相对钟差关系可整合成矩阵形式，如式（4），本文方法的核心即是构建此矩阵。

此矩阵简记为Gm=d，其中m是由ΔS1、ΔS2……组成的列向量，即台站1、台站2……的绝对钟差。d是由ΔDS1-S2、ΔDS1-S3……组成的列向量，即台站1与2的相对钟差、台站1与3的相对钟差......。88个台站共组成3828个台站对，因此m的行数为3828行，列数为88列，即台站个数。此方程组为超定方程组，系数矩阵非方阵，所以m不可逆，求解此方程只能借助系数矩阵的广义逆，即m=G+d，寻找其满足最小二乘的解。

3 单台钟差结果

3.1 每日钟差结果

本文以不重叠的，窗长为半小时的时窗将噪声记录进行划分，半小时窗做互相关得到的格林函数信噪比约为1～3，考虑到其信噪比不够高会影响计算结果准确性。信噪比与叠加时长有关，叠加时长越长信噪比越大。为提到信噪比，采用一天内48个半小时窗互相关格林函数叠加作为每天的互相关格林函数，信噪比最大达到21左右。下面以全年无钟差台站AXCK及CTCX、PTDT、ZPLA三个存在明显钟差的台站为例进行分析，其钟差计算结果如图6所示，其中红、蓝、绿、紫红色虚线分别表示1，2，3，4号地震发生时间，灰色部分为误差棒，代表标准差。

图6 每日钟差计算结果Fig.6 Calculated daily clock difference result

验证钟差计算结果的准确性，需要与地震事件得到的走时残差对比。选取四个地震事件，震中位于岛陆和近海，对于此类地震，单纯型法定位优于HYOSAT、LOCSAT法[14]。因此本文用单纯型法定位获得台站走时残差（表1）。

表1 地震事件与走时残差

图6中，四个台都在7月存在断记，可能是由于供电设备故障、数采故障、地震计无输出、通信链路中断等造成，但短时间断记不影响本文研究结果。

对于不存在钟差的台站AXCK，钟差变化幅度不大，年平均钟差在0.0092s±0.1157s范围内波动，无较大突跳，时钟良好。对于存在明显钟差的台站，每日钟差计算结果与地震事件得到的走时残差存在一定偏差，但钟差的线性漂移及突跳都比较清晰地显现出来。如PTDT台在11月23日，每日钟差计算结果为+1.3s，与走时残差+2.0s相差0.7s；在4月份，PTDT台存在约-0.015s/天的线性漂移。

3.2 方法改进

用本文方法求解一个台站数众多的网络中的单台绝对钟差，结果的准确性会受限于互相关格林函数的信噪比，信噪比越大，计算结果越准确。信噪比除了与叠加时长有关外，还与台间距相关，台间距越小信噪比越大。短期互相关格林函数取叠加时长为一天时，台间距50km以下信噪比达到21，台间距300km以上信噪比不及9。台网中有超过500对台站间距大于300km，其互相关格林函数信噪比不够高，求得的相对钟差值不够准确，会对超定方程产生扰动，进而使单台钟差结果存在偏差。

因此本文做出如下改进，为提高台站对信噪比整体水平，选取CTCX台站方圆50km范围内7个台站组成小型网络进行计算，最大台间距85km，最小24km，平均间距48km，取每天的叠加结果作为短期互相关格林函数，此台站网络平均信噪比约21。求解超定方程组得单台钟差结果，CTCX钟差如图7所示。

图7 CTCX台钟差结果Fig.7 Station CTCX clock difference result

2018年5月25日福建漳平地震CTCX台走时残差为-1.0s，CTCX台钟差约-0.9s，两者对应较好；同样6月6日台湾海峡南部地震该台站走时残差为+2.7s，计算钟差约+2.5s，相对误差不及8%，在9月初—12月末是时钟正常的时段，平均钟差为-0.1187s±0.3157s，是可以接受的误差。由此可见，选用间距较近的台站后，得到的结果更加准确。

本文求得福建台网88个测震台2018年全年的钟差变化。总体来看，将时间服务存在故障的台站数按月统计，发现8月与10月两个月存在钟差的台站最多，均为15个，钟差台站数占比不足20%，多数台站时钟正常。时钟偏差有线性漂移与钟差突跳两种形式，多数存在钟差的台站，在钟差突跳或线性漂移结束后都会恢复到正常状态，原因是GPS授时恢复正常或是台站受人工维护。

4 讨论与结论

图6中AXCK台是不存在钟差的台站，但是其计算结果依然存在小幅度波动。王俊等[15]在对江苏省台站钟差计算时同样发现计算结果的小幅波动，进行分析后发现江苏地区夏季噪声源能量优势方向来自太平洋，而冬季则来自于印度洋。考虑到福建省地理位置与江苏省类似，同为东南沿海，同样会受到太平洋与印度洋活动的影响，推测这可能是引起计算结果小幅波动的原因。AXCK台年平均钟差在±0.15s内，在可以接受的范围，不影响对台站时间偏差的评估。在验证钟差计算结果时，最好的办法是与GPS对钟日志进行对比。遗憾的是，GPS对钟日志未被长期保存，在缓存中被不断地刷新，所以无法得到2018年的GPS对钟记录，只能将单纯型法定位得到的走时残差用以验证，虽然精度无法与GPS对钟记录相比，但由于地震事件的发生具有随机性，所以由地震事件定位得到的走时残差还是可信的。

在计算钟差的过程中发现互相关格林函数信噪比对于钟差计算结果的准确性至关重要，如何增大信噪比是提高钟差计算准确性的关键。本文尝试将大的台站网络分为若干个小的网络，如3.2节以CTCX台为中心，方圆50km内的台站组成一个小型网络，使得台网内互相关格林函数信噪比整体水平更高，结果更好。除了选用台间距较近的台站对外，在今后的研究中还可以通过寻找良好的加权方法来提高信噪比。

目前运用此方法能实现精度相对较高的钟差监测，将其整合到地震监测系统上，能提高台网时间服务质量，实现近实时的钟差监测，而且通过历史地震数据可以计算任何时间段任何台站的钟差，不受传统方法的局限性制约。对位于高纬度、山区等GPS信号接收条件不良地区的台站具有重要的现实意义。