基于高斯混合模型的受引导人群疏散研究

刘天宇，杨晓霞，张纪会，赵逸群，周美琦

(1.青岛大学自动化学院复杂性科学研究所，山东 青岛 266071;2.青岛理工大学机械与汽车工程学院，山东 青岛 266525)

0 引言

近年来，行人紧急疏散已经成为一个研究热点，针对行人疏散特点及如何提高疏散效率的研究越来越多。对于行人疏散预案制定的研究已得到世界各地研究机构和政府有关安全管理部门的愈发重视。紧急情况下，在大型公共场所采取正确的疏散战略，可有效减少财产损失和人员伤亡。

目前对于行人疏散问题的研究主要集中在两方面：进行真人实验和开发行人动力学模型。真人实验取得了一定的成果，但由于其高昂的人力成本和危险性，越来越多的学者转向研究行人动力学模型[1-4]。目前的行人动力学模型包括两类：宏观模型[5-9]和微观模型[10-12]。宏观模型用流量和平均速度来描述行人的整体运动特性，然而却忽略了行人异质性及行人间的相互作用。与宏观模型相比，微观模型侧重于个体之间的相互影响，模型类型更丰富，包括时空连续模型和离散模型。常见的微观模型包括基于牛顿第二定律的社会力模型[13-16]、适用于描述行人排队行为及瓶颈效应的排队论模型[17-18]、用于复杂系统建模的元胞自动机模型[19-21]。

元胞自动机模型是一种广泛用于描述复杂行为特征的网格动力学模型。宋卫国等人[22]利用改进的元胞自动机模型模拟人群的运动，再现了行人的“成拱”和“快即是慢”现象。Varas[23]模拟了基于元胞自动机模型的障碍物对行人疏散行为的影响。Nowak和Schadschneider[24]研究了双向行人流动力学，并提出了一种用于缓解拥堵的预测机制。唐铁桥等人[25]借助元胞自动机模型研究了小学放学时校门口的行人流运动，并发现平均疏散时间与初始分布人数成负相关的关系。Li等人[26]将元胞自动机模型用于模拟行人对垂直步行设施的选择行为。元胞自动机模型具有计算量小、规则简单易行等优势，故而本文取其作为描述行人运动的基础模型。

在疏散过程中，恐慌情绪蔓延可能会导致行人无法快速逃生，且慌乱中极易发生踩踏事故。此时，熟悉周围环境的引导员有序的指引行人疏散，可在一定程度上提高疏散效率及减少人员伤亡。侯蕾等人[27]研究了引导员数量和位置对疏散的影响。李军等人[28]指出引导员可以减小瓶颈拥堵效应，提高出口利用率。Ma等人[29]发现引导员并不总是有助于疏散。Zhang等人[30]提出了一种通过搜索分区网格中的局部最大密度区域来分配引导员的方法。然而上述研究中确定引导员的位置的方法未能综合利用环境及行人分布信息，存在很大的主观性。本文提出一种基于高斯混合模型的引导员分配方案。

高斯混合模型(Gaussian Mixture Model)简称为GMM，是一种广泛应用的聚类算法，由多个高斯分布函数线性组合而成，通常使用期望最大(Expectation Maximization，简称EM)算法进行训练。柴五一[31]提出多分类高斯混合模型和基于邻域信息的高斯混合模型，用于分割图像。欧丰林[32]利用高斯混合模型对目标视频进行建模，融合从卷积神经网络中提取的浅层和深层图像特征的响应值后定位跟踪目标。刘翔宇[33]采用混合高斯模型进行前景划分，以提高行人检测系统的准确率和实时性。高斯混合模型非常适用于复杂对象建模中的多对象划分。本文充分利用高斯混合模型聚类精度高的优势，将其用于确定引导员最优位置及数量，并进一步研究了引导员对行人疏散的影响。

1 模型

1.1 高斯混合模型确定引导员最优数量及位置

高斯混合模型是k个高斯分布函数线性组合。每个高斯分布函数Cw(1≤w≤k)由均值μw和方差σw确定，概率ωw表示各自的权重。对高斯混合模型的求解通常由EM算法实现。贝叶斯指标(BIC)是一种常用的评价聚类效果的方法。利用高斯混合模型，确定引导员最优参数的流程图如图1所示。

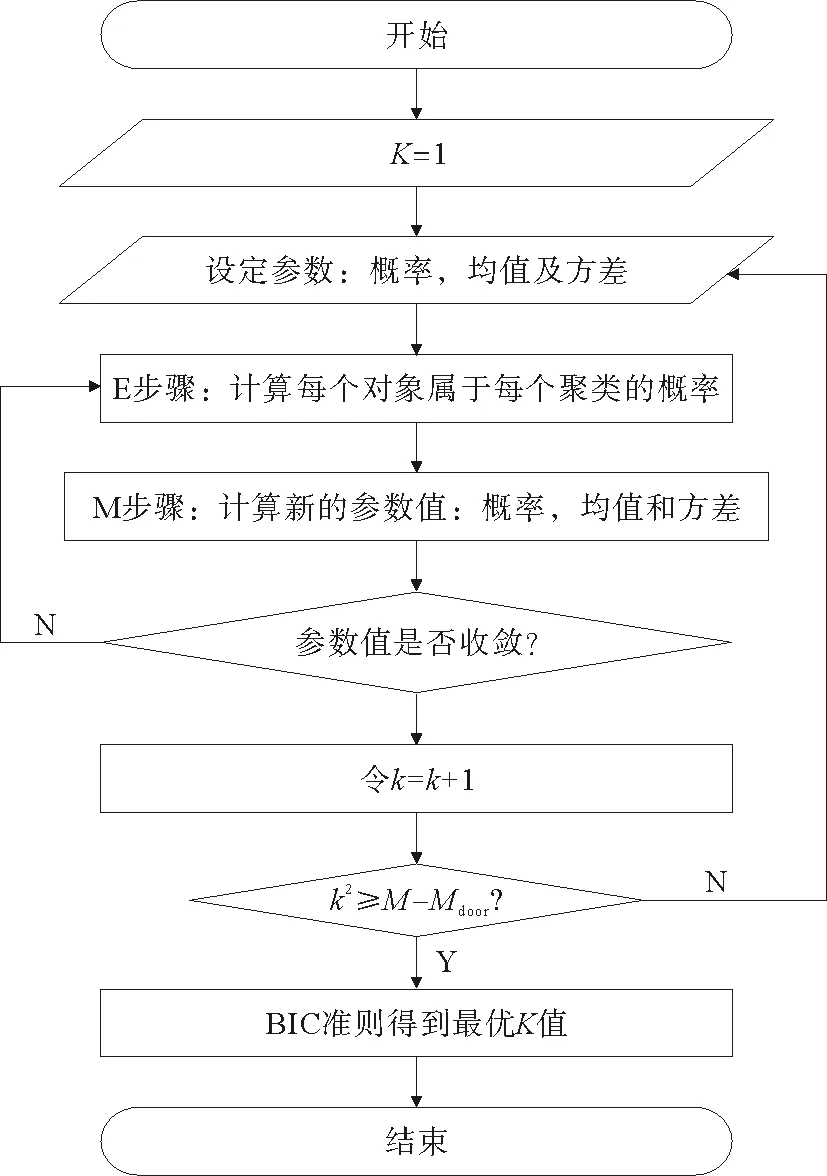
图1 确定引导员最优参数流程图Fig.1 Flow chart for determining the optimal parameters of guides

1)令聚类数k=1。

2)随机设定各聚类的参数：概率ωw，均值μw，方差σw。

3)E步骤：计算每个样本数据xq(1≤q≤n)属于每个聚类Cw(1≤w≤k)的隐变量：概率zq。

(1)

(2)

4)M步骤：重新计算各聚类的参数值。

(3)

(4)

(5)

5) 重复步骤3)和4)，迭代计算直到参数数值收敛。

6) 计算该k值下的BIC

BIC=-2log(L)+klog(n)

(6)

(7)

7) 令k=k+1直到k2≥M-Mdoor，重复步骤2)～6)。

8) 取BIC值最小的情况作为最优聚类。

1.2 基于元胞自动机的行人运动模型

1.2.1 运动优先级

在行人动力学研究中，行人的位置更新策略分为异步更新和同步更新两种。为避免行人位置冲突且考虑到通常是身体素质较高且对环境更加熟悉的行人具有优先移动的事实，本文采取异步更新策略。对每个行人设定随机参数xphy和xfam，其中xphy表征行人的身体状态，xfam表征行人对周围环境的熟悉程度。公式(8)中ypri表征行人的运动优先权，该参数越大表示行人运动优先级越高。

(8)

1.2.2 行人的运动规则

在火灾等突发事件下，行人的视野会受到烟雾的干扰而影响其视域半径Rv。此时，行人的运动可分3种情况进行讨论：1)行人到出口的距离R大于Rv且视野域内存在引导员。此时行人以引导员位置作为目标位置进行移动。2)行人到出口的距离R大于Rv但视野域内不存在引导员。此时行人根据以其所在位置为圆心、2m为半径的圆形区域内其他行人的运动情况来制定移动策略。3)行人到出口的距离R小于Rv时，行人以出口为目标位置。本文假设Rv=4m。

元胞自动机模型有多种类型，本文采用的是如图2所示的摩尔型元胞自动机模型。每个元胞有元胞本身及周围8个邻胞共计9个位置可移动，其运动规则的制定依赖于地板场。地板场分为静态场和动态场。静态场表征的是目标位置的吸引力，行人和引导员的目标位置不同(行人向引导员移动，而引导员需要向出口移动)，因此需要建立不同静态场。动态场表征受其他行人运动路线的影响程度多用于描述从众行为，引导员和行人在同一空间内运动，彼此影响，动态场统一即可。

图2 元胞自动机模型Fig.2 Cellular automata model

i和j分别代表元胞的横纵坐标。设出口元胞的静态场值sij=1，其他元胞的初始静态场值sij=0。如果中心元胞(i0,j0)的静态场值si0j0≠0且其邻胞(i,j)的静态场值sij=0，则sij=sij+1。smax=max(sij)，Sij=smax-sij。遍历每个元胞得到表征出口吸引力的静态场Sij。

设引导员元胞的静态场值s′ij=1，其他元胞的初始静态场值s′ij=0。如果中心元胞(i0,j0)的静态场值s′i0j0≠0且其邻胞(i,j)的静态场值s′i0j0=0，则s′ij=s′ij+1。s′max=max(s′max)，S′ij=s′max-s′ij。遍历每个元胞得到表征引导员吸引力的静态场S′ij。

设置每个元胞(i,j)的动态场值Dij=0。每个时间步长内，每当有行人或引导员经过元胞(i,j)，则Dij(t+1)=Dij(t)+1。同时，如式(9)所示，Dij以α的比例扩散，以β的比例衰减。其中，α=0.2，β=0.05。

Dij(t+1)-Dij(t)=βΔD(t)-αD(t)

(9)

(10)

(11)

当行人(i,j)到出口的距离R小于或等于4 m时，nij=1。当R大于4 m且行人视野域内存在引导员时，nij=0。当元胞空闲时，θij=0；当元胞被行人或引导员占据时，θij=1。其中，KD=0.1，KS=1.8。在下一时刻行人会移动到P值最大的元胞。

1.2.3 引导员的运动规则

引导员掌握着出口位置及周围环境信息并直奔出口，依据已建立的静态场Sij及动态场Dij计算状态转移概率P′来决定下一时刻的目标位置。

(12)

(13)

当元胞空闲时，θij=0；当元胞被行人或引导员占据时，θij=1。其中，KD=0.1，KS=1.8。在下一时刻引导员会移动到P′值最大的元胞。

1.3 行人对引导员的选择

行人运动过程中可能会出现视野域内存在多个引导员的情况，此时行人需要选择最合适的引导员，并跟随其运动。考虑到模糊逻辑方法具有处理不确定性模糊信息的优势，因此本文拟引入模糊逻辑理论来描述行人对引导员的择优判定。模糊逻辑理论是指借助模糊集合和模糊规则模拟人类对事物不确定性的判断，常用于表达过渡性界限或定性知识经验。行人选择引导员时，到引导员的距离及引导员周围其他行人的密度是两个非常重要的因素[34-35]。而距离的“长短”和密度的“大小”都缺乏明确的标准，属于模糊的概念，因此模糊逻辑理论非常适用。

模糊逻辑由5部分组成：变量，模糊化，规则库，模糊推理系统和去模糊化。变量包括输入变量和输出变量。距离(dis)和密度(den)是行人选择引导员时考虑的主要因素，用作输入变量。概率(pro)表征行人对不同引导员的选择概率，作为系统的输出变量。输入变量和输出变量的隶属度函数分别如图3～图5所示。变量间的关系如图6所示。

图3 距离的隶属度函数Fig.3 Membership degree of distance

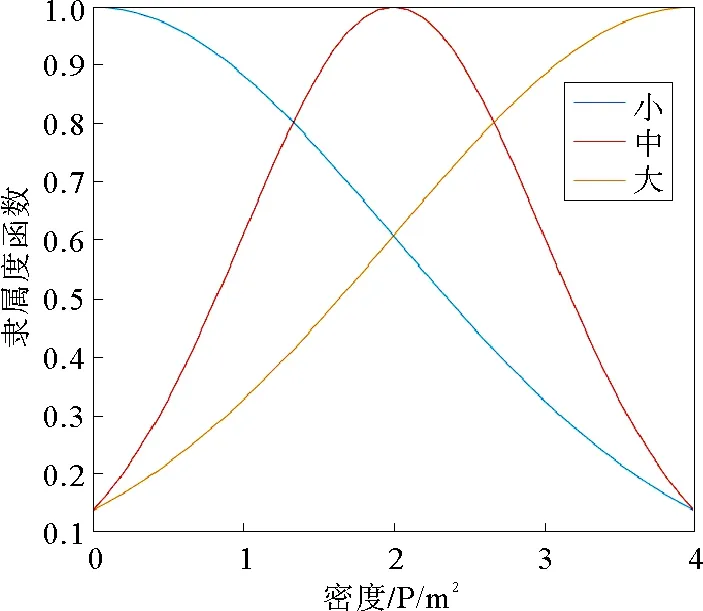
图4 密度的隶属度函数Fig.4 Membership degree of density

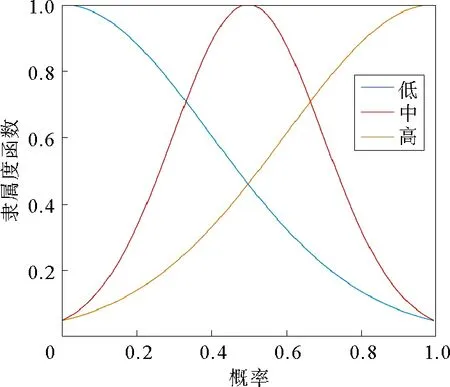
图5 概率的隶属度函数Fig.5 Membership degree of probability

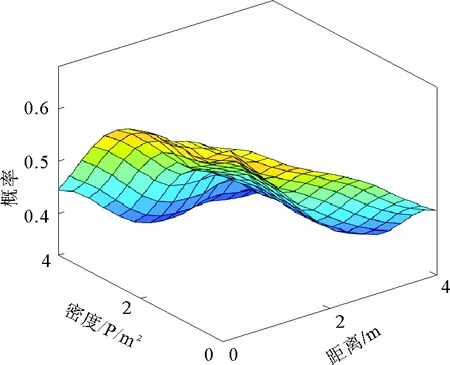
图6 模糊逻辑的变量间的关系Fig.6 Relationship between variables of fuzzy logic

模糊规则是借助自然语言描述变量间的关系，其规则集合如表1所示。

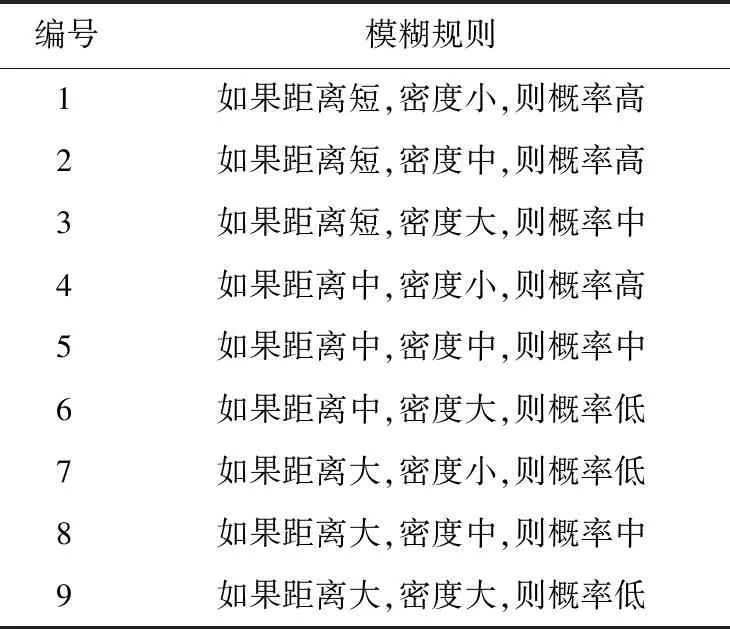
表1 规则库Tab.1 Rule base

在借助模糊规则实现变量间关系的模糊化后，还需解模糊来得到精确值。本文采取如式(14)所示的质心法：

(14)

其中,X是输出变量(pro)的模糊集合，μ(x)为(pro)的隶属度函数。

2 仿真

本文仿真实验是在如图7所示的20m×20m的房间内进行的。出口位于房间上侧墙的中间位置，宽度为1m。我们将房间划分为0.5m×0.5m的正方形元胞，每个元胞或者被占据，或者空闲。行人的运动速度为1.25m/s。仿真部分实验均重复20次以确保数据的有效性。

图7 仿真环境Fig.7 Simulation environment

2.1 行人运动过程

如图8a所示，当T=0s时，由黑色圆点表示的引导员位于最优位置，由其他颜色的圆点表示的行人随机分布在房间内。图8b中，可明显观察到行人向各自视野域内的目标引导员聚集。图8c中，行人跟随引导员向出口移动，距离出口较近的行人开始离开房间。图8d中，引导员带领行人运动到出口附近，出口周围的行人出现“成拱效应”，行人和引导员有序离开房间。

图8 行人疏散过程中不同时刻的快照Fig.8 Snapshots of pedestrian evacuation at different time instants

2.2 引导员数量对疏散时间的影响

由图9可知，房间内无引导员时疏散时间最长。在加入引导员后，行人跟随掌握环境信息的引导员沿最优路径移动，疏散效率得到提升。然而随着引导员数量增加到一定程度(本文仿真环境中，当引导员数量大于4时)，此时继续增加引导员数量反而会导致过多的引导员各自指引较少的行人，疏散效率不再提升，反而增加了人力资源成本。仿真结果数据进一步证明了GMM模型聚类结果的有效性。

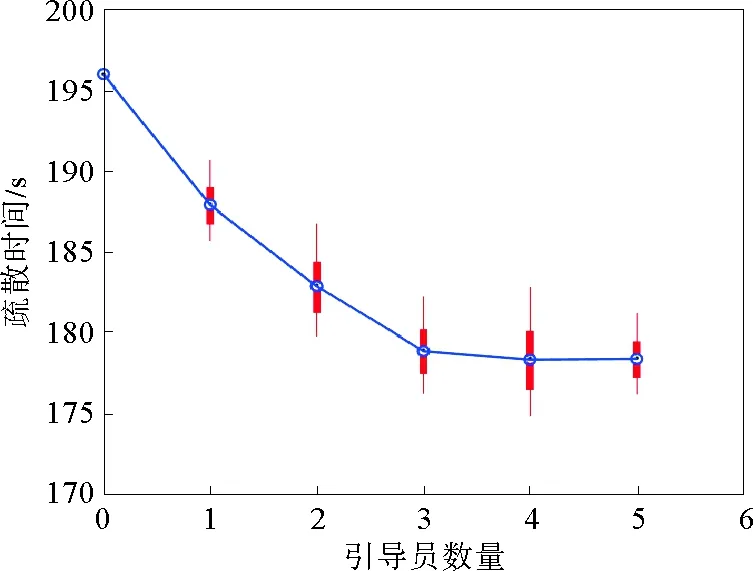
图9 疏散时间与引导员数量的关系Fig.9 Relationship between the evacuation time and the guide quantity

2.3 引导员速度对疏散时间的影响

假设λ为引导员与行人之间的速度比。在图10中，当λ=50%时，一方面，部分行人跟随引导员运动到出口附近，由于行人速度明显高于引导员，行人优先从房间离开，在房间内的引导员继续引导随后的行人，提高了疏散效率。另一方面，引导员速度过慢导致其周围行人密集，反而不利于疏散。当λ=75%时，疏散效率最高。当引导员的速度高于行人即λ>1时，运动一段时间后，引导员会从原本距其较远的行人视野域消失且引导员会较早离开房间，其余行人失去指引，整体疏散效率降低。此外，无论引导员速度快慢，有引导员情况下的疏散时间均低于无引导员场景。进一步说明引导员对行人方向的指引是提高疏散效率的关键。

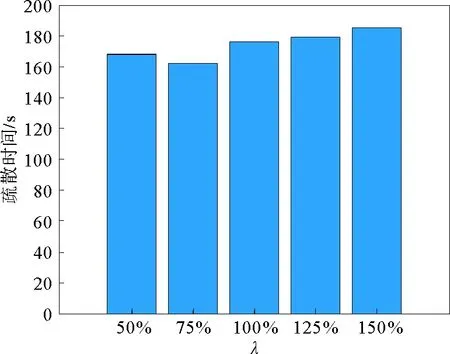
图10 疏散时间与λ的关系Fig.10 Relationship between the evacuation time and λ

2.4 出口宽度对疏散时间的影响

如图11所示，在一定范围内增加出口宽度，出口的通行能力增加，疏散效率提升。增加出口宽度(本文仿真环境中当出口宽度大于3m时)疏散时间基本稳定。这是由于虽然单位时间内允许离开房间的行人数增加了，但是单位时间内到达出口的行人数没变，出口宽度增加但利用率却在下降，所以疏散时间基本不变。出口越宽，其所承受的压强越大，对行人安全有一定威胁。由此可知，结合出口的行人流量规划出口宽度既能保证行人的疏散效率又能减少风险。

图11 疏散时间与出口宽度关系Fig.11 Relationship between the evacuation time and the exit width

3 结论

本文以高斯混合模型确定引导员的最优数量及位置，以元胞自动机模型制定行人及引导员在疏散过程中的运动规则，并利用模糊逻辑方法模拟行人对引导员的选择行为。研究了引导员的数量和速度以及出口宽度3个因素对行人疏散行为的影响，根据仿真结果得到以下结论：一定范围内(本文仿真环境中，引导员数量不超过4，出口宽度不超过3m)，增加引导员数量及出口宽度有利于疏散。引导员的速度不宜过快，当其为行人速度的75%时疏散效率最高。本文提出的模型丰富了对行人疏散问题的研究并提出合理的建议以保障行人快速安全地疏散。但是，周围环境对行人的影响，行人速度异质性等方面仍考虑不周。在未来的研究中，将进一步丰富仿真场景及行人属性。