基于多属性决策的电力网络关键节点识别
何 铭,邹艳丽,梁明月,李志慧,高 正
(广西师范大学电子工程学院,广西 桂林 541004)
0 引言
随着经济的发展和社会的进步,世界各国的电力网络规模及发电量不断增大,大规模电网连锁故障频繁发生,给国家经济和居民生活造成恶劣影响。电力系统作为国家的关键基础设施,电力供应需要高度的稳定性与持续性[1]。近些年的研究发现,电网运行中一些关键环节(发电站、变电站、传输线路)发生故障时,会引起一系列连锁反应导致其他节点相继故障,最终导致大规模级联故障[2-3]。例如2018年3月21日的巴西电网大停电事故以及2015年10月受台风“彩虹”影响广东省湛江出现的大面积停电事故,都是由某个节点损坏引发的连锁故障[4]。因此找到电网中的关键节点或线路并加以针对性的保护,对于预防电网中的大规模级联故障具有重要的实际意义。
由于复杂网络理论的学科交叉特性,使其在各个学科领域得到广泛应用。已有研究表明,电网级联故障的发生与网络拓扑结构紧密相关,于是越来越多的学者将复杂网络理论用于电网关键节点的识别[5-11]。文献[5]运用了网络凝聚度指标评估节点重要度,将删除节点前后的凝聚度变化作为评估依据。文献[6]运用了度中心性、接近中心性等指标构建决策矩阵来对节点评估。文献[7]改进了节点重要度贡献矩阵,更好综合了电网全局特性与局部特性。此外还有基于电气特性的潮流追踪[8]、熵权法[9]、抗灾变性指标[10]法等关键环节识别方法。过去的很多研究是通过单一拓扑或电气指标评价电网节点的重要性,电网是一个超大型的复杂网络,仅应用单一指标评价不够科学,于是有学者提出应用多指标综合评价的方法,文献[11]运用度值和凝聚度等几个指标来综合判断电网节点的重要度,但是文中仅仅考虑了电网的拓扑特性而忽略了真实电网的电气特性,且决策矩阵的权值采用人为主观赋权,不具有客观性。
本文借鉴了先前学者的研究,采用多属性决策的综合逼近理想排序(Technique for Order Preference by Similarity to Ideal Solution,TOPSIS)[12]与灰色关联度[13]相结合的电网节点重要度评估方法,综合了电网节点紧密度中心性指标、凝聚度指标、电气介数中心性指标、PageRank指标与子图指标这5个指标对电网进行评价,决策矩阵的权值结合层次分析法和变异系数法计算得出。该评估模型从多个角度对节点进行综合评价并采用主、客观赋权相结合的赋权方法,避免了单一属性的不足和赋权的主观性,使排序结果更具可靠性。最后选取湖北某地实际电网来验证本文方法的有效性。
1 电网关键节点评估指标
本文将电网抽象成拓扑网络,网络中的节点分两种属性:发电站与变电站/大负载设备。电网不具备能量储存特性,一段时间内发电站提供的能量等于各负载节点消耗的能量。在简化网络时,由于实际负载节点(用户)数量远大于发电站、变电站数目,且消耗功率与发电站的发出功率不处于同一量级,讨论低功率负载节点的关键性不具有任何意义,于是我们将电网中大功率的变电站节点看作负载节点,最终生成简化网络拓扑图。在评估指标的选取中,为了更贴合实际我们采用紧密度中心性指标、凝聚度指标、电气介数中心性指标、PageRank指标与子图指标,把网络的拓扑结构与电气特性结合起来构建关键节点识别指标。定义电气距离为两节点间连边的阻抗之和,最短电气距离为两节点间阻抗值之和最小的线路。
1)紧密度中心性指标[14]
中心性反映的是网络中各节点的相对重要性,紧密度中心性则反映了节点在网络中居于中心的程度,其表达式为:
(1)
其中,N为网络节点数,dij为节点Vi到节点Vj的最短距离。若C值越大说明该节点的位置越处于网络中心,在网络中的重要度就越高。
2)凝聚度指标[15]
网络的凝聚度定义为节点数N与平均距离L乘积的倒数:
(2)
其中,L为网络的平均最短电气距离。节点凝聚度指标是用节点收缩后,网络凝聚度的变化量来衡量节点的重要程度:
(3)
其中,CC和CC*表示节点i收缩前和收缩后的网络凝聚度。D(Vi)的数值越大说明网络凝聚度值变化越大,节点就越重要。
3)电气介数中心性指标
将介数[16]与电力网络电气特性相结合,因为电能传输的损耗与线路阻抗有关,这里计算线路介数时考虑电网的线路特性。定义电气介数为电网中两个不相邻的节点间的最短电气距离经过某节点的次数,经归一化处理得到电气介数中心性。电力网络传输中经过某一节点的次数越多表示该点在网络中的位置越重要。表达式为:
(4)
其中,Bi表示两个不相邻的节点间最短电气距离经过点vi的次数。该指标的数值越大说明节点在电网传输中起到的作用就越大,节点就越重要。
4)PageRank指标
PageRank[17]是按照每个节点对其他节点的贡献程度大小的排序,通过状态转移概率矩阵不断迭代计算出最后结果。该定义用于计算有向网络的节点重要度。我们根据电网潮流方向将网络变为有向网络。定义网络邻接矩阵B=(bij)N×N,记矩阵B的各行各列为
(5)
其中,cj表示节点的链入数,ri表示节点的链出数,其状态转移规律用Markov链来表示,构造转移概率矩阵A=(aij)N×N,其中:
(6)
其中,aij即从点i转移到点j的概率,d为模型参数,通常取值d=0.85,求出满足式(7)的Markov链的平稳分布x:
(7)
表示在极限状态(无限次转移)下每个节点被访问的概率分布,由此排列出节点重要度大小。
5)子图指标[18]
节点的度是网络最基本的特性之一,表示网络中与该节点直接相连的节点数量,但是单单考虑节点的连接性是不可靠的,因此引用子图这一指标,不仅延续了节点之间的关联特性,还将连接扩展到一定范围,在计算过程中考虑到了二次和二次以上的连接,综合节点的深度连接关系反映节点的重要性。表达式为
(8)
其中,μn(vi)=(B)nii,(B)nii为邻接矩阵B的n次幂的第i个对角线元素,μn(vi)为以节点vi为起点经过n个连边回到节点vi的回路数目。
2 评估模型
本文基于TOPSIS法综合了5种评价指标来对电网节点重要性进行评估。TOPSIS法的核心思想是求出各指标的正负理想解,并以此为基准计算出指标与正负理想解的贴近度来对节点进行排序。计算过程中的比对需要用到所有的原始数据,因此对原始数据的利用率充分,适用于电网模型。虽然该方法基于评价数据本身,但是在评价大型复杂网络如电网、交通网、航空网等时,这些信息数据对于整个复杂网络规模来说依然是“小样本”、“贫信息”的,于是我们引入了灰色系统理论[19-20]中的灰色关联度这一指标,用于处理该类小信息量的系统数据,作为很好的补充。于是我们采用TOPSIS方法,结合灰色关联度与主客观赋权法得到指标的权值,实现电网中节点重要度的多属性决策排序。
在评估电网重要度时,将电网中的节点数计为N,评价指标的个数为M。构成评价矩阵X,有:
(9)
其中,Xim表示第m个指标对应节点i的评价结果。决策流程如下:
第1步:将电网的决策矩阵标准化得到标准化评价矩阵Y,有:
Y=[yim]N×M
(10)
第2步:对标准化评价矩阵Y赋权值生成加权评价矩阵Z,有:
Z=[Zim]N×M
(11)

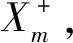
(12)
正理想解为在同一指标中得出的评价结果最大的数,负理想解为在同一指标中得出的评价结果最小的数。
第4步:计算各评价方案与正、负理想解的欧式距离
(13)

(14)
其中,ε(0,1)为分辨系数,通常取ε=0.5,得到正负理想的灰色关联度为
(15)

(16)
其中,α与β反映的是偏好程度,满足α+β=1,α,β反映了节点i综合各指标的评价结果与正理想方案的接近程度,其值越大越优;反映了节点i综合各指标的评价结果与负理想方案的接近程度,其值越大越劣。这里将欧式距离与灰色关联度看为同等重要,系数α与β均取0.5,计算出贴近距离。
第7步:计算出相对贴进度:
(17)
根据贴进度的大小对节点重要性从大到小进行排序,得到电网关键节点的最终评估结果。
3 权重设置
第2节中参数权重ω的选取对于多属性评估方法的结果影响很大,为了使结果不完全依赖于人的主观判断,本文采用了主客观组合赋权法[21-23]同时兼顾了主、客观的权重。主、客观赋权分别采用层次分析法和变异系数法,然后综合两者计算结果得到最终的组合权值。
3.1 基于主观层次分析法的主观权重
层次分析法常用于多属性决策的主观赋权中,其基本的原理是考虑决策对象之间的相互关系来分层,构建多层次模型来计算各指标的重要程度。方法具体流程为:根据各指标的定义并结合前人的研究经验将需要评估的m个指标进行人为主观的赋值,赋值区间为1到7之间的整数,指标的赋值定义为Ha,a∈[1,2,…,m],然后将所有指标的H值进行差值比较,生成标度矩阵R=[rij]m×m。当指标i与指标j比较时,若Hi>Hj,rij的值由表1给出;若Hi 表1 对比标度定义Tab.1 Definition of contrast scale 根据以上约束得到标度矩阵R: (18) 采取两种方式求出权重,首先根据式(18)将标度矩阵R每一列进行归一化处理,得到判别矩阵G=[gij]m×m,其中gij: (19) 后将判别矩阵G每一行取算术平均得到第一个权重矩阵H=[hi]m×1: (20) 然后将判别矩阵G通过式(21)计算得到另一个权重矩阵K=[ki]m×1: (21) 将式子(20)与(21)的权重矩阵相应元素几何平均得到最终主观权重矩阵ξm。 变异系数法(Coefficient of variation method)是直接利用各项指标所包含的信息,通过计算得到指标的权重,是一种客观赋权的方法。其基本原理为:指标取值差异性越大,该指标包含的信息量越多,所占的权重越大。该方法会利用决策矩阵中的所有数据。计算公式如下: (22) (23) 综合主、客观的权值结果计算出最终的组合权重ωm: (24) 综上是整个关键节点识别流程,包括评估模型与权重设置两部分,程序均在Matlab编程运行。接下来从时间维度分析算法的复杂度,评估模型部分包括评价矩阵计算和模型计算,评价矩阵由各评价指标计算而来,各指标算法的复杂度为O(N^2),N为网络节点数;模型计算中结合灰色关联度的TOPSIS算法的复杂度为O(N×M) ,M为评价指标个数。权重设置部分由层次分析法与变异系数法结合得来,该部分杂度为O(M^2)。综合分析整个算法的时间复杂度为O(M×N^2+N×M+M^2)。在处理器为Intel Core i5-7300HQ下运行下例IEEE30节点中程序运行总时间为1.618 1s。电网关键节点识别的流程图如图1所示。 图1 算法流程图Fig.1 Algorithm flowchart 本节以IEEE30节点网络为例在其基础上进行仿真实验,该系统拥有6个发电机节点和24个负荷节点。系统拓扑结构如图2所示。 图2 IEEE30系统拓扑图Fig.2 Topology of IEEE30 System 我们根据流程图先得到决策矩阵,在计算权重时我们结合各指标的特性做出主观赋值。根据各指标的定义并结合前人的研究经验,凝聚度指标为局部指标,所以认定为重要性最差赋值为1;子图指标为度的扩展,是局部指标,但是涉及到了与该节点连接的二级及以上节点给该指标赋值为3;紧密度中心性指标和PageRank指标既考虑局部也考虑了全局指标,但PageRank指标同时考虑了各个节点间的相关性可信度较高,分别赋值4和6;电气介数中心性指标是全局指标同时考虑了电气特性,赋值为5,根据3.1节表1通过各指标的赋值差,得到指标的标度值矩阵,并通过一致性校验,得到标度矩阵R: 计算得到主观权重为:ξ1=0.183 8,ξ2=0.099 0,ξ3=0.239 0,ξ4=0.332 3,ξ5=0.145 8。 客观权值由标准化评价矩阵而来,计算得到:η1=0.111,η2=0.197 4,η3=0.315 9,η4=0.182 8,η5=0.192 7,综合两者得到组合权重依次为:ω1=0.100 0,ω2=0.095 6,ω3=0.369 5,ω4=0.297 4,ω5=0.137 5。根据各指标的权值,我们利用Matlab编程计算出网络所有节点各个指标的重要度值排序,排序结果见表2,这里仅列出排序较高的前10个节点,评估指标的重要度值均为标准化后的结果。 表2 IEEE30系统节点重要度排序Tab.2 Importance ranking of IEEE30 system nodes 从表中的排序结果可以看出来,这几个指标与综合评估的排序都不尽相同,这些指标是从不同的角度对节点的重要信息进行反映,但每个单一指标存在局限性。依据紧密度中心性指标、PageRank指标排名前10的重要节点中有8个位于综合评估指标排名前10的节点中;依据凝聚度指标、电气介数指标、子图指标排名前10的重要节点中有9个位于综合评估指标排名前10的节点中。但各单一指标计算出的节点重要度顺序与综合指标不同,综合评估法将多个指标相结合,弥补各指标的不足,提高了评价的可靠性。 为了进一步说明本文评价方法的合理性,我们选取重要度排序最大的10个节点与其他不同文献中方法作对比,结果如表2所示。各方案的侧重点有所不同:方法1侧重电网运行电压可靠性[24]、方法2侧重电网运行中的能量值[25]、方法3侧重电网受扰后的抗扰及网络传导能力[26],因此在重要度的排序中有些差异,但在重要节点识别上可以看出本文识别方法中排名前10的节点,与方法1和方法3排名前十的节点有7个相同,与方法2中有5个相同。本文排名前三的节点6、10、12三个节点在各对比方法排名前十的节点中都有出现,而方法1-3中排名前三的节点都没有在其他两种方法前十重要节点中同时出现。这进一步说明本文重要节点识别结果的合理性。 表3 节点脆弱度结果对比Tab.3 Comparison of node vulnerability 为了验证电网中关键节点识别结果的合理性,下面利用网络效能和网络临界同步耦合强度两个指标,从拓扑结构和动力学性能两个方面来验证本文所提方法的正确性。 在复杂网络中,网络效能用于描述网络的传输效率。在电力系统中,当一个电力网络遭到破坏时,首要关注的是最终电网的传输效率,我们将移除重要节点前后的网络完整度做对比,得到电网的网络效能,定义如下: (25) 式中N为节点数,dij表示网络中节点vi到vj的最短电气距离,对比按照不同方法移除节点后剩下网络的网络效能值,剩余的网络效能越小说明被破坏节点对网络的完整性越重要,结果如图3所示。 从图3的仿真结果可以看出,采用本文方法识别出的关键节点被移除时,对电力网络的整体破坏力度要更大,网络效能下降速度更快。在依次移除4个节点后,电网效率下降到原网络的百分之三十以下,说明了本文关键节点识别方法的正确性。 图3 网络效能指标对比Fig.3 Comparison of Network Efficiency 接下来从电力网络的动力学角度,利用临界同步耦合强度指标进行验证,我们采用二阶类Kuramoto相振子模型[27]作为节点动力学模型来分析电网的同步能力,模型定义为 (26) 图4 临界耦合强度指标对比Fig.4 Critical Coupling Strength Comparison 从图4的不同方法对比结果可以看出,系统的稳态序参数随着振子间耦合强度的增大而增大且趋于1。图中每次节点移除后,各方法的剩余子网同步临界耦合强度大小依次为Kc(图a)≥Kc(图b)>Kc(图d)>Kc(图c),临界同步耦合强度Kc越大,表示剩余系统的同步能力越差,意味着移除的节点在网络中的重要性越高。按照本文方法将排序前三的节点移除后,剩余系统同步临界耦合强度达到了79,系统基本上很难同步,而其他系统均在25以下,因此本文方法识别的关键节点对维持系统的同步运行更重要。 接下来将本文提出的关键节点识别方法应用到湖北某地实际电网上进行仿真分析。由于电能的特性,一段时间内发电量等于负载设备消耗的电量,我们忽略小功率负载对电网的影响,将该地区电网中550kV的换流站作为发电机节点,220kV以上的变电站提取出来作为负载节点得到简化的拓扑图如图5所示,其中区域电网共包含4个发电机节点,24个负载节点,45条输电线路。图中1,2,3,4号节点代表发电机节点,其余节点为负载节点。 图5 湖北某地实际电网拓扑结构简化图Fig.5 Simplified diagram of the actual power grid topology in a certain area of Hubei Province 从拓扑图中可以看出该地区的发电机比较靠近中部,负载分散在四周。网络度分布近似幂率分布,说明该网络具有BA无标度网络特性。3号发电机周围连接的负载节点较多,与1号和4号发电机相连,3个节点组成了区域电网的核心,占据了关键位置且是重要的发电组成,主观分析可知这3个节点对于网络的供能和能量的传输起重要作用。 网络节点的权重由网络标准化评价矩阵使用主、客观法从5个指标值的对比中获得,计算得到各指标的综合权重分别为ω1=0.060 8,ω2=0.101 3,ω3=0.383 9,ω4=0.204 2,ω5=0.249 9,可知电气介数中心性指标和子图指标在该网络所占权重相对较大,与IEEE30系统得到的权重相比,后者的电气介数指标与PageRank指标权重占比相对较大,由于两者网络拓扑结构不同,计算出的各指标权重占比不同,这样将权值的设置很好地结合了不同网络的结构特性而不是将所有网络权重固定。 运用本文方法计算出节点重要度值排序结果见表4和图6所示。排在前4的节点分别是3、1、2、4号,且3号节点在5项指标中有4项都是排第一位,另一项指标虽排第二但是与排序第一的节点重要度值十分接近,综合评估知该节点在网络是最重要的节点,1号和2号在四项指标中占据了前三位,通过电气介数这一指标中可得前三号节点在网络传输的重要性比往后排序的节点要高出许多,说明了这些节点传输的关键性。我们从实际数据中得知按变电站传输线路的电压排序是3、1、4、2号,虽然2号节点排序在1号节点后,但是2号节点在网络中是作为枢纽输送给外省,结合实际分析2号节点的重要度在4号之前是可行的。假若电力网络中发生了级联故障,首要保护好这些节点能使电网整体功率不会陡降,减少网络损失负荷,能避免造成更大规模的停电事故。对比结合拓扑图和电气特性的主观分析和本文模型的计算结果看出,两者对电网关键节点的识别基本一致,进一步验证了本文方法的可行性。 表4 节点重要度排名前10的节点排序Tab.4 Ranking of top 10 importance nodes 本文基于TOPSIS法提出了一种新的电网关键节点识别方法。该方法综合考虑了电网的紧密度中心性、凝聚度、电气介数中心性、PageRank、子图5个指标,将多属性决策与主客观组合赋权法相结合来综合评估电网节点的重要性。针对当前类似研究中所采用的指标单一、未考虑电气特性和选取权重太过主观或者客观这些不足,将传统指标结合了电气距离参数进行改进,从多个评估角度对网络进行分析,结合主客观组合赋权法,使本文方法对电网关键节点的识别更加全面。随后,我们从网络结构和动力学两方面与其他识别方法进行比较,实验结果表明本文方法优于其他三种识别方法,最后结合实际电网进行验证,评估结果同样说明了本方法的有效性。
3.2 基于变异系数法的客观权重


4 算例分析
4.1 IEEE30节点系统仿真



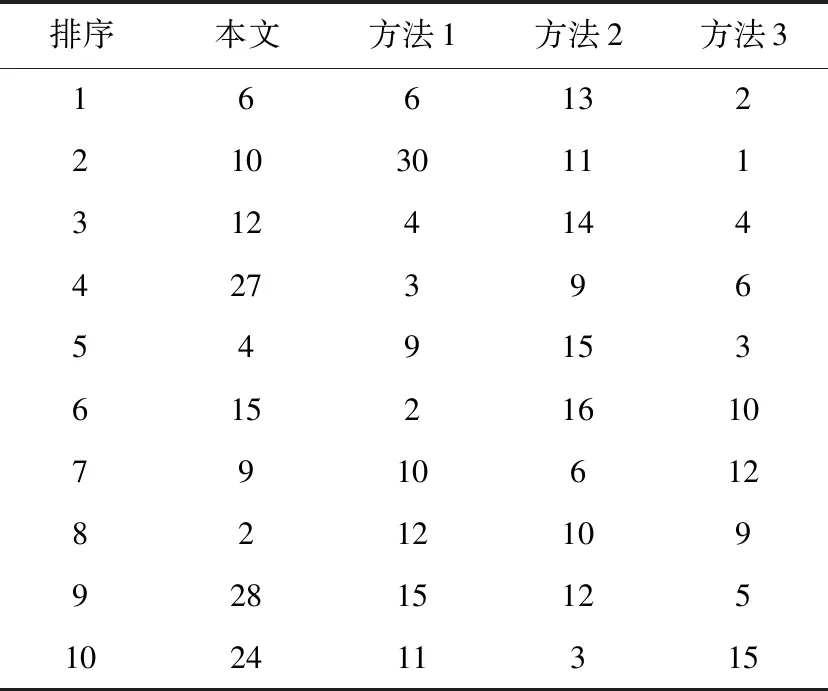
4.2 不同指标识别结果对比验证



4.3 湖北某地实际电网仿真


5 结论

