干式变压器有限元仿真模型的电磁和振动分析

陆 昕 周 雄 钱帅伟 潘 笑

(1 广西电网有限责任公司桂林供电局 桂林 541000)

(2 武汉大学电气与自动化学院 武汉 430072)

0 引言

干式变压器因具有损耗低、体积小、维护简单等优点而被广泛应用于室内供配电场所。由于电力需求的增长，干式变压器的数量也在不断增加。运行的干式变压器存在振动以及噪声的问题，给附近的居民和环境带来干扰。

绕组铁芯振动是造成干式变压器噪声的重要原因[1−6]。其中铁芯振动和噪声的两个主要来源为：(1)交变磁场中硅钢片的非线性特性会引起磁致伸缩[7]；(2)铁芯并不是一个整体，在硅钢片叠片之间存在缝隙，这种缝隙处的漏磁也能够在存在电流激励的情况下对导体产生电磁力，从而引起振动[8−9]。

当变压器绕组中通入交变电流时，绕组的周围会产生磁场，除去沿着铁芯闭合的主磁通，还有漏磁通，从而产生了漏磁场。在此漏磁场中的绕组之间以及导线之间会受到电场力的作用而产生振动。绕组振动是造成变压器带载运行振动的主要来源[10]。

由于上述问题的存在，众多研究人员围绕干式变压器的电磁力和振动展开了大量研究。文献[2]进行快速傅里叶变换(Fast Fourier transform,FFT)分析和频域振动分析，得到变压器铁芯和绕组表面各点的振动位移；文献[11]对变压器进行了声强和振动测试，并对其频率特性进行了详细分析；文献[12]在耦合场理论的基础上完成了变压器在运行时由电动激励到绕组振动响应的整个过程的仿真分析，建立了包括各向异性磁阻张量和磁阻质在内的电力变压器铁芯磁-机械强耦合模型；文献[13]建立了基于电-磁-结构力学多物理场耦合的变压器铁芯和绕组综合振动的三维模型,并通过仿真和试验进行对比验证，得到了直流偏磁对变压器振动的影响。但现有研究大都对干式变压器的铁芯和绕组进行分析，因为变压器不同部位具有不同的振动特性，而且不同部件的振动之间是互相影响的，因此在振动特征频率下，对干式变压器整体进行分析对变压器的减振降噪具有重要意义。

基于以上研究，本文构建了变压器本体振动的有限元模型，进行了电磁分析，得到相应的磁场分布。在此基础上，利用结构动力学对变压器模型进行模态分析以及谐响应分析，并且进一步对其在特征频率下的振动云图进行比较分析。

1 干式变压器本体建模

现场安装的SCB10-800KVA 10/0.4干式变压器如图1所示。本文针对这种常见的干式变压器进行分析，建立了有限元实体模型。因为干式变压器中零部件多且连接方式多样，很难对其进行精确的有限元网格划分以及有限元计算。因此，整体建模不是精确到所有零件的建模，而是从主要方面分析建模，所以需要简化处理干式变压器。

图1 SCB10-800KVA 10/0.4干式配电变压器Fig.1 SCB10-800KVA 10/0.4 dry-type distribution transformer

基于以上分析，本文在对变压器进行建模分析时进行了如下简化：

(1)在建立模型时，不仅需要保持水平截面外缘轮廓形状，还要保证铁心中心柱、铁轭、中心柱的长、宽、高、直径等各种尺寸与图纸完全一致，将旁柱以及立柱简化，使其成为一个整体形式。

(2)由于夹具的结构比较复杂，在简化的仿真模型中，将仅考虑铁芯叠硅钢片的结构。

(3)将绕组线圈视为一个整体处理。将变压器绕组等效为圆筒形状，保持内外半径、圆筒的高度与实际测量的尺寸一致。

图2 变压器油箱简化模型视图Fig.2 Simplified model view of transformer tank

(4)将冷却风机等效为一个块状的固体，并与下方的固定支架进行合并。

根据实际变压器的模型，在Solidworks中绘制出简化后的油箱仿真模型如图2所示。

2 干式变压器仿真电磁分析

在进行ANSYS Workbench 电磁场分析时，若要计算电磁场的瞬态仿真，可以利用集成在其中的Maxwell 3D模块。本文根据瞬态磁场模块模拟干式变压器绕组和铁芯的磁场分布。在对干式变压器进行电磁场仿真时，考虑其处于空载状态时的仿真结果。

当变压器处于空载时，将高压侧绕组电压给定为11268 kV，三相的输入电压如图3所示。

由图3可以发现，在0.06 s时已经接近稳态，下面观察t=0.08 s时的磁场分布，如图4所示，其中图4(a)为此时刻对应的铁芯和线圈表面的磁感应强度分布云图，图4(b)为此时刻周围空间的磁感应强度矢量分布云图。

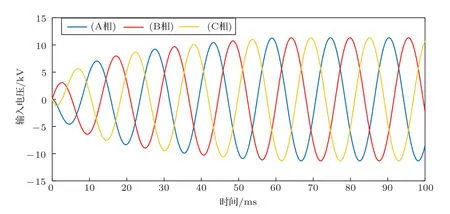
图3 三相空载输入电压Fig.3 Three-phase no-load input voltage

图4 t=0.08 s时的磁场分布Fig.4 Magnetic field distribution at t=0.08 s

从图4中不难看出，最大磁通密度主要分布在铁芯上，仿真过程中变压器处于空载状态，实际上负载的情况也类似。这里计算其磁通分布，可以通过公式(1)求解绕组中产生的轴向电磁力，但是这个公式的计算并不精确，只能大概地表明其磁场分布与电磁力是正相关的[14]。

铁芯磁致伸缩及绕组受到的周期性电磁力作用时所产生的振动，是造成变压器产生振动和噪声的根本原因。因此若对变压器的振动特性进行准确的仿真，则还需要响应可靠的激励值。目前对于变压器内部电磁力计算的理论还不能给出完全精确的计算结果。因此，为了使问题简化，在输入给定激励的条件下，以数值模拟的方法来计算相对振动的幅值。

3 干式变压器仿真振动分析

3.1 模态分析

模态分析是以响应频谱分析为基础的计算结构振动特性的数值技术，结构振动特性包括振型以及固有频率[15]。针对本文中对应的变压器本体模型，求取的前100阶模态的固有频率，如图5所示。

图5 变压器本体前100阶固有频率Fig.5 The first 100 natural frequencies of the transformer body

图6 干式变压器本体前6阶模态典型图Fig.6 Typical diagram of the first 6 modes of the dry-type transformer body

物体实际的振动是各阶振动的结合，但是高阶振动相对来说影响较小，因此主要考察前6阶的振动特性即可。从图5中也不难发现，频率在1000 Hz以内时是振动集中的主要位置。前6阶模态对应的云图中典型部分如图6所示。

在图6中，干式变压器的每种模态代表的是变压器的振动形式。从图6可以看出，铁芯顶部及夹件与绕组的振动相对于干式变压器本体的其他位置来说更为强烈，所以在考虑本体的谐响应分析时，只需主要考察铁芯、绕组线圈、变压器上端夹件等几个位置的振动情况。

3.2 谐响应分析

由于干式变压器的结构比油浸式变压器简单，若不考虑底部风机的振动，变压器的噪声则主要由铁芯和绕组线圈的振动引起。在进行谐响应分析时，将等效的振动力施加在铁芯和线圈的上沿，根据实测值输入，再考察线圈位置、风扇位置、铁芯顶部、上端排线、左侧铁芯的响应，进行对照。显然，各个单元之间的响应特性并不完全一致，此时只要比较最大的振动幅值即可。输入的数据可以根据实际测量的结果得到，如图7所示。

图7 实际测量中3种情况下变压器铁芯上端夹件的振动曲线Fig.7 The vibration curves of the upper end clamps of transformer core measured in three cases

虽然在不同的工作状况下，变压器振动的情况会有所不同，但对于仿真分析而言，更多的是要考虑极限情况下，即当变压器本体振动最严重时，变压器的振动如何传播。在图7给出的实际测量振动值中，空载情况下的振动最为严重，而且含有较高的谐波成分，在800 Hz左右仍然含有谐波成分。考虑到大于1000 Hz时，谐波成分基本不存在，因此大于1000 Hz 部分在本文中将不予分析。利用第2节所建立的干式变压器模型进行仿真，研究空载情况下1000 Hz以内的谐响应分析，以10 Hz为步长，获得较精确的响应曲线，如图8所示。

由图8不难看出，在0∼1000 Hz的范围内，干式变压器不同位置的响应曲线会有很大的不同。线圈、铁芯以及上端排线位置的振动较为明显，下端风机位及固定导轨的振动则相对较小。

图9为实测线圈侧边与铁芯顶部的振动曲线。将图9(a)与图8(e)、图9(b)与图8(c)进行比较，可以发现仿真结果与实测值相差不大。本文在有限元仿真对变压器进行了大量简化，此结果验证了本文所搭建模型、简化方法与仿真方法的正确性。

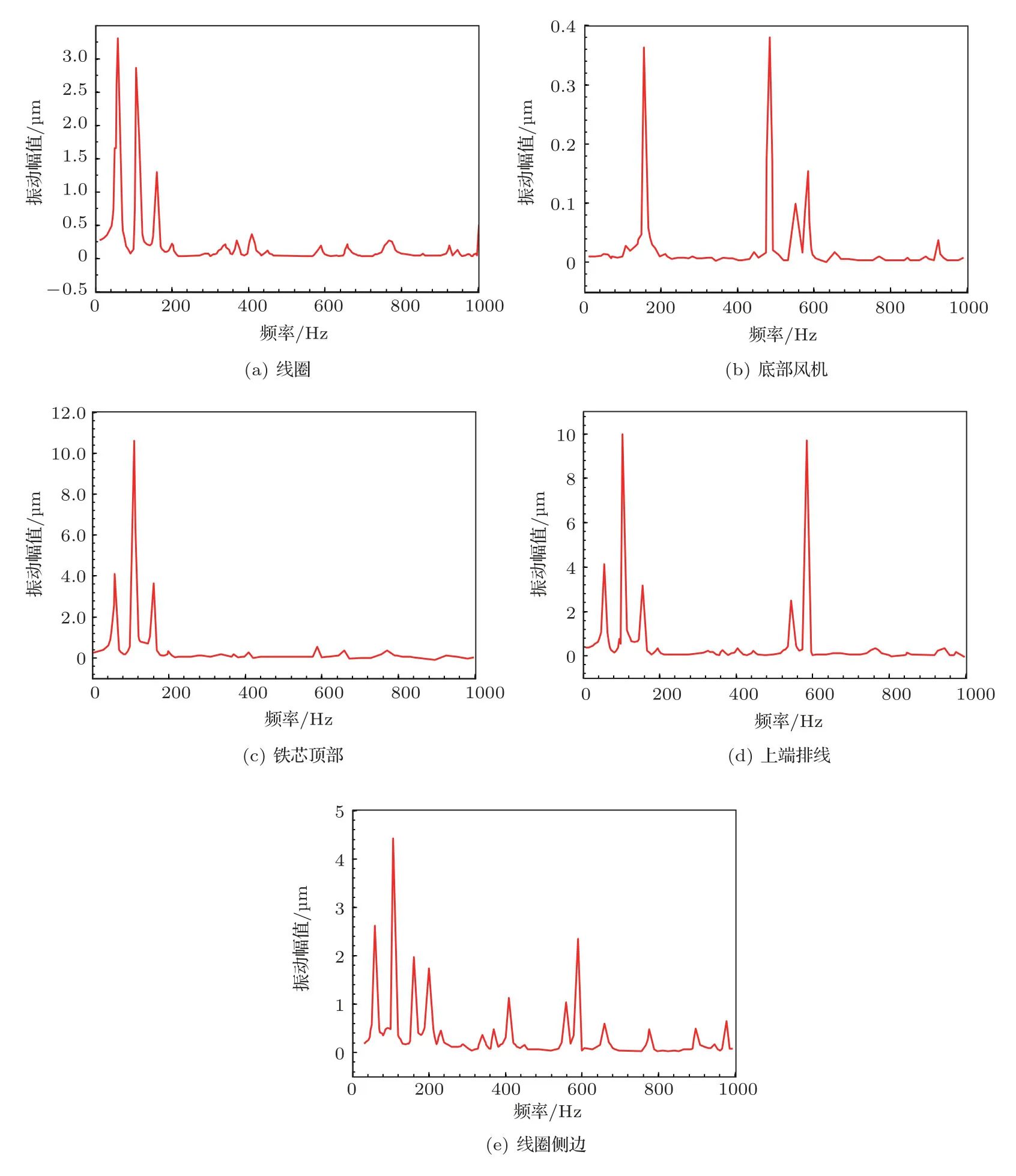
图8 谐响应分析对应的各点频率-位移曲线Fig.8 Frequency-displacement curve of each point corresponding to harmonic response analysis

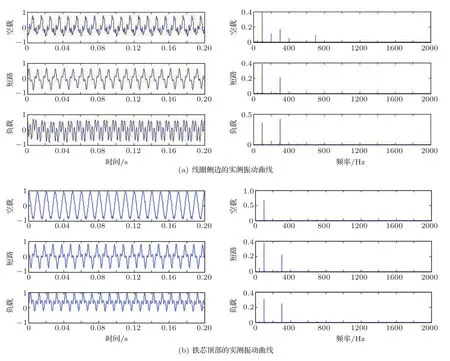
图9 实测振动曲线Fig.9 Measured vibration curve

3.3 振动云图分析

本节将考察谐响应分析的振动云图，这与模态分析有相似之处，但又有所不同。模态分析给出的是振动强度的分布，谐响应分析是给定了输入量，求解具体的振动位移分布规律。

本文现场测量了桂林某个小区的配电室，现场测试如图10所示。

图10 现场测试图Fig.10 Picture of field test

如图10所示，该变压器处于正常运行状态，本文通过测振仪对其防护罩表面的振动进行测量，可以得到变压器总体的振动速度以及加速度的波形图。对所测数据进行频域分析，可以得到如图11所示的频谱图。

图11 变压器振动频谱图Fig.11 Spectrum diagram of transformer vibration

图12 谐响应分析对应的应变云图Fig.12 The strain contours corresponding to harmonic response analysis

从图11中可以看出，变压器的振动主要集中在10 Hz附近以及工频倍频处，因为工频交流电源的频率是50 Hz，变压器振动存在着与工频50 Hz呈倍数的特征频率，其在特征频率处对应的速度与加速度幅值较高。因此在振动云图的分析中，只需要考虑特征频率处的振动规律即可，图12给出仿真中前5次谐波的分布规律。

从图12中可以看出，大部分情况下，干式变压器箱体的振动主要集中在上部排线和线圈部分，为了更加直观得到振动的传递规律，本文在变压器表面选取多个测点进行分析，其中测点1∼3分别为变压器中部从上到下依次选取的测点。在不同特征频率下，对测点的振动幅值进行测量，可以得到图13。由图13可以看出，振动的传递从上往下是一个依次减弱的关系。

在高次谐波下谐响应应变云图中，发现在某些频率下振幅也比较大，如图14所示。

图13 特征频率下各测点的振动幅值Fig.13 Vibration amplitude of each measuring point under characteristic frequency

图14 高次谐波下的谐响应应变云图Fig.14 The strain contours corresponding to harmonic response analysis of higher harmonic

当然，像图14这样的仿真结果可能与实际有出入，因为现实中在任何情况下都是变压器作为一个整体进行振动，而不是变压器的某个边缘单元独自振动。但是在750 Hz 情况下的振动强度明显高于250 Hz以内的部分频率下的振动强度。而小于250 Hz是变压器绕组与铁芯振动的主要频段[1,10]。这表明，变压器整体作为一个系统，除了受到外界的受迫振动之外，其振动特性还会与自身的结构属性有关。

4 结论

本文依据干式变压器本体振动和噪声的产生机理，对干式变压器的振动本体进行有限元模型的搭建与仿真，可以得到以下结论：

(1)利用结构动力学分析变压器本体振动的有关规律，对比模态分析和谐响应分析的振动云图，可以发现振动的传递从上往下是一个依次减弱的关系，变压器的线圈、铁芯以及上端排线位置的振动较为明显，下端风机位及固定导轨的振动相对较小。

(2)通过对干式变压器振动数据分析，发现变压器的振动存有特征频率。由频域图可以看出，振动信号的频率主要集中在400 Hz以内，400 Hz之外的频率处振动幅值几乎为零。变压器的振动主要集中在10 Hz处，50 Hz、100 Hz、150 Hz 等工频倍频处也有分布。非工频倍频处谐波的振动幅值远小于10 Hz处的振动幅值。因此研究干式变压器的减振降噪时可以根据以上规律进行研究。