调节水床效应的双梯度有源噪声控制自适应算法∗

吴礼福 陈晶晶 郭业才

(1 南京信息工程大学 电子与信息工程学院 南京 210044)

(2 江苏省大气环境与装备技术协同创新中心 南京 210044)

0 引言

相对于无源降噪方式，有源噪声控制(Active noise control,ANC)[1−2]在控制低频噪声方面具有明显的优势，因而被广泛应用于各种降噪领域。有源噪声控制系统分为前馈和反馈两种结构：前馈系统需要参考信号，系统降噪量高、稳定性好；反馈控制系统结构简单，但是稳定性差，存在水床效应[3−7]。

水床效应是指一个频段内的噪声减小必然导致另一个频段内的噪声放大[8]。文献[9]采用最小二乘滤波器离线设计方法对水床效应中的噪声放大进行展平以调节水床效应，该方法不具有自适应能力。文献[10]采用小波包分解噪声信号调整反馈控制系统的控制器以达到自适应能力，但是未考虑水床效应中的噪声放大问题。目前调节反馈系统水床效应的自适应算法主要是通过限制控制器系数的大小，直接或者间接地限制次级信号的大小来实现的，例如时域泄漏(“Leaky”)算法[11]，Qiu 等[12]提出的重缩放(“Rescaling”)算法，这些算法能够改善系统的稳定性但没有明确考虑水床效应中的噪声放大问题。Wu等[13]提出将泄漏算法中的泄漏因子替换为泄漏矩阵来调节噪声放大，由于每次迭代都有矩阵和矢量的乘运算，其计算复杂度给实际应用带来困难。Wu 等[3]又提出在频域以控制某个频段内的幅度响应小于指定阈值为约束条件，对指定频段内的噪声放大量进行调节，但是没有直接对次级信号进行约束。

为了综合考虑水床效应的噪声放大和计算复杂度问题，本文提出一种调节水床效应的双梯度有源噪声控制自适应算法，它直接约束次级信号在一定范围内，从而达到有效调节水床效应的目的。

1 双梯度算法

1.1 自适应反馈有源噪声控制系统

自适应反馈控制系统目前采用较多的是基于内模型控制(Internal model control IMC)结构[2]。IMC结构其实是一个预测器，因为实际系统只可能获取当前采样点的误差信号和次级信号，然后估计出下一采样点的噪声信号作为输入控制器的参考信号。

如图1所示，d(n)、e(n)和y(n)分别为系统的初级噪声信号、误差传感器采集的噪声信号和控制器输出的次级信号，W(z)为控制器，S(z)为次级路径传递函数。在z域中，初级噪声可表示为

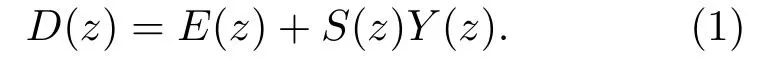
如果次级路径的传递函数S(z)可以估计得到，并且S(z)≈则能估计出初级噪声d(n)并将其作为参考信号x(n)，

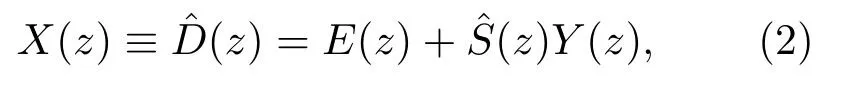
图1 自适应反馈控制系统框图Fig.1 Block diagram of adaptive feedback control system

经典滤波最小均方(Filtered-x least mean square FxLMS)算法采用最小均方误差准则，设定控制系统目标函数

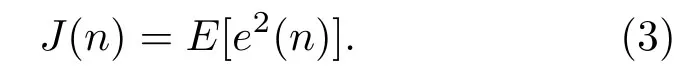
用梯度下降法得到控制器w(n)的迭代算法：

其中，µ为收敛系数，L为控制器系数的阶数。x′(n)为滤波参考信号，即

“Leaky”算法在目标函数中引入惩罚项“γwT(n)w(n)”限制控制器的输出和保持算法的稳定性，其代价函数

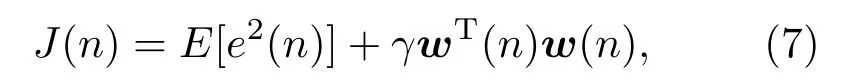
其中，0<γ <1。其控制器系数迭代公式为

“Rescaling”算法不改变FxLMS算法的目标函数，而是在违反约束情况下沿着约束边界将梯度投影到约束集中[12]，即

当|y(n+1)|≤C时，

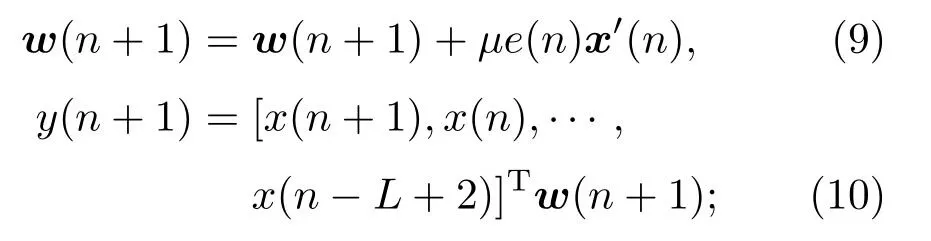
当|y(n+1)|>C时，

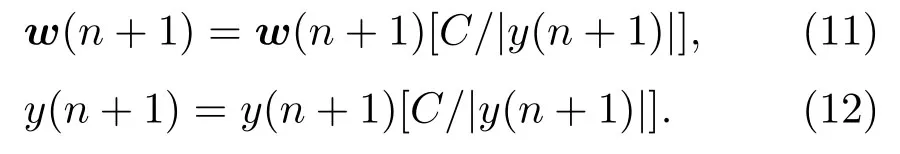
1.2 双梯度算法

本文提出的双梯度FxLMS(Double-gradient FxLMS,DGD-FxLMS)算法是通过直接约束次级信号来改善水床效应的噪声放大问题，当次级信号超出约束时将次级信号的均方作为目标函数，最小化次级信号的能量。

设定目标函数

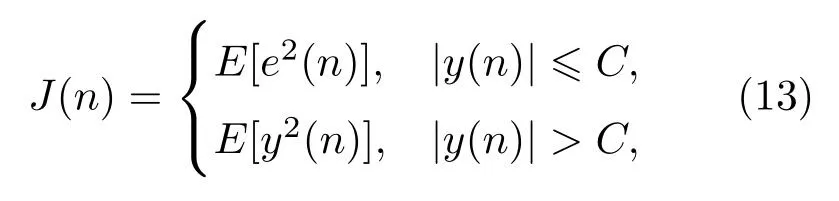
其中，

按照最陡下降法递推滤波器的最佳权系数

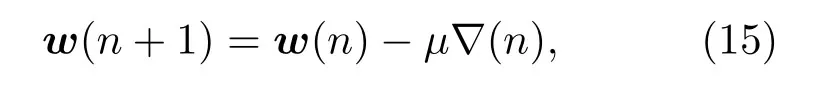
所以，滤波器权矢量迭代公式

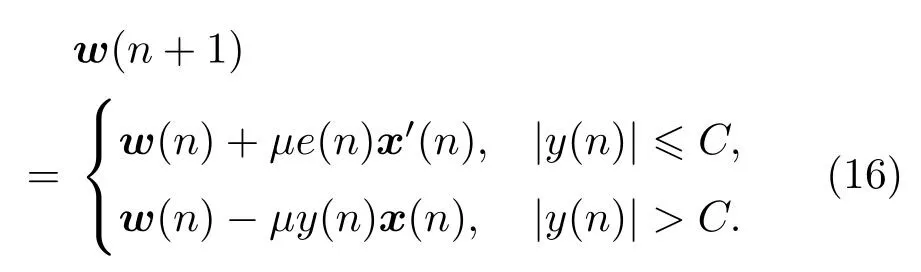
该算法沿着两个梯度方向搜索最佳权矢量，其主要流程如表1所示。

表1 DGD-FxLMS算法Table1 Pseudo code of DGD-FxLMS algorithm

1.3 计算复杂度

对于“FxLMS”、“Leaky”、“Rescaling”、“DGDFxLMS”4种自适应算法，表2对其计算量进行比较。4种算法计算复杂度比较主要包括3个部分：(1)计算次级信号y(n)；(2)用估计的次级路径对初级信号x(n)进行滤波；(3)滤波器权矢量的迭代更新[14]。从表2中可知，就加法、乘法和除法计算量而言，对于一个样本点，当控制器输出超过约束时，“DGD-FxLMS”算法比“FxLMS”算法少一次次级路径滤波，即少P次乘法和(P−1)次加法；当控制器输出不超过约束时，“DGD-FxLMS”算法与“FxLMS”算法计算量相同。虽然“DGD-FxLMS”算法还需要一些额外的选择开关以及一个阈值门阀，可以通过条件语句控制，而条件语句通常只需很少的机器周期，所以与传统的“FxLMS”算法相比，“DGD-FxLMS”算法多余的计算复杂度可以忽略不记。与“Leaky”算法相比，“DGD-FxLMS”算法少L或(L+P)次乘法，少0或(P−1)次加法。与“Rescaling”算法相比，“DGD-FxLMS”算法少(L+1)或(L+P+1)次乘法，少0或(P−1)次加法，少0或1次除法。因此，本文算法的计算量较小。

表2 4种算法的主要计算量Table2 Computation load of the four algorithms

2 仿真验证

2.1 实验设置

本文验证了4种算法在有源降噪耳机中的实际效果。如图2所示，将市场上购买的有源降噪耳机用作原型佩戴到B&K公司的人工头(4182C)上，在保持耳机整体结构不变的情况下拆分引出误差传感器、次级信号线，将误差麦克风通过传声器前放连接到B&K公司的Pulse上，Pulse一方面将误差信号与次级信号输送到电脑，另一方面也将噪声信号传送给扬声器(初级噪声源)。

图2 有源降噪耳机实验系统的器件连接Fig.2 The devices connection in the active noise control headphone experiments

实验在全消声室中进行，如图3(a)所示，初级声源分别位于人工头正前方、正左方、正右方和正后方，距离人工头0.3 m。系统的采样率为16 kHz。采用最小均方误差(Least mean square LMS)算法估计出次级路径，此处为256阶有限长脉冲响应(Finite impulse response,FIR)滤波器。

图3 初级声源的4个位置及消声室中的实验场景Fig.3 Diagrammatic view of the 4 different incident directions of the primary noise and the experimental configuration in the anechoic chamber

2.2 结果与讨论

本文以降噪量评价降噪性能的好坏，降噪量为ANC系统关闭与打开两种情况下误差传感器信号的功率谱密度之差。实验分别对4个不同入射方向进行降噪性能测试，发现左右两只耳朵的性能几乎一样，为了在一幅图中更加清晰简洁地看出每种算法的降噪量，取右耳4个不同入射方向初级噪声源的降噪量的平均值进行对比。

本文选用“FxLMS”、“Leaky”、“Rescaling”、“DGD-FxLMS”4种算法分别迭代得到4种控制器后，对比4种算法的降噪量，后3种算法均为经典“FxLMS”的改进算法，可以限定控制器的幅度输出。控制器W(z)都为FIR 滤波器，4种算法的参数设定于表3中，“FxLMS”算法中µ=0.003；“Leaky”算法中µ=0.004，γ=0.05，相当于泄漏因子为0.9998；“Rescaling”算法中µ=0.004，C=0.005；“DGD-FxLMS”算法中µ=0.003，C=0.001。

表3 4种算法的参数设定Table3 Parameter settings of the four algorithms

4种算法的降噪量如图4所示，可以看出“Leaky”算法和“Rescaling”算法的有效降噪频段分别在660 Hz和740 Hz以下，而“FxLMS”和“DGDFxLMS”算法在1000 Hz 还有降噪。“FxLMS”算法在235 Hz附近可以获得21 dB的最大降噪量，同时它在2000∼4000 Hz频段内的噪声放大也是最大的，其噪声放大在2∼7 dB；“Leaky”算法在250 Hz附近获得8 dB的最大降噪量，其噪声放大量是最小的，都低于2 dB 且均匀分布在1000∼5000 Hz范围内，但“Leaky”算法的有效降噪频段是最窄的；“Rescaling”算法在235 Hz附近获得15 dB的最大降噪量，尽管“Rescaling”算法在430 Hz以下频段的降噪量大于“DGD-FxLMS”算法，其在1000∼2200 Hz频段的噪声放大量大于“DGDFxLMS”算法，并且“Rescaling”算法有效降噪频段比“DGD-FxLMS”算法窄。“DGD-FxLMS”算法在300 Hz附近获得9.5 dB的最大降噪量，其有效降噪频段几乎和“FxLMS”算法的有效降噪频段重合。

图4结果表明“DGD-FxLMS”算法在最大降噪量上比“FxLMS”算法和“Rescaling”算法差，从式(3)可以看出“FxLMS”算法在搜索最佳权矢量过程中没有考虑其他任何约束条件，而仅仅以将误差信号能量降到最低为目标，因此它虽然最大降噪量高，噪声放大也最大。

“Rescaling”算法效果较好，既有不错的降噪量，噪声放大也不大，但从式(11)和式(12)来看，在实际的数字信号处理器件应用中，除法运算会消耗较大资源，此外，该算法是采用“硬性”削波的方式对次级信号进行处理，没有明确的代价函数。

从降噪量和有效降噪带宽来看，“DGD-FxLMS”算法在降噪性能上优于“Leaky”算法。从式(7)知“Leaky”算法引入惩罚项“γwT(n)w(n)”，所以式(8)“Leaky”算法每次更新控制器系数时都对其进行约束，但“Leaky”算法不同于“Rescaling”算法，“Rescaling”算法在控制器超过约束时仅硬乘一个标量[C/y(n+1)]，相当于将L个控制器系数等比例缩小，而“DGD-FxLMS”算法则在控制器超过约束时根据x(n)的大小“软性”决定系数调节的大小，L个控制器系数中有些可能被缩小，有些可能被放大，相当于对整个滤波器做整形，其调节的自由度更大，也更精确。

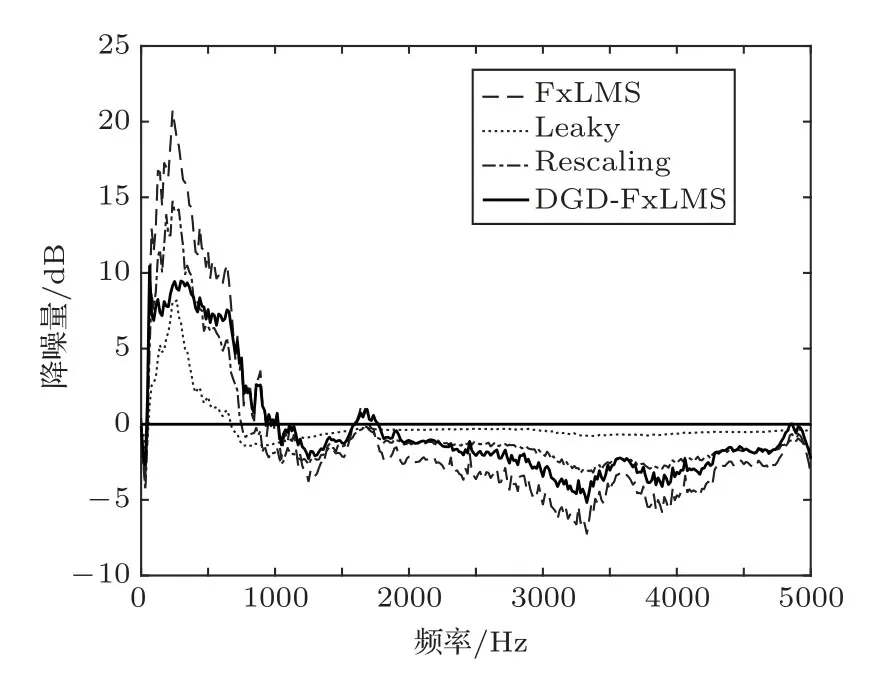
图4 4种算法的降噪性能Fig.4 The ANC performance of four algorithms

在自适应控制过程中“DGD-FxLMS”算法在梯度1和梯度2两个梯度方向的分布比例分别为62.4%和37.6%，梯度1和梯度2是指分别沿式(13)上下两行目标函数的方向寻求最佳权矢量。表明“DGD-FxLMS”算法在最小化误差能量的同时兼顾了噪声放大。图5给出了4种算法的误差收敛曲线，从图5中可以看出，与其他3种算法对比，尽管“DGD-FxLMS”算法会在两个梯度方向上进行切换，但并不会在收敛过程中出现系统不稳定性问题。

图5 4种算法的收敛曲线Fig.5 Convergence curves of the four algorithms

3 结论

约束控制器输出幅度可以改善水床效应中的噪声放大现象。本文以控制器的实际输出是否超出约束作为选择目标函数的依据，研究了一种“DGDFxLMS”算法：当控制器输出满足约束，该算法沿着最小化误差信号能量的梯度方向迭代；反之，则沿着最小化次级信号能量的方向迭代。在有源降噪耳机实例中的验证结果表明该算法可以在保证一定降噪量情况下改善噪声放大问题，同时其运算量是实际应用可以接受的。