四阶带通箱的自回归滑动平均模型∗

陈 立 田 兴 夏 洁 沈 勇

(南京大学声学研究所 近代声学教育部重点实验室 南京 210093)

0 引言

数字信号处理技术现已广泛应用于扬声器系统之中，以实现均衡、过载保护、参数辨识、失真补偿等诸多功能[1−2]，达到提升音质、优化性能的目的。这些功能都要依托于前馈式数字控制器来实现，这要求对扬声器系统建立稳定而精确的离散时间模型，实时地预测扬声器系统的状态量，供给数字处理模块，使其正常工作。

建立扬声器系统的离散时间模型主要有两种方法。一是建立扬声器系统的状态空间方程(Statespace,SS)，运用差分方法进行求解[3−4]；二是基于系统传递函数，构建其自回归滑动平均(Autoregressive moving average,ARMA)模型。SS模型原理简单，但对采样率要求较高，稳定性差，精确程度不足。ARMA模型对采样率的要求低，稳定性好，相比于SS模型更加精确，且由于其等价于无限冲激响应(Infinite impulse response,IIR)滤波器，适用自适应滤波器理论，因此应用更广。

许多学者在建立扬声器系统的ARMA模型方面做了工作。Kundsen等[5]从扬声器振膜速度的传递函数出发，将扬声器单元模型等效为一个自适应滤波器，建立时域差分方程，得到其集总参数类比线路图力学端的离散时间模型；Bright[6−7]在忽略电感的情况下给出了扬声器单元类比线路图电学端的时域迭代公式，将其用于辨识，取得了很好的效果；朱志鹏等[8]进一步对Bright的模型进行优化，在电学端加上了等效电感，提高了离散时间模型的精确程度。

然而上述的ARMA模型对于音圈电感的建模仍然较为简单，模型精确程度不足。且它们都是针对简单的扬声器单元或者封闭箱系统，对四阶带通箱这种体积小、效率高、声学端负载相比单元更复杂的扬声器系统[9−10]的建模工作，还是停留在使用前向欧拉法建立SS模型，对仿真采样率要求较高，计算代价较大。

本文进一步使用LR-2理论[11]对音圈电感进行优化，并且就具有复杂声学端负载的四阶带通箱建立ARMA模型。从四阶带通箱的状态空间方程出发，给出其集总参数模型的系统传递函数方程组，将其离散化后得到时域差分迭代式。通过实验将本文给出的ARMA模型与SS模型进行对比，说明ARMA模型更加稳定与精确，因此更具应用价值。

1 理论分析

1.1 四阶带通箱模型

四阶带通箱是声学带通滤波器阶数为四的扬声器系统，扬声器单元镶嵌在箱体内部隔板上，系统辐射声源为声导管，其结构示意图如图1所示。在建立扬声器系统集总参数类比线路图时，使用Klippel提出的LR-2理论对其进行优化，在模型中增加了串联次级电感电阻，其等效类比线路图如图2所示。

图2中模型参数与状态变量说明如下：

模型参数：

RE—扬声器单元音圈直流电阻；

LE—扬声器单元音圈等效电感；

L2—音圈副电感；

R2—音圈涡流电阻；

Bl—扬声器单元的力电耦合因数；

RMS—包含空气负载的扬声器单元的等效力阻；

MMS—包含空气负载的扬声器单元振动系统的等效质量；

CM—扬声器单元悬置系统和腔体1 内空气的总等效力顺；

S—扬声器单元振膜的有效辐射面积；

CAB2—腔体2内空气的等效声顺；

MAP—声导管的等效声质量；

RAP—声导管的等效声阻。

状态变量：

u—扬声器系统两端电压；

i—流经扬声器单元音圈的电流；

i2—流经音圈副电感的电流；

v—扬声器单元振膜的振动速度；

US—腔体1空气的容积速度；

UP—声导管内空气的容积速度；

pa—声导管所在腔体的声压。

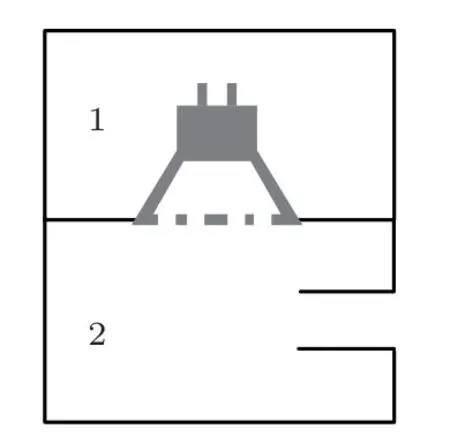
图1 四阶带通箱的结构示意图Fig.1 Schematic drawing of the fourth-order band-pass loudspeaker system

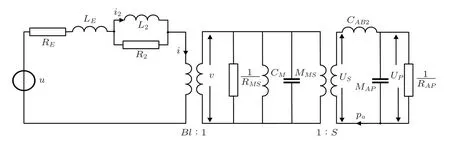
图2 四阶带通箱集总参数模型的类比线路图Fig.2 Equivalent circuit of the fourth-order band-pass loudspeaker system

与之对应的四阶带通箱的状态空间方程写为

1.2 系统模型离散化

基于状态空间方程式(1)使用前向欧拉法进行仿真得到的系统离散时间模型即SS模型。前向欧拉法是基于前向差分法对传递函数进行离散化的，这种方法基于积分的矩形法则，较为简单但是畸变严重、等效精度较差，且只能将s左半平面的一个有限半径的圆映射到z平面的单位圆，所以当s域传递函数稳定时，z域传递函数不一定稳定；而双线性变换法与零极点匹配法精度较高、频率特性保真度较好，当s域传递函数稳定时，z域传递函数一定稳定[12]。因此下文将状态空间方程改写成传递函数的形式，利用双线性变换法和零极点匹配法对其进行离散化，建立系统的ARMA模型。

将状态空间方程改写成偏微分方程组并对其进行拉普拉斯变换，将电学端、力学端、声学端状态量合并，得到用3个系统状态量i、v、pa表示的传递函数方程组：

其中，L−1表示求逆拉普拉斯变换，∗为卷积符号。

提取其中的s域传递函数：

使用双线性变换法将电学s域传递函数离散化，使用零极点匹配法将力学和声学s域传递函数离散化，得到z域传递函数及时域差分方程：

其中，z域传递函数和时域差分方程的系数可由扬声器系统各参数、力学端振动系统的阻尼比和归一化共振角频率声学端振动系统的阻尼比和归一化共振角频率离散化的时间采样间隔ts共同给出，具体表达如下：

时域差分方程组式(6)即为期望得到的四阶带通箱的ARMA模型。

1.3 极点分布

考察式(4)，探究3个s域传递函数极点分布。

对电学端传递函数，其s域极点λi为

考虑到实际物理意义，式(10)中各参数都是正数，因此限定了极点分布的范围，其分子实部为

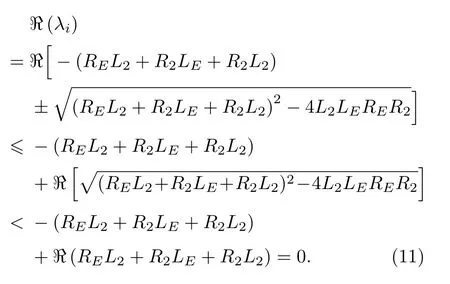
同理，力学端和声学端s域传递函数分子实部为

三个s域传递函数极点均分布在s平面左半平面，所以都稳定。而双线性变换法和零极点匹配法的特性是若s域传递函数稳定，z域传递函数一定稳定[12]，即式(5)∼(6)给出的z域传递函数和时域差分方程稳定，本文给出的ARMA模型稳定。

2 实验验证

2.1 实验对象

为验证给出的ARMA模型理论的正确性，研究设计并进行了四阶带通箱的相关实验。该四阶带通箱外尺寸为27 cm×16 cm×18 cm，内部镶嵌一个11.67 cm(3.5 寸)扬声器单元，其系统参数由KLIPPEL 电声测量仪测得。四阶带通箱的正视图和侧视图如图3所示。

图3 四阶带通箱的正视图和侧视图Fig.3 Face view and side view of the fourth-order band-pass loudspeaker system

2.2 实验测量

测量实验在南京大学消声室进行，四阶带通箱安装在KLIPPEL测试架上(无障板条件)。测量仪器为B&K PULSE系统和SoundCheck电声测量仪。本实验使用粉红噪声信号激励四阶带通箱以获取其电学数据，激励电压为3 V，激励时长为5 s。

2.3 实验结果

使用B&K PULSE系统获取四阶带通箱的实测电压与电流，计算其自功率谱与互功率谱，得到电学传递函数，形成实测阻抗曲线；在录回的电流数据中随机截取连续200个采样点的数值，得到四阶带通箱的瞬时电流波形。使用KLIPPEL 电声测量仪获取四阶带通箱的参数，基于集总参数模型计算得到阻抗曲线的理论值。

基于测量得到的模型参数，在相同的激励信号和采样率(24 kHz)下，分别建立四阶带通箱的SS模型和ARMA模型。计算模型输出电压与电流的自功率谱与互功率谱，获取其电学传递函数，得到仿真的阻抗曲线；截取模型输出电流数据中对应于实测的200个采样点的数值，得到四阶带通箱离散时间模型的瞬时电流波形。

绘制实测的与理论的阻抗曲线，如图4所示。绘制实测的与两模型输出的阻抗曲线，如图5所示。绘制实测的与两模型输出的阻抗曲线的误差绝对值，如图6所示。绘制实测的与两模型输出的瞬时电流波形，如图7所示(为直观清楚起见，仅展示头100个采样点)。绘制实测的与两模型输出的电流波形的误差绝对值，如图8所示。计算两模型输出阻抗曲线、电流波形与实测值误差的均方根值，如表1所示。

图4中，理论值与实测值吻合得较好，说明KLIPPEL 测量仪的测量结果准确可靠，实验误差较小，基于该测量参数进行建模是有意义的。在图5、图6和表1中，ARMA模型的输出阻抗曲线相比于SS模型与实测数据吻合得更好，误差更小；在图7、图8和表1中，ARMA模型的输出电流波形相比于SS模型与实测数据吻合得更好，误差更小。说明在相同的采样率下，ARMA模型无论是在全频带的工作性能还是瞬时工作性能，都要优于SS模型。

图4 理论与实测的阻抗曲线Fig.4 Theoretical and measured impedance curves

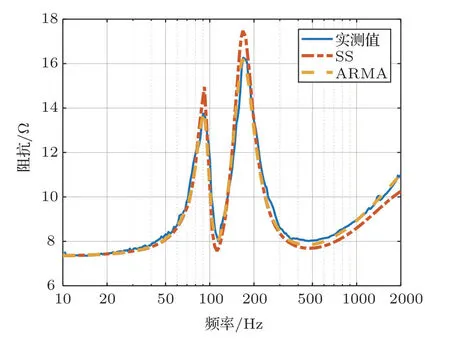
图5 模型输出阻抗曲线Fig.5 Impedance curve from the models

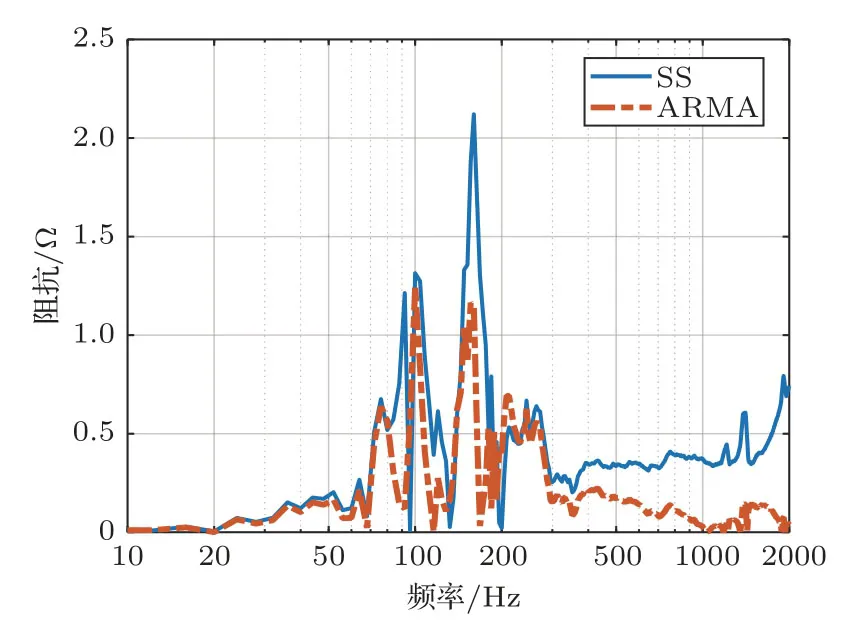
图6 阻抗曲线误差Fig.6 Error of impedance curves

表1 阻抗和电流曲线误差Table1 Errors of impedance and current curves

图7 模型输出电流波形Fig.7 Current waveform from the models

图8 电流波形误差Fig.8 Error of current waveforms

为进一步研究ARMA模型对于采样率的要求，在不同的采样率下，分别建立四阶带通箱的SS模型和ARMA模型，对同样的输入电压信号，比较其输出电流信号与实测电流信号的误差的均方根值，结果如表2所示。当采样率小于等于20 kHz时，SS模型发散，无法正常工作，而ARMA模型在5 kHz及以上的采样率下均能稳定工作；在同一采样率下，ARMA模型的误差均显著小于SS模型的误差；在同样的精度要求下，ARMA模型所需的采样率低于SS模型的要求。上述结果说明，ARMA模型对采样率要求更低、稳定性更强、精确程度更高。

表2 电流误差Table2 Errors of current curves

3 结论

本文研究了四阶带通箱的离散时间模型，提出了用于预测和控制四阶带通箱瞬态行为的自回归滑动平均模型，并进行了实验验证。实验结果表明，与基于状态空间方程的差分求解方法相比，该模型在采样率相同的前提下明显提升了精确程度，在保证稳定的前提下明显降低了对采样率的要求。

该离散时间模型具有良好的稳定性与精确性，其形式简单，适用于自适应滤波理论。基于此模型，可以实现对四阶带通箱的过载保护、自适应参数辨识与失真补偿，从而帮助提升四阶带通箱的工作表现。