基于遗传算法优化支持向量机的大坝安全性态预测模型

谷艳昌，吴云星，黄海兵，庞 琼

(1.南京水利科学研究院大坝安全与管理研究所，江苏 南京 210029； 2.水利部大坝安全管理中心，江苏 南京 210029)

我国共有水库9.8万余座，其中土石坝占绝大部分。近年来，大坝安全越来越受到重视，大坝安全早期预警需求也越来越迫切[1-2]。如何根据大坝安全监测数据，挖掘大坝潜在安全运行信息，实现大坝安全准确预警，对于大坝安全应急管理非常重要。目前，在大坝安全预测预警领域，主要有传统方法和智能方法。传统方法有统计模型、确定性模型、混合模型，智能方法诸如支持向量机(support vector machines，SVM)模型[3]、神经网络模型[4]、小波分析[5]等已得到广泛应用。其中支持向量机模型基于结构风险最小原理，能有效地解决小样本、高维数、非线性的问题，具有良好的泛化能力[6-9]。但支持向量机精度与惩罚参数c和核函数参数g密切相关，其参数优化方法有传统的k-折交叉验证法(k-CV)、遗传算法(GA)[10-11]、粒子群算法(PSO)[12-13]、人工蜂群算法(ABCA)[14]、布谷鸟搜索算法(CS)[15]等启发式算法。传统的支持向量机在k-CV意义下，采用网格划分寻找最佳参数，其可以有效避免过学习和欠学习状态的发生，但同时存在精度低、在更大范围内参数寻优费时等缺点[16]。遗传算法是一种适合复杂系统优化的自适应概率优化技术，收敛性快、精度高，寻优能力和适应性强[17]，可以不必遍历网格内的所有参数点，即能搜索到全局最优解，目前在参数寻优中应用普遍。

为提高大坝安全性态预测效果，本文采用遗传算法对支持向量机的惩罚参数c和核函数参数g进行优选，以影响量和效应量历史监测数据对支持向量机进行训练，建立GA-SVM预测模型，并拟定大坝安全性态三级指标和判别准则。将GA-SVM模型应用于实际工程的渗流性态预测中，以验证该模型的有效性。

1 支持向量机和遗传算法基本原理

1.1 支持向量机

支持向量机是由Cortes等于1995年正式提出的[18]，其可以通过少量样本解决非线性高维空间问题，具有良好的分类能力和预测性能。支持向量机原理如下：

设有一组训练样本(x1,y1)，(x2,y2)，…，(xi,yi)∈(Rn×R)，采用非线性映射φ(x)将样本映射到更高维的特征空间，在更高维空间构造最优线性函数f(x)=ω·φ(x)+b。根据结构风险最小化原则寻找合适的ω、b，为了降低模型复杂程度，提高泛化能力，寻优过程等价于式(1)(2)：

(1)

s.t.yi=ωT·φ(xi)+b+ξi(i=1,2,…,l)

(2)

式中：ω——权向量；c——惩罚参数，c>0；ξ——松弛变量，用来衡量训练样本偏离程度；b——常数；l——训练样本数。

为实现上述优化问题，建立Lagrange函数：

(3)

式中：αi——Lagrange乘子。

根据最优解KKT(Karush-Kuhn-Tucker)条件：

(4)

可得

(5)

定义核函数K(x,xi)满足Mercer条件，消去ξi和ω之后，可得到如下线性方程组：

(6)

其中e=[1,1,…,1]Tα=[α1,α2,…,αl]TQij=K(xi,xj) (i,j=1,2,…,l)

式中：I——单位矩阵。

就核函数而言，只要满足Mercer条件的均为核函数。常见的核函数有线性函数、Sigmoid函数、多项式函数和高斯径向基(RBF)函数等，其中RBF函数应用最为广泛，无论大样本还是小样本都有比较好的性能。本文SVM算法的实现采用LIBSVM工具箱，选取RBF函数作为核函数：

(7)

式中：x——函数中心；g——核函数参数。

最终得到的回归模型如下：

(8)

根据以上支持向量机原理可知，惩罚参数c和核函数参数g是影响支持向量机预测性能的关键因素。

1.2 遗传算法

遗传算法把问题的解编码为染色体，再通过创建适应度函数，按适应度函数值的概率分布筛选出高适应度值的个体，然后再进行选择、交叉和变异等操作来交换种群中染色体的信息，最终产生符合优化目标的染色体(最优解)[19]。

a. 创建适应度函数。适应度函数是个体适应环境能力的表达，其与目标函数有关，本文以均方误差作为目标函数。由于遗传算法只能向着使适应度值增大的方向进化，因此适应度函数采用均方误差的倒数形式。

b. 选择。从上一代群体中按一定概率选择优秀个体(适应度值大的个体被选中的概率大)，组成新的种群。个体被选中的概率为

(9)

式中：ps——个体被选中的概率；Fs——个体适应度值；N——种群数量。

c. 交叉。从种群中随机选择2个个体，以交叉概率β(位于[0，1]区间)进行染色体交换，并将优秀的特征遗传给下一代，经交叉运算产生的子代替其父代。2个个体ak、al在z位的交叉运算为

(10)

d. 变异。首先随机地从种群中选择一个个体，然后以一定的概率对个体的某个基因进行变异，从而保持群体中基因的多样性。第u个个体的第v个基因进行的变异操作为

(11)

式中：amax、amin——基因auv的上界、下界；r——[0，1]间的随机数；r1——随机数；G——当前进化代数；Gm——最大进化代数。

2 GA-SVM大坝安全性态预测模型

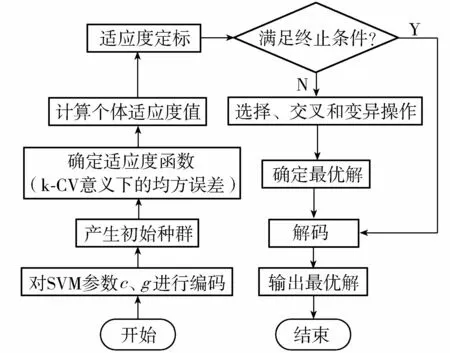
图1 遗传算法优化SVM参数c和g流程Fig.1 Optimization procedure of SVM parameters c and g by genetic algorithm

2.1 遗传算法参数寻优

遗传算法优化SVM的惩罚参数c和核函数参数g的实现过程见图1。具体步骤为：(a)对惩罚参数c和核函数参数g进行二进制编码，产生初始种群。(b)设定遗传算法最大进化代数、交叉概率和变异概率。(c)以k-CV意义下的均方误差的倒数作为适应度函数，并计算个体的适应度。(d)判断是否满足终止条件，即进化次数是否达到最大进化代数。若达到最大进化代数，则遗传算法运行终止，输出最优解;否则，进行以下步骤。(e)采用轮盘赌法进行选择操作，而后进行交叉和变异操作。(f)将所有个体中适应度最高的个体作为最优解，并解码后输出。

2.2 GA-SVM预测模型

2.2.1GA-SVM预测模型构建

根据实际需要，选定模型输入(如库水位、温度、降雨、时效等)和输出变量(如变形、渗流压力等)，将用于分析的历史数据分为训练样本和测试样本，然后将遗传算法寻优得到的最佳c和g赋予支持向量机进行训练，最后将训练好的模型对未来数据进行回归预测，即为GA-SVM大坝安全性态预测模型。

2.2.2 大坝安全性态判别准则

由于库水位、降雨等影响因素具有随机性，因此受其影响的大坝效应量也具有随机性。对于已运行时间较长的大坝，积累的监测数据量较为充分，大坝效应量的变化近似服从正态分布[20]。

根据概率统计理论中的3σ准则，对于一个具有正态或近似正态分布的样本，其数值分布在(μ-σ，μ+σ)中的概率为0.682 6，分布在(μ-2σ，μ+2σ)中的概率为0.954 4，分布在(μ-3σ，μ+3σ)中的概率为0.997 4[21]。据此，可根据3σ准则制定大坝安全性态三级指标，即μ+σ、μ+2σ和μ+3σ。μ、σ分别为GA-SVM模型的均值和标准差。

大坝运行安全性态级别分4级，若y′为某一时刻由预测模型得到的效应量预测值，则：(a)当y′<μ+σ时，为正常；(b)当μ+σ≤y′<μ+2σ时，为基本正常；(c)当μ+2σ≤y′<μ+3σ时，为异常；(d)当y′ ≥μ+3σ时，险情很可能发生。

2.2.3 基于GA-SVM模型的大坝安全性态判别

GA-SVM大坝安全性态预测模型的实现流程见图2。

图2 GA-SVM大坝安全性态预测模型实现流程Fig.2 Realization process of GA-SVM prediction model for dam safety behavior

3 某水库大坝渗流安全性态预测

某水库正常蓄水位21.16 m，100年一遇洪水位24.60 m，1 000年一遇设计洪水位25.62 m，PMP校核洪水位27.72 m，死水位16.68 m。大坝为均质土坝，坝顶长2 222 m，坝顶宽6 m，最大坝高为24.00 m，坝顶高程为28.70 m。

3.1 数据选取和预处理

3.1.1 确定输入和输出变量

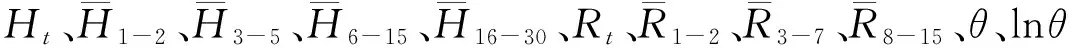
3.1.2 训练和测试数据选取

以该坝B0500A测点为例，对本文建立的GA-SVM模型进行适用性分析。B0500A测点位于桩号0+500距坝轴线12 m处，测点高程为12.58 m。

通常情况下，输入数据越多，训练后的模型越能反映输入输出关系，但数据太多会增加计算量，导致模型收敛偏慢，而数据过少则有可能达不到理想的预测效果。另外，受到环境和仪器本身因素的影响，效应量监测数据往往由真实值和观测误差(噪声)组成，若直接采用未经消噪的观测数据对支持向量机进行训练会影响模型的稳定性，因而需事先对所选样本数据进行去噪处理，提高数据序列的光滑度。鉴于此，选取2010年1月1日至4月10日共100期的库水位、降雨数据作为训练样本的输入，将经小波消噪后的渗流压力值实测数据作为训练样本的输出，其过程线见图3。将2010年4月11—20日共10个期次的实测数据作为测试样本。

3.1.3 数据标准化处理

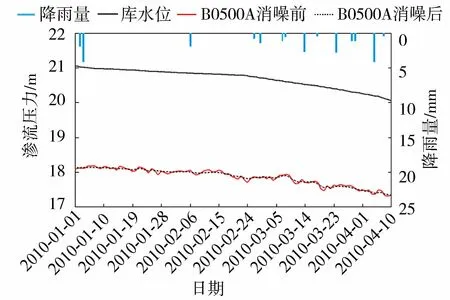
图3 B0500A测点渗流压力与库水位和降雨过程线Fig.3 Hydrograph of reservoir water level, rainfall and B0500A observed seepage pressure

图4 遗传算法优化SVM参数适应度曲线Fig.4 Fitness curve of SVM parameter in the optimization process by genetic algorithm

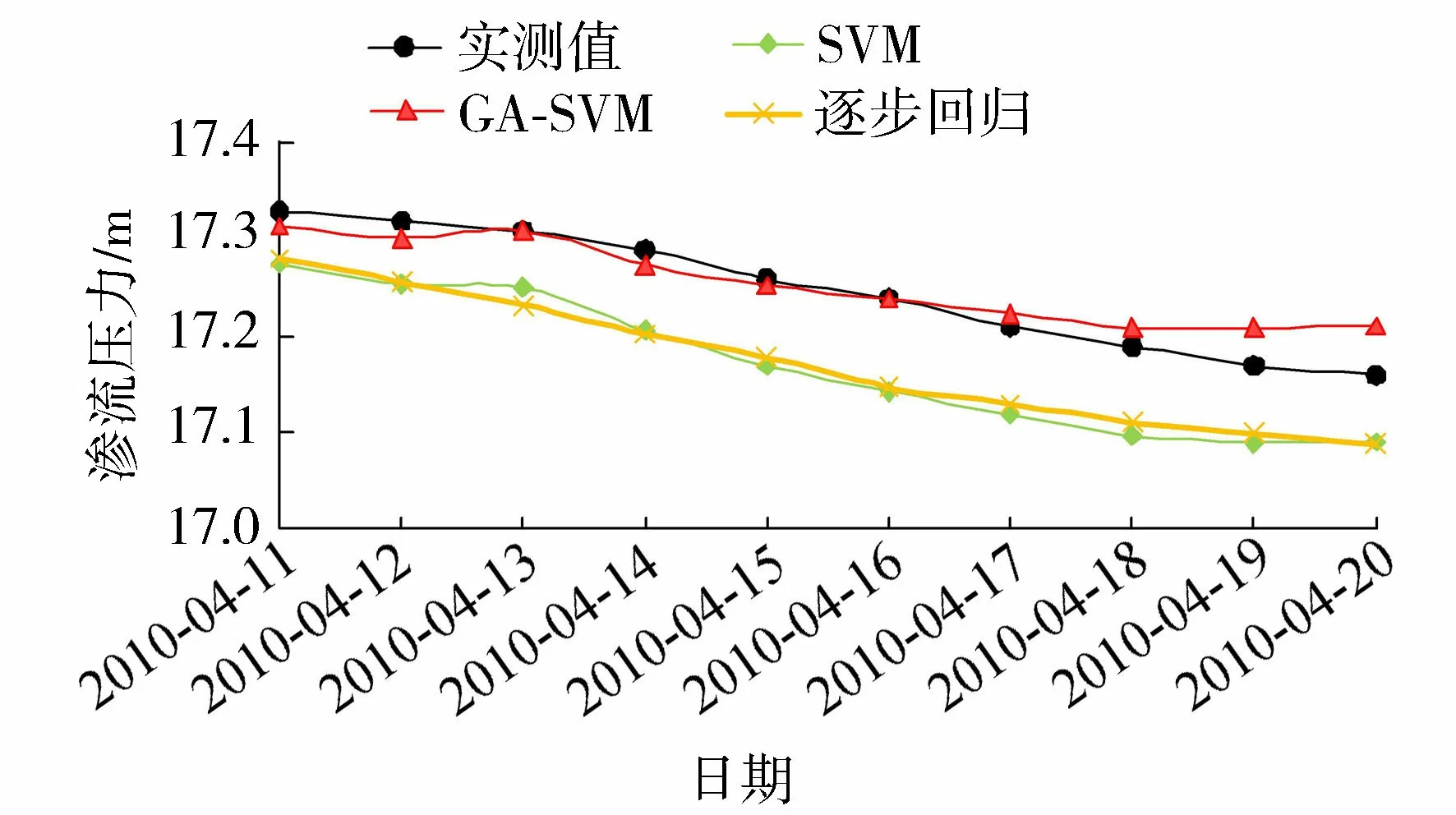
图5 各模型渗流压力预测值过程线Fig.5 Curves of predicted seepage pressure by different models

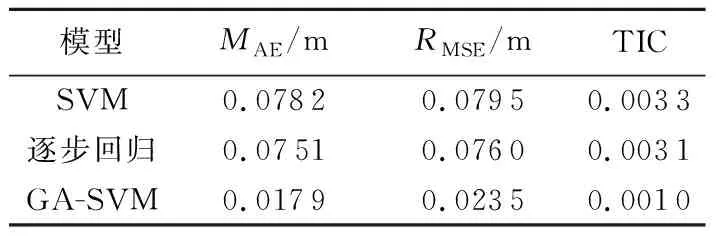
表1 3种模型预测精度对比

为加快学习速度，需对数据进行标准化处理：X′=0.1+0.8(X-Xmin)/(Xmax-Xmin)。其中：X′为标准化后的值，其值介于[0.1，0.9]之间；Xmax、Xmin分别为样本中每组数据的最大值与最小值。

3.2 参数设置

为了对GA-SVM模型的预测效果进行横向比较，本文同时建立了SVM模型和逐步回归模型。GA-SVM模型采用遗传算法优化惩罚参数c和核函数参数g，SVM模型采用k-CV法对参数进行优化，其他参数采用默认值。遗传算法参数设置为：最大进化代数取100，种群数量取50，代沟取0.9，k-CV参数取5，c介于[0，100]，g介于[0，100]，交叉概率和变异概率均取0.7。

3.3 模型预测性能评价标准

采用平均绝对误差(MAE)、均方根误差(RMSE)和希尔不等系数(TIC)评价各预测模型的性能。平均绝对误差可以较好地反映预测精度，其越小，预测精度越高。均方根误差可以较好地衡量不同模型预测误差间的微小差别，其值越小越好。希尔不等系数是评价预测值相对实测值拟合误差的指标，介于[0，1]之间，越接近0，表示拟合误差越小，计算公式见文献[12]。

3.4 预测结果分析

基于MATLAB R2014a平台，采用LIBSVM-3.22工具箱，利用遗传算法优化支持向量机c和g，经多次运行，得出较佳的适应度曲线，其变化过程见图4。

经遗传算法优化得到的最佳参数c=98.815 9，g=0.016 403，然后赋予支持向量机并用训练样本进行训练，再将测试样本输入训练好的模型中进行预测。3种模型预测值及预测值过程线见图5。

由图5可知，GA-SVM模型预测值较SVM模型和逐步回归模型预测值更接近实测值，且其过程线整体变化趋势与实测值变化过程相似，能较为真实地反映大坝渗流压力的变化情况。SVM模型和逐步回归模型预测值相差不大，预测值过程线变化趋势与实测值变化过程大体相似，但预测效果均劣于GA-SVM模型。随着预测期数的增加，从第8期开始，GA-SVM模型预测值过程线开始偏离实测值过程线，预测误差明显增大，这是由于老数据刻画系统演化的作用在逐步降低。因此，使用同一个训练样本对SVM训练后预测期数不宜过多，且随着预测期数的推移需不断加入新的数据，以增强模型的预测效果。

各模型的预测精度比较见表1。GA-SVM模型无论从平均绝对误差(MAE)、均方根误差(RMSE)还是希尔不等系数(TIC)均小于SVM模型和逐步回归模型，反映出其预测效果较为理想，可以满足大坝渗流预测的需要。

GA-SVM模型均值μ为17.85，标准差σ为0.22。由3σ准则计算得到的B0500A测点的渗流压力三级安全性态指标分别为μ+σ=18.07 m、μ+2σ=18.29 m和μ+3σ=18.51 m。在预测时段内，由GA-SVM模型得到的B0500A测点渗流压力预测值均小于18.07 m，因此大坝渗流性态正常，后续继续观测。

4 结 论

a. 惩罚参数c和核函数参数g是影响支持向量机预测性能的关键因素，采用遗传算法进行参数寻优，有效地克服了k-CV法参数选择时精度低、不易全局优化的缺点。

b. 本文建立的GA-SVM模型成功地预测了大坝渗流压力，平均绝对误差仅为0.017 9、均方根误差为0.023 5、希尔不等系数为0.001 0，其预测精度较SVM模型和逐步回归模型提高了3倍左右。但预测期数不宜过多，需不断加入新的数据进行训练，以使模型的预测效果更佳。

c. 基于GA-SVM模型预测结果，根据大坝渗流安全性态三级指标和四级判别准则，合理判定了大坝渗流安全性态。