基于FDA的大坝渗流安全动态可拓评价模型

吕 鹏，王晓玲，余红玲，王 成，刘长欣

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

在大坝运行过程中，渗流是影响大坝安全的重要因素之一[1-3]，受内外综合因素的影响，分析评价大坝渗流安全状态难度较大[4-5]。近年来，物联网技术在水利工程安全监测中得到广泛应用[6-7]，使得自动获取大量、复杂的渗流安全监测数据成为现实，这些监测数据的采集虽然是离散的，但融合了横截面数据与时间序列数据特性，具有函数的特性，被称为函数型数据[8]。目前，大坝渗流综合评价方法主要有层次分析法、模糊数学法、人工神经网络法和灰色聚类法等[9]，这些方法多是对离散数据直接进行分析，所使用的信息及得到的结论往往都是间断的，失去了大量的有效信息，而且太过依赖模型的线性结构和假设条件。由于各指标的特性不同，其采集频率也不尽相同，同时检测仪器所处环境复杂，仪器本身存在可靠性问题，会出现某时刻或某段时间数据缺失的现象，导致评价模型失效。因此，建立一种适用于函数型数据的大坝渗流安全动态连续评价模型具有重要的理论与工程意义。

为了弥补传统分析方法处理函数型数据时的局限性，笔者在可拓评价模型的基础上引入函数型数据分析(functional data analysis，FDA)理论[10]，其主要思想是用样本数据拟合后的函数替代原始数据进行统计分析，从而可以进一步利用函数是否连续、可导等性质做更深入的研究。针对函数型数据的研究，国内外学者在生物科学、生态环境及经济社会等领域已取得了一些成果，主要集中在数据处理[11-12]、聚类分析[13]、主成分分析[14]等方面。在评价模型方面，相关学者也进行了部分研究。Yan等[15]将FDA与可变模糊集结合提出了一种动态可变模糊集评价模型；Li等[16]将FDA理论与模糊物元理论结合，提出了D-FME模型用以进行水质评价；苏为华等[17]在经济管理与决策中提出了一种基于函数型数据的综合评价方法，并针对其特点提出了一种新的确定权重系数的“全局”拉开档次法。大坝渗流性态评价是一个复杂的矛盾问题，其指标具有多样、复杂、相关、不确定以及可转化等特点。可拓学是由我国学者蔡文于1983年创立的一门学科，其通过描述事物的可变性，将定性描述转变为定量描述，并通过建立多指标的评估模型完整评价事物。可拓评价模型在处理复杂矛盾问题中存在一定的优势，已初步应用于大坝渗流安全综合评价，并取得了不错的效果[18]。综上所述，以上基于FDA理论的方法并不能直接应用在大坝渗流安全评价中，已有研究未能建立体现指标变化趋势的综合指标体系，也未能考虑综合得分对不同时间不同的重视程度。

笔者将FDA理论引入渗流安全评价领域，提出一种基于FDA的大坝渗流安全动态可拓评价模型，利用我国一混凝土重力坝的蓄水阶段某个月的渗流安全监测数据进行分析，并与其他评价方法评价结果进行对比证明该方法的有效性和优越性。

1 基于FDA的动态可拓评价模型

大坝渗流安全监测采样数据是由n个指标(x1,x2,…,xn)按时间(t1,t2,…,tm)收集在指标xi下的原始数据构成的时序立体数据表，由于影响大坝渗流安全的各指标的量纲不同，指标之间不具有可比性，为此采用线性无量纲法对各指标量纲进行归一化处理。通过构造综合评价模型得到被评价对象在整个时间域上的综合评价值，建立如下动态评价模型：

(1)

式中：Q(t)——时间t的渗流安全综合评价指标；t1——评价时段的起始时刻；τ(t)——时间权重函数，时间权重用于体现不同时间t评价信息的重要性；αi——第i个指标的权重系数；Si(t)——根据关联函数矩阵计算得的第i个指标得分。

1.1 渗流安全综合评价指标体系

大坝坝体及基础受周围环境因素变化的作用，其渗流性能对这些作用做出不同的反应[19-20]，就监测建筑物及基础的性状而论，将视原因量(由于其变化导致建筑物及基础内部的变化)与效应量(构成建筑物及基础对原因量的变化产生的反应)两类不同的物理量而定。一般起决定性的原因量有水位(包括上、下游的水位)及温度，表征渗流性态变化的效应量有渗压和渗流量，渗流安全监测由此建立了基础指标体系。事实上，基础指标都是随着时间的推移不断变化的，两类物理量随时间的变化程度可以从相关关系中评价时变的原因量与效应量对整体安全的影响[21]。FDA理论的引入实现了基础指标变化趋势及指标间相关关系的定量化分析，进而可以得到表征渗流性态的衍生指标。本文建立的大坝渗流安全综合指标体系不仅包含温度、上游水位、下游水位、渗压、渗流量等基础指标，同时包含上游水位与渗流量相关关系、渗压变化率和渗流量变化率等衍生指标，如图1所示。

图1 大坝渗流安全综合评价指标体系Fig.1 Comprehensive evaluation index system for dam seepage safety

1.2 FDA-可拓物元模型

函数型数据分析方法首先要将散点数据拟合成光滑的函数，通过求导可以挖掘更多原始数据的变化规律。常用的平滑方法包括平滑法和插值法，当观测值准确的时候常用插值法，如果观测值有误差常使用基函数平滑法拟合函数。B样条基函数可以体现样本数据的局部特征，在函数型数据分析中已经被广泛运用，本文根据渗流安全监测数据的特点，采用三次B样条平滑法拟合函数(式(2))。

(2)

式中：xi(t)——第i个指标关于时间t的拟合函数；M——基函数个数，本文为3；ck——系数；φk(t)——基函数，本文选用B样条基函数。

结合函数型数据特点建立FDA-可拓物元模型，包含确定经典域、确定节域以及确定待评物元。

a. 确定经典域。在可拓理论中，特征量值符合要求程度存在满意区间(称为标准正域)和可接受区间(称为正域)，为考虑指标特征值对安全等级的过渡性，标准正域设置为研究对象的经典物元，依据评估指标归一化的取值范围和取值原则(数值越小对安全越有利)，将大坝渗流安全水平分为5个等级：非常安全(1级)、安全(2级)、基本安全(3级)、预警(4级)、危险(5级)，各等级标准正域为

XO={XO1,XO2,XO3,XO4,XO5}={〈0.05,0.15〉,〈0.25,0.35〉,〈0.45,0.55〉,〈0.65,0.75〉,〈0.85,0.95〉}

(3)

式中：XO——标准正域；XO1、XO2、XO3、XO4、XO5——非常安全、安全、基本安全、预警、危险安全等级的标准正域。

b. 确定节域。考虑指标特征值对等级的渐变性，将各等级正域(包含过渡域和标准域)设置为大坝渗流安全水平的节域物元。本文选取节域为

XP={XP1,XP2,XP3,XP4,XP5}={〈0,0.2〉,〈0.2,0.4〉,〈0.4,0.6〉,〈0.6,0.8〉,〈0.8,1〉}

(4)

式中：XP——节域；XP1、XP2、XP3、XP4、XP5——非常安全、安全、基本安全、预警、危险安全等级的节域。

c. 确定待评物元。对于待评价大坝渗流安全状况，待评大坝渗流安全状况所收集的评价信息用物元表示，即为待评物元(式(5))。

(5)

式中：N——待评大坝渗流安全状况；ci——影响大坝渗流安全状况的第i个指标(i=1,2,…，n)。

1.3 关联函数

可拓理论中引入可拓距和位值的概念，描述点与区间、区间与区间之间的位值关系，通过构造关联函数，确定待评对象的单指标关联度，即待评对象的第i个指标关于分类等级j的关联程度。如果研究的是在某一时刻的大坝渗流安全状况，那么xi(t)为一定值，即对应时刻评价指标的归一化值，则该时刻的单指标关联函数Kj(xi(t))可表示为

(6)

式中：ρ(xi(t),XOj)——xi(t)与经典域区间XOj的距；D(xi(t),XPj,XOj)——xi(t)与经典域区间XOj和节域区间XPj成的区间套的位值。

式(6)与经典的可拓物元模型中的单指标关联函数相同，本文研究的是某一段时间内的大坝渗流安全状况，设xi(t)为经过函数化处理的指标函数，该时段内的单指标关联函数Kj(xi(t))为

(7)

式中：t1和tm——该时段的开始时刻和结束时刻。

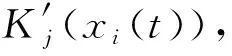
(8)

1.4 权重计算

1.4.1 时间权重的计算

动态评价问题是由时间、指标、被评价对象构成的三维综合评价问题，对于某一时刻的评价结果而言，之前不同时间数据信息的重要性对其往往不同，有效地确定时间权重是求得合理评价结果的关键。易平涛等[22]建立了一种基于离散点的时间函数来确定时间权重，本文将其改进为连续函数形式：

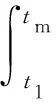
(9)

由式(9)可知，时间越接近现在时刻τ(t)越大，离现在时刻越远τ(t)越小。

1.4.2 主观权重的确定

表1 判断矩阵

1.4.3 客观权重的确定

利用熵权法确定指标的权值可有效避免人为确定权值的随意性。本文指标以连续函数表征，对基于离散型变量的信息熵进行改进得到连续型随机变量的信息熵：

(10)

式中：η——常数；pi——第i个指标处于该时间段中所占的比重，当pi=0时，则lnpi无意义，故对pi进行如下修正：

(11)

则有第i个指标的熵权为

(12)

1.4.4 组合权重的确定

求得主客观权重后，组合权重为

(13)

2 工 程 应 用

四川省某水电站拦河大坝为混凝土重力坝，最大坝高162.00 m，坝顶长度896.26 m，正常蓄水位380.00 m，水库总库容51.63亿m3，调节库容9.03亿m3，为不完全季调节水库。坝基上分布的孔隙压力计用于测量渗透压力，孔压计布置在横向排水廊道上，各监测断面孔压计一般不少于3个，取平均值作为渗透压力数据；在坝基收集井两侧、排水孔出口处，在排水廊道中设置三角形堰，测量渗流；利用水位计同步观测上游水位和下游水位，分别布置在上游水位稳定的坝段和下游坝趾处；温度监测数据取自坝区气象监测站。由于大坝处于2012年10月的第一个蓄水期，应用本文方法评价大坝渗流性态，选用该坝库蓄水期的监测数据进行短期内大坝渗流安全综合评价。

2.1 指标数据函数化

采用三次B样条平滑法拟合指标函数，拟合后的曲线如图2所示，建立渗流安全评价的待评物元。

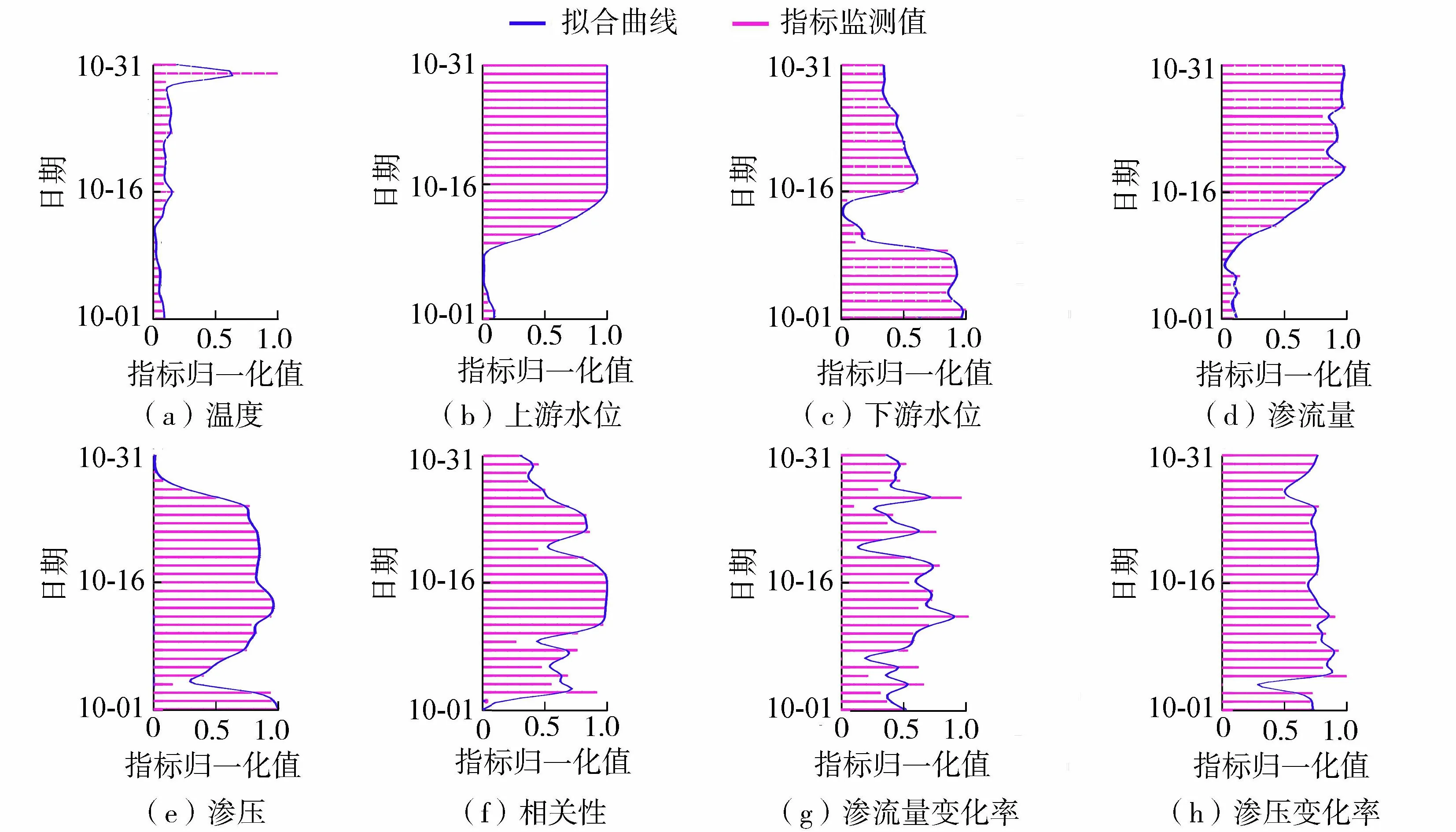
图2 2012年监测指标函数化Fig.2 Functionalization of monitoring index in 2012

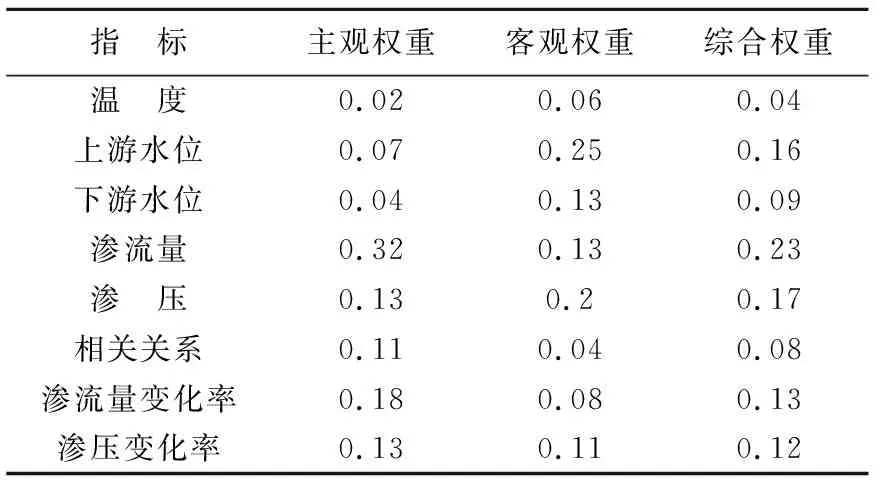
表2 基于AHP-熵权法指标权重

对基础指标进行相关性分析，计算基础指标参数间皮尔逊相关系数R的大小，其中上游水位和渗流量的皮尔逊相关系数最大为0.97，具备十分显著的相关关系，其余指标间的相关系数均小于0.65，因此选取上游水位与渗流量的皮尔逊相关系数作为衍生指标。

2.2 评价结果与讨论

根据指标值函数化结果及权重值(表2)，利用基于FDA的动态可拓评价模型进行安全等级评价计算，得出该坝坝段在2012年10月的渗流安全性态结果(图3)。由图3可知：总体趋势在2级和3级(安全和基本安全)之间变化；1—8日，渗流安全评分处在2级(安全)，但呈上升趋势，这和水库开始蓄水有关；8—27日，渗流安全评分处在3级(基本安全)，在18日达到最高分后开始呈下降趋势，因为上游水位逐渐稳定；27—31日安全评分回落到2级(安全)，虽有略微波动但呈下降趋势。因此，在该大坝关键的蓄水期，大坝渗流安全等级较低，综合评估指标值基本稳定，可基本判定该大坝在蓄水期的渗流安全状态是正常的。

图3 2012年10月大坝渗流安全评价结果Fig.3 Evaluation results of seepage safety in October 2012

选取1日、5日、10日、15日、20日、25日、30日渗流安全监测数据，利用离散可拓评价模型，分别选用基础指标和综合指标(包含衍生指标)进行安全评价计算，结果如图3(a)所示。可以得出以下结论：离散的评价结果与曲线结果接近，体现出评价结果的一致性，证明了本文方法的有效性；对比2种离散计算结果，在安全性态上升趋势下，不包含衍生指标的评价结果偏安全，在下降趋势下，不包含衍生指标的评价结果偏危险，说明考虑衍生指标会使得评价结果更加合理。在FDA-可拓评价模型中除去时间权重进行计算，结果如图3(b)所示，由图可知，考虑时间权重时评价结果变化更加平稳，减缓了指标数据波动的影响，其结果更加合理。

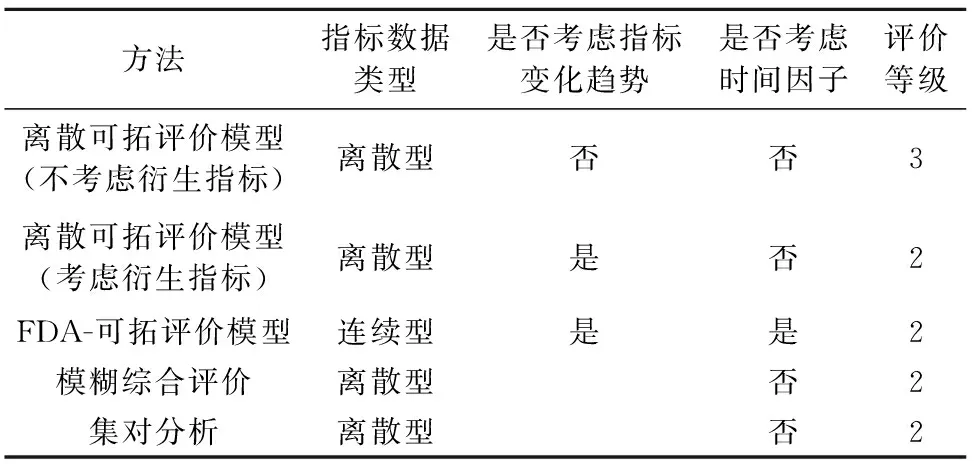
表3 不同评价方法结果对比

利用FDA方法生成30天的指标数据(包含基础指标和衍生指标)，利用模糊综合评价方法和集对分析方法进行评价结果计算，结果见表3。由表3可知：FDA-可拓评价模型与模糊评价法、集对分析法结果基本一致，并且在评价过程中采用连续型指标数据，考虑了指标的变化趋势和时间影响因子。

3 结 语

渗流性态受内外综合因素的影响，其安全状态是影响大坝安全的重要因素。本文提出了一种基于FDA的大坝渗流安全动态可拓评价模型：首先建立包含基础指标和衍生指标在内的大坝渗流安全综合指标体系；然后改进可拓评价模型，提出适用于函数型数据的物元分析及关联函数构造方法，基于FDA理论将离散指标数据转换为连续函数，分析数据的时间维度信息，同时解决监测数据时间间隔不同、数据缺失等问题；再次本研究采用AHP与熵权法相结合的主客观综合赋权法确定指标权重，并且建立时间权重体现动态评价中对不同时间的重视程度；最后，利用四川省某一混凝土重力坝的蓄水阶段10月的渗流安全监测数据进行分析，证明了该方法的有效性。