基于分散风险对多只股票组合投资策略的优化设计

张海鹏,朱家明

（1.安徽财经大学国际经济贸易学院,安徽蚌埠233030；2.安徽财经大学统计与应用数学学院,安徽蚌埠233030）

随着社会不断进步和信息技术的快速发展,经济全球化已经是世界经济发展的必然趋势,这种趋势带动了投资、金融的发展,使得金融市场间的联动效应更加紧密,这对投资者来说既是一种机遇也是一种挑战.一方面,金融产品的样式更加丰富、交易更加便捷,投资者有了更多的选择.另一方面,在金融投资便捷的同时,也可能会引发极端的风险事件.例如2008 年的金融危机席卷了全球,给散户投资者带来了巨大的损失,因此研究投资策略很有必要.董竹等[1]使用五种均线检验市场存在惯性,证明了择时交易策略能够降低风险、有效止损；黄金波等[2]扩展了经典下偏距的概念,给出了上偏距的定义,从而构建了增强指数模型,实现了稳健超额收益的目标；杨兴雨等[3]提出了一种带边信息的在线投资组合指数梯度策略并使用了实际股票数据进行了测试；徐景昭等[4]基于多因子模型进行了量化选股研究.在前人研究的基础上,我们结合了降低风险的思想并基于因子分析、马科维茨投资组合理论和理想解法设计了一套多只股票组合投资的量化策略.

1 投资目标

1.1 资产配置

资产配置是指根据投资需求将投资资金在不同资产类别之间进行分配,即“不把鸡蛋放在同一个篮子里”.其分散风险的主要方法是将国债、基金、股票、期货、外汇等多种风险各不相同的金融产品进行组合投资,在保证不损失本金的条件下获得更大的收益[5-6].例如,风险厌恶者可以更多得投资国债和保本型基金,风险偏好者则可以更多得投资股票、期权、外汇以获得更高的利益.

1.2 投资目标

这里的投资策略设计只关于股票投资市场,暂不纳入其他金融工具,尽管如此,不同股票的投资风险也有较大差异,投资时进行资产配置仍然很有必要.本策略的目标是为股票投资者设计一套符合其风险偏好的股票投资策略,在保住本金的条件下获得超额收益.

1.3 研究过程

投资策略设计分为四个阶段,分别为：选股、精选股票、模拟股票组合、求得最优股票组合,详情见图1.

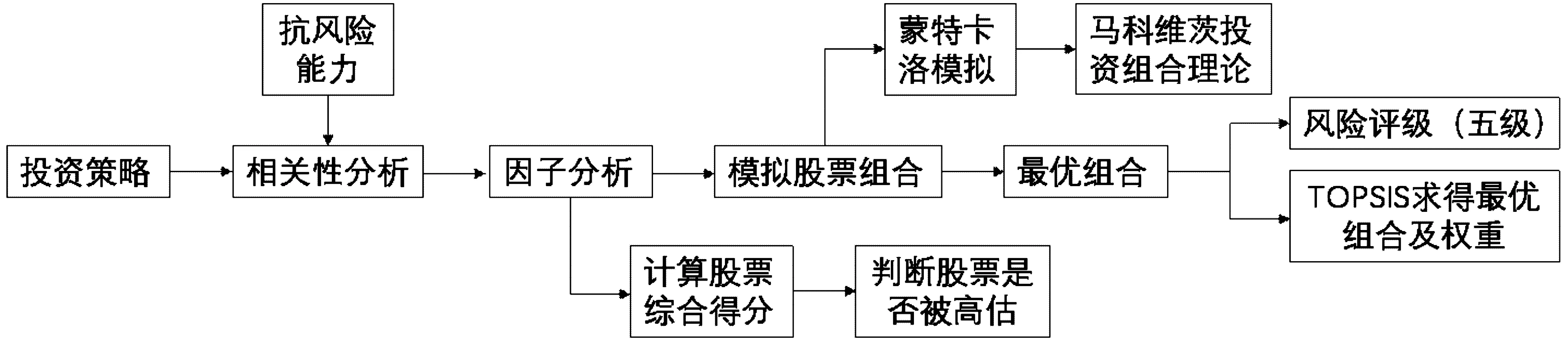
图1 研究过程Fig.1 Research process

2 基于分散风险的选股策略

2.1 对百分比变化率的分析

计算股票的相关系数一般采用股票的收盘价或者股票收盘价的百分比变化率为变量进行计算.由于有些上市公司的股票价格差异较大,而投资者的投资金额是一定的,采用股票的收盘价进行计算并不合适.例如,A 公司股票每股1 000 元,B 公司股票每股1 元,某投资者使用资金2 万元投资股票,1 万元够买A 公司股票10 股,剩下1 万元购买B 公司股票10 000 股.假设A 股上涨10 元,上涨百分比为1%,获益100 元；B 股上涨0.5 元,上涨百分比50%,获益5 000 元.投资者在意的是自己获益多少,而不是表面上股票价格上涨多少,所以在这里使用股票收盘价百分比变化率为变量计算皮尔森相关系数更加合适.

2.2 沪深300 股票相关性研究

2.2.1 沪深300 股票相关性计算 利用Python 从tushare 获得2018 年沪深300 股票的收盘价, 并储存为csv 文件,打开文件观察发现有极少数数据缺失,予以删除.部分数据见表1.

表1 沪深300 收盘价表Tab.1 The closing price of CSI 300 %

股票收盘价的百分比变化率计算公式为

利用皮尔森相关系数的计算公式可计算得到沪深300 股票百分比变化率的相关性矩阵见表2.

表2 沪深300 股票相关系数表Tab.2 Table of csi 300 stock correlation

2.2.2 沪深300 股票相关性分析 表2 是300 行300 列的数据, 从表中可以看出只有极少数股票间的相关系数小于0,由于数据量较大,不能够直观得看出沪深300 股票间相关性的总体规律.利用Python 绘制沪深300 股票相关性系数的heatmap 热力图见图2.

图2 沪深300 股票相关性热力图和部分股票的放大图Fig.2 CSI 300 stock correlation thermal chart（left）and zoomed-in diagram of some stocks（right）

颜色越深的格子表示对应的两只股票的相关性越接近1（极少数股票之间呈负相关,热力图中90 000个点只有1 041 个点代表的相关系数小于0）,即两只股票收盘价格百分比率的正相关性越强；颜色越浅的格子表明对应的两只股票的相关性越接近0.从图2 中可以看出沪深300 股票中相关性较弱的股票组合比较多.正相关性较强意味着股票组合中每支股票的收盘价百分比率同增同减,即失去了股票组合降低风险的功能.所以我们初步选取两两间相关性都较弱的股票进入股票池,这样能够增加股票池中股票组合的抗风险能力.

2.3 初步建立股票池

根据自己的股票市场投资经验,结合宏观经济、公司基本面数据、行业情况等初步选出大量自己心仪的股票放进股票池.由于文章篇幅的原因,这里不介绍怎样选择自己心仪的股票,而是直接从表2 中随机筛选出一个12 只股票的组合,筛选条件为两两间的相关系数都小于0.2 但大于0.

3 投资价值因子分析模型

3.1 样本选择

样本数据选择截止于2019 年1 月1 日,数据来源是resset 锐思数据库.以筛选出的12 只股票为研究对象,其中5 家在上海交易所上市,分别是华能水电、永泰能源、中国动力、山东黄金和长江电力,7 家在深圳交易所上市,分别是云南白药、万丰奥威、上海莱士、延安必康、康得新巨人网络和光启技术.

3.2 指标选取和有效性检验

3.2.1 指标选取 阅读大量文献,结合相关专业知识和当下股票市场行情,选择多因子量化投资中的12个常见因子作为分析数据,并将它们划分为价值因子、成长因子、品质因子、动量因子四个板块；其中价值因子有市盈率（PE）、市净率（PB）和市销率（PS）,成长因子有每股收益（EPS）、摊薄后的净资产收益率（ROE）、营业收入增长率（SALEg）和净利润增长率（Nlg）,品质因子有总资产周转率（TAT）、资产负债率（DAr）和固定资产比率（FAR）,动量因子有流通股年换手率（YTO）和流通股平均日换手率（DTO）[7-8].

结合金融专业知识可以知道,价值因子能在一定程度上指导投资者在股票价格低于价值时买入,在价格高于价值时卖出以获取收益；成长因子是对公司潜力大小的度量,例如互联网类型的公司,尽管目前其盈利较低,但是其潜力巨大,有许多投资者关注着它们；品质因子反映一段时间内公司的运营状况,在很大程度上决定了公司的经营效率；技术因子是投资者进行技术面分析时需要用到的指标.

3.2.2 有效性检验 从锐思数据库获得12 个指标和年化的日收益波动率（YRo）见表3.

表3 候选的财务指标数值Tab.3 Candidate financial indicator value

用所选股票年化的日收益波动率对股票对应的检验因子进行回归分析

得到每只股票对各指标的回归系数β 和相对应的t 值见表4.

表4 所选因子的有效性检验结果Tab.4 Validity test results of selected factors

由表4 可知,价值因子中的市净率和市销率,成长因子中的资产收益率（摊薄）和营业收入增长率,品质因子中的资产负债率,动量因子中的流通股年换手率和通股平均日换手率较为有效.

3.3 基于因子模型对所选股票的投资价值分析

3.3.1 主成分分析 经过有效性检验后还剩下七个指标,分别为 PB、PS、ROE、SALEg、DAr、YTO、DTO,再加上引入的日收益波动率（YRo）,共8 个指标.运用SPSS25 对它们进行相关性分析,发现某些指标间的相关性较强,有较多的信息重叠,所以需要进行主成分分析对数据进行降维.进行主成分分析需要先对数据进行KMO 和Bartlett 检验来判断所获得的数据是否适合进行因子分析.

SPSS25 输出的KMO 检验统计量为0.643,处于0.6 到0.7 之间,勉强适合做因子分析.Bartlett 检,对应的显著性为0,小于0.05,拒绝变量间相互独立的原假设,说明数据间存在较强的相关性.综合这两点可以得出结论：这组数据适合做因子分析

3.3.2 因子分析 运用SPSS25 对数据进行因子分析[9],设置特征值大于1,采取最大方差法进行因子旋转,输出公因子方差表发现除了营业外收入增长率和资产负债率外,从其余六个指标中提取的信息率都大于70%,即提取出的公因子很好得解释了这些指标；输出总方差解释表发现第一个公因子占所有因子总方差的30.149%,第二个公因子占所有因子总方差的23.765%,第三个公因子占所有因子总方差的18.753%,提出的公因子方差总贡献率达到72.667%,说明这三个公因子能够代表原来八个指标72.667%的信息,即这三个公因子能够很好得描述股票的投资价值.

3.3.3 所选股票的投资价值评价 利用SPSS25 直接输出每只股票各主成分的得分情况,结果见表5 每只股票各因子得分表.

表5 每只股票各因子得分Tab.5 The score of each stock in each factor

从表5 中可以看出,每只股票的综合得分由三个主成分共同决定,单独以某一个主成分为标准判断股票投资价值的高低显然是不合适的.我们使用一个主成分的特征值占三个主成分特征值之和的比例代表权重得到股票的综合得分公式

式（1）中：λ1、λ2和 λ3为 3 个主成分的特征值,分别为 2.973、1.791 和 1.049,可由总方差解释表获得.所以每只股票的综合得分公式

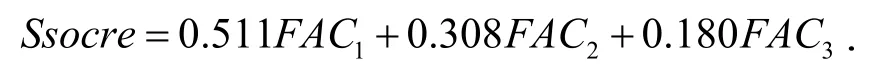
根据此公式计算得到股票的综合得分见表6.

表6 各股票的综合得分Tab.6 A composite score for each stock

表6 中的综合得分越高越好,按分值由高到低进行排序,其排名代表股票投资价值的高低；而市盈率越低投资价值越高,按市盈率从低到高进行排序（负数排最后）,其排名代表股票在当年被投资者认可的价值大小.前者大于后者,说明该股票的投资价值被高估；前者小于后者,说明该股票的投资价值被低估.

结合所选股票的排名情况可以看出,云南白药、延安必康、巨人网络、山东黄金的投资价值被低估,投资者将来一段时间内可以更多得关注这些股票；万丰奥威、康得新、华能水电、中国动力、长江电力的投资价值被高估,投资者对这些股票进行投资时应该更加谨慎；光启技术、永泰能源和上海莱士股票的投资价值没有被高估也没有被低估.

4 建立投资组合模型

4.1 马科维茨投资组合理论的主要内容

投资组合理论是指若干种证券组成的投资组合,其收益是这些证券收益的加权平均数,但是其风险不是这些证券风险的加权平均风险,投资组合能降低非系统性风险.

以期望收益E 来衡量证券收益,以收益的方差σ2表示投资风险.资产组合的总收益用各个资产预期收益的加权平均值表示,组合资产的风险用收益的方差或标准差表示,则马克维茨优化模型为

式（2）、式（3）中：E（rp）表示组合收益,ri、rj表示第 i 种、第 j 种资产的收益,wi、wj表示资产 i 和资产 j在组合中的权重,σ2（rp）表示组合收益的方差即组合的总体风险,cov（ri,rj）表示两种资产之间的协方差.此模型的经济意义是：投资者先确定一个预期收益率,在投资组合收益方差最小即风险最小的条件下通过确定的收益率获得股票组合中各只股票的权重.不同的预期收益率对应着不同的股票组合及其收益的方差,预期收益率和方差构成的曲线就是马科维茨有效前沿曲线[7].

4.2 求得所选股票的权重

经过前面的分析,初步建立的股票池中的云南白药、延安必康、巨人网络、山东黄金四只股票具有较高的投资价值（也可以直接使用你想购买的股票）.接下来我们结合蒙特卡洛模拟方法,运用马科维茨投资组合理论并利用Python 模拟出1 000 组由这四只股票组成的股票组合,并储存每个股票组合所对应的组合收益、风险及其每只股票的权重.利用Python 给出有效前沿上股票组合的风险收益和权重表见表7,画出马科维茨有效前沿曲线见图6.

表7 有效前沿上股票组合的风险收益和权重Tab.7 Risk-return and weight of stock portfolio on effective frontier %

图3 股票组合的有效前沿曲线Fig.3 The effective frontier curve of stock portfolio

在图3 中,每一个点对应一个股票组合,其横坐标是风险,纵坐标是收益.全部股票组合在图中形成一个二次曲线区域,其中曲线部分是马科维茨有效前沿曲线.通过对图3 进行分析可以发现.

（1）A 点处的投资组合风险最小,为10.23%,其收益率为23.11%.风险极度厌恶者可以选择这个股票组合,其预期收益率最少有12.88%.

（2）控制股票组合的风险不变时,投资者都会选择收益率最高的股票组合.每一个风险水平对应的收益率最高的股票组合构成了马科维茨有效前沿曲线,即图6 中的曲线部分.投资者购买这部分股票组合获益最大.

（3）在投资者是风险厌恶者的假设下,投资者购买曲线部分中哪一个股票组合取决于其风险承受能力,风险承受能力越高,就会购买收益率更高的股票组合.

4.3 风险评级

投资者的风险承受能力决定了其选择有效前沿中哪部分股票组合较为合理.为了得出适合不同风险承受能力的投资者的股票组合,我们需要对风险进行评级.

从表7 中可以看出,随机模拟1 000 次获得的有效前沿有48 个股票组合（由于是随机模拟,每次运行软件曲线上的股票组合有略微差异）.我们将其按照风险大小升序排列,并分为5 组,前3 组每组10 个股票组合,后两组每组9 个股票组合；5 组的风险评级分别为A、B、C、D、E,A 级风险最高,E 级风险最低.详情见表8.

表8 股票组合风险评级Tab.8 Portfolio risk rating

投资者需要根据自己的风险承受能力和表8 中的风险评级确定适合自己的风险等级,然后在相应风险等级的股票组合中选择适合自己的投资组合.

5 基于TOPSIS 法求各风险等级最优股票组合

5.1 TOPSIS 法原理

TOPSIS 法根据有限个评价对象与理想化目标的接近程度进行排序的方法,是在现有的对象中进行相对优劣的评价.其基本原理,是通过检测评价对象与最优解、最劣解的距离来进行排序,若评价对象最靠近最优解同时又最远离最劣解,则为最优；否则不为最优.具体的计算过程见司守奎的《数学建模算法与引用（第二版）》[10-11].

5.2 求解结果及其分析

计算理想解时认为收益率和风险同样重要,即它们的权重均为0.5.利用MATLAB 设计算法求出结果并整理成表,见表9.

表9 综合指标值及其排名Tab.9 Composite index value and its ranking

从表9 可以得到各个风险等级中的最优股票组合,结合表7 有效前沿上股票组合的风险收益和权重表可以整理得到各个风险等级的最优股票组合及其权重,详细信息见表10.

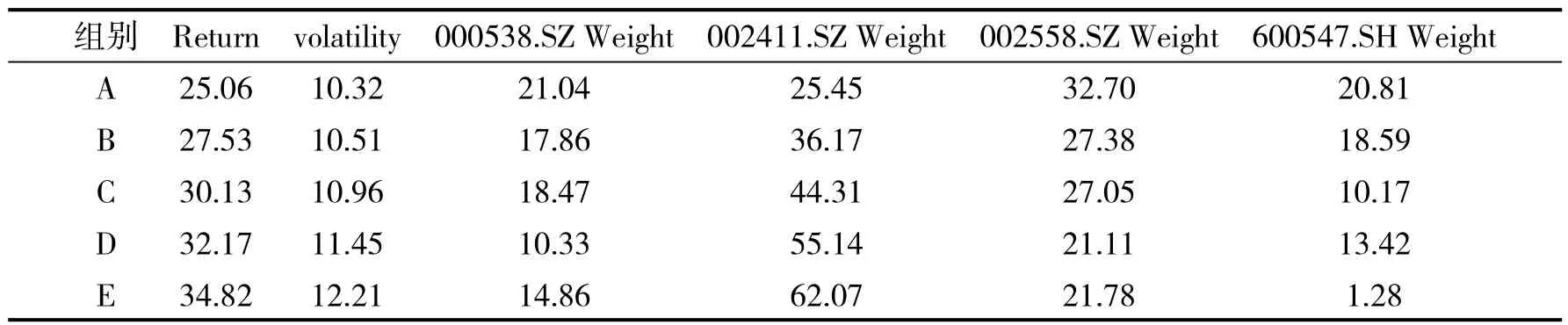
表10 各个风险等级的最优股票组合及其权重Tab.10 The optimal stock portfolio of each risk level and its weight %

分析上表中各个风险等级的最优股票组合可以发现：

（1）随着风险的增加,股票组合的收益率也在增加.

（2）随着风险的不断增加,002411.SZ（延安必康）的权重在不断增加,说明这只股票的投资价值比较大；600547.SH（山东黄金）所占权重不断下降且下降速度较快,说明这只股票的投资价值比较低.

（3）风险等级为A（风险最低）时,四支股票所占权重分配比较均匀,说明这个股票组合非系统性风险比较低,也验证了前文分析的理论：相关性低且权重分配较均匀的股票抗风险能力较强.

6 总结及建议

6.1 研究成果总结

首先利用皮尔森相关性结合分散风险和相关投资学的知识介绍了如何挑选抗风险能力强的股票组合,构建股票池；然后运用因子分析方法,构建了一套计算股票综合得分和判断股票投资价值是否被高度的综合体系,进一步筛选股票池中的股票；接着运用马科维茨投资组合理论、蒙特卡洛模拟方法,利用Python 软件模拟出了1 000 组4 只股票的投资组合；最后基于这1 000 组股票组合,构建了一套风险评价体系（五级）,并运用TOPSIS 理想解法原理,得到了各个风险等级的最优股票组合及其权重分布.对不同风险承受能力的投资者进行投资有较强的指导意义.

6.2 对投资者的投资建议

（1）提高专业素养.纯数理方面的投资策略是投资者投资的辅助工具,投资者必须学习金融、会计方面的知识,加强对诸多概念的理解,关注国家政策的变化等.

（2）提高心理素质.股票投资对心理素质的要求比较高,投资者必须清晰得认识到自己的风险承受能力,加强对诱惑的抵御能力,不受小道消息的影响.

（3）加强行业研究.投资者不能每个行业都了解一点,而应该挑选一两个自己感兴趣的行业进行深入探究,不断学习与它们相关的知识并关注与它们相关的新闻,掌握行业的风吹草动,这样投资时才不会提心吊胆.