龙泉煤业南胶带大巷围岩控制技术研究与应用

张峥嵘

(1.吕梁职业技术学院,山西 吕梁 032300;2.吕梁经济技术开发区管委会,山西 吕梁 032300)

1 工程概况

太原煤炭气化集团龙泉煤业南胶带大巷主要为矿井提供运输、行人等服务,巷道长度2 154.6 m。巷道顶板较破碎,节理裂隙发育,倾角较大,约12°～13°。巷道底板下有厚度为4.94～5.88 m的煤层,倾角多为5°～10°。该区域4#煤层顶板岩层主要由砂质泥岩及粉砂岩组成,局部为中细粒砂岩,岩性较硬,属中—难冒落顶板。南胶带大巷掘进断面为矩形,掘进宽度5.7 m,高度3.75 m,断面面积21.38 m2。为保障南胶带大巷围岩的稳定,对巷道围岩控制技术进行分析。

2 围岩控制技术

2.1 锚杆(索)支护理论

1)锚杆支护原理。现欲采用锚索-锚杆联合加固方法对其进行支护,从而形成理论上的“双重组合加固拱”。这种支护不但对破碎围岩有控制的作用,还有效限制了围岩的弹塑性变形，使巷道围岩的变形大幅减小,最大程度地保证巷道断面的充分利用,展现其优越的支护能力。

均匀压缩带(拱)理论认为,锚杆对巷道围岩产生作用时,每一根锚杆的两头会形成锥形的筒状压缩区。如果锚杆之间的间距足够小,排列成锚杆群,那么就会在巷道围岩中形成均匀的、相互交错重叠的应力支撑带,就是组合拱或压缩拱[1-2]。这种组合拱既承载着上部破碎围岩的径向压力,又承载着该组合拱内部岩层产生的径向及切向应力,整体岩层形成了三向应力状态,使其围岩强度提高,支撑能力也随之加大,如图1所示。

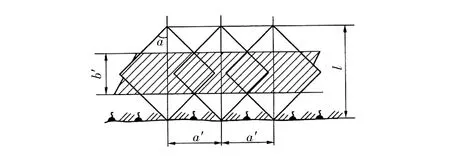
(a) 锚固体的均匀压缩带

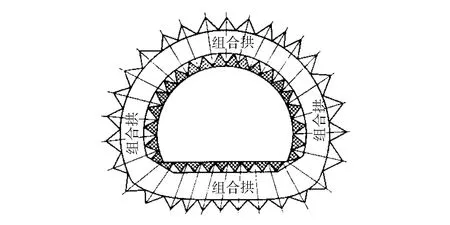
(b) 锚杆支护的均匀压缩拱图1 锚杆支护均匀压缩带(拱)支护理论示意图Fig.1 Theoretical schematic of even compression belt (arch) of bolt support

按组合拱理论,锚杆的间距与压缩拱厚度的关系可由下式确定[3]:

(1)

式中:b′为组合拱或压缩拱的厚度,m;l为锚杆有效长度,m;α为锚杆在破裂岩体中的控制角,(°);a′为锚杆的间排距,m。

锚杆的长度用下式确定:

l=N(1.5+B/10) .

(2)

式中:B为巷道跨度,5.7 m;N为围岩稳定性影响系数,取1.1。

计算得锚杆长度l=2.27 m,再补充上一定的富裕值,最终将锚杆的支护长度定为2.4 m。

2)预应力锚索支护原理。预应力锚索不但具备预应力锚杆所拥有的对围岩的加固能力,且因其长度特点,将其长锚索的锚头锚入深部稳定岩层可以达到限制围岩变形的效果。由于锚索长度较长,故其锚头经过围岩松动区和塑性变形区深入到原岩应力区进行锚固,根基就比锚杆深许多[4-5]。

生产锚索的材料具有高强度性,包括高强钢丝、钢绞线或钢筋,最大抗张拉荷载能达到1 000～6 000 kN,煤矿常用的锚索也在200 kN以上。在其产生的预应力作用下,松散围岩会出现弹性收缩,从而形成一个自我承载区域,提高了围岩的整体承载能力,三维应力呈平衡状态,通过围岩的原有承载能力及预应力锚索的联合力保障围岩的稳定。每根锚索都可以看作一个铰支点,把巷道顶板的整体承载分为一个个小跨梁(如图2所示),把顶板的整体载荷均匀分布到每个绞支点上,这样就提高了组合梁的整体受力极限,维护了巷道的稳固[6]。

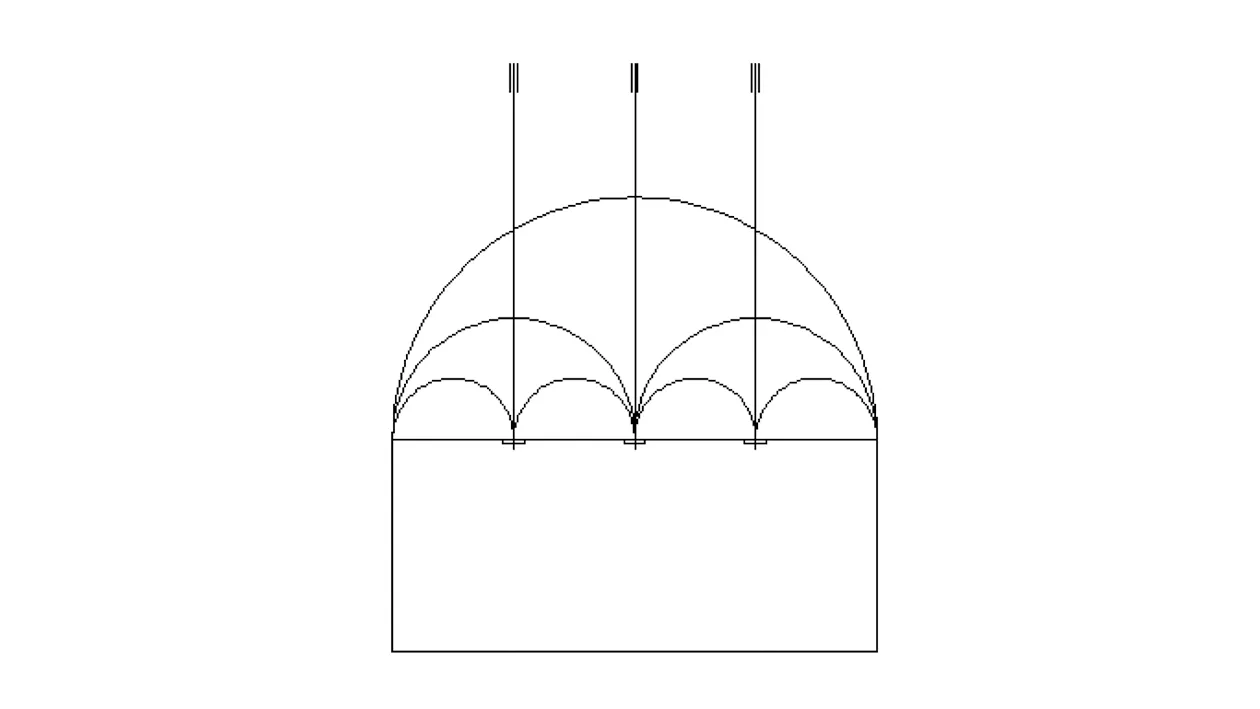
图2 锚索减跨作用原理示意图Fig.2 Principle of span reduction of anchor cables

2.2 支护方案

分析南胶带大巷的地质条件及对锚杆(索)支护原理的认知,采取如下具体支护方案。

1)顶板支护方案。锚杆采用MSGLW-500型。杆身为Φ22-M24-2400 mm左旋无纵肋螺纹钢锚杆;钻头直径为30 mm,用端头锚固方式进行锚固;两支树脂锚药卷,规格分别为MSCK2335和MSCK2360;间排距850 mm×1 000 mm;锚杆梯子梁所用材料为Φ14 mm的钢筋,长5 300 mm,宽100 mm;共布 7孔,孔间距850 mm。

锚索由Φ21.8 mm×7 000 mm预应力钢绞线配树脂锚固剂构成。利用端头锚固方式进行锚固,共三支树脂锚药卷,包括一支MSCK2335和两支MSCK2360锚固剂,配套直径为30 mm的钻头;“二三五花”布置,两根间排距为2 300 mm×2 000 mm,三根间排距为1 850 mm×2 000 mm;锚索托盘采用300 mm×300 mm×16 mm高强度可调心托板、半圆球型垫及配套锁具。

2)巷帮支护方案。锚杆型号、钻头参数和锚固方式等都与顶板支护的锚杆布设相同,但其间排距设为900 mm×1 000 mm。

锚杆配件:半圆球型垫、高强锚杆螺母及托盘同顶板材料一致,并配合W钢护板(规格400 mm×280 mm×3 mm)进行联合支护。网片规格:网孔采用50 mm×50 mm规格,网片采用3 300 mm×1 200 mm规格,连接用的双丝双股扭结至少达到3圈,联网间距至少每米10扣以上。

巷道锚杆的具体安装角度、位置及各项支护参数如图3所示。

2.3 数值模拟验证

采用FLAC3D数值模拟软件建立模型核验该支护方案的可行性。数值模型的尺寸为200 m×80 m×60 m(高),按照建模初始应力平衡巷道开挖支护数值模拟结果进行分析研究,数值模拟结果如图4所示。

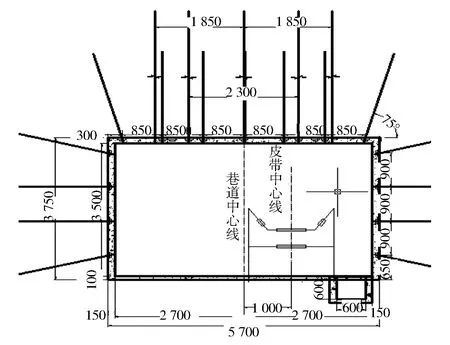
图3 南胶带大巷优化支护断面图Fig.3 Cross-section view of Optimal support in south-wing belt conveyor transportation roadway

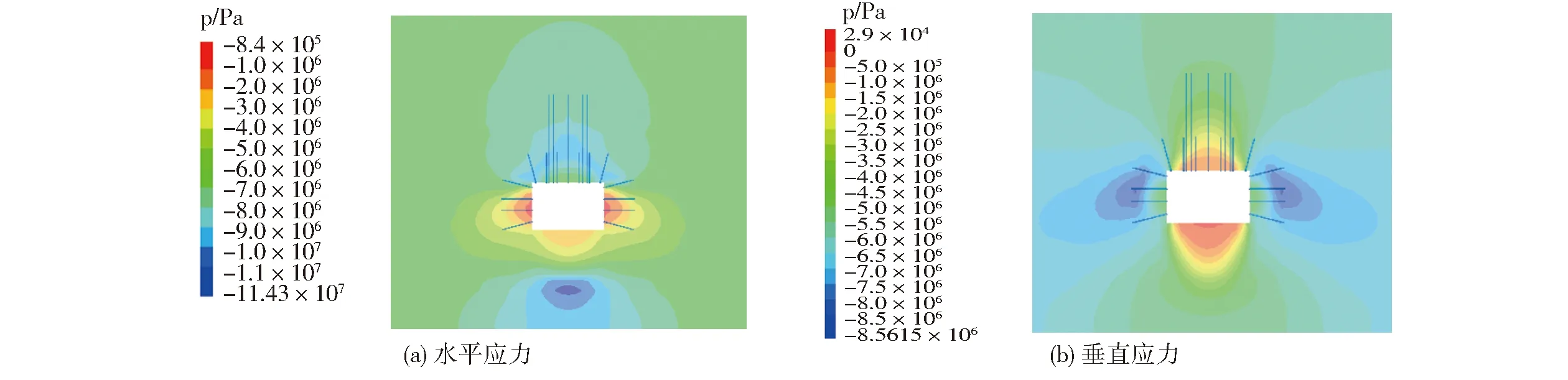
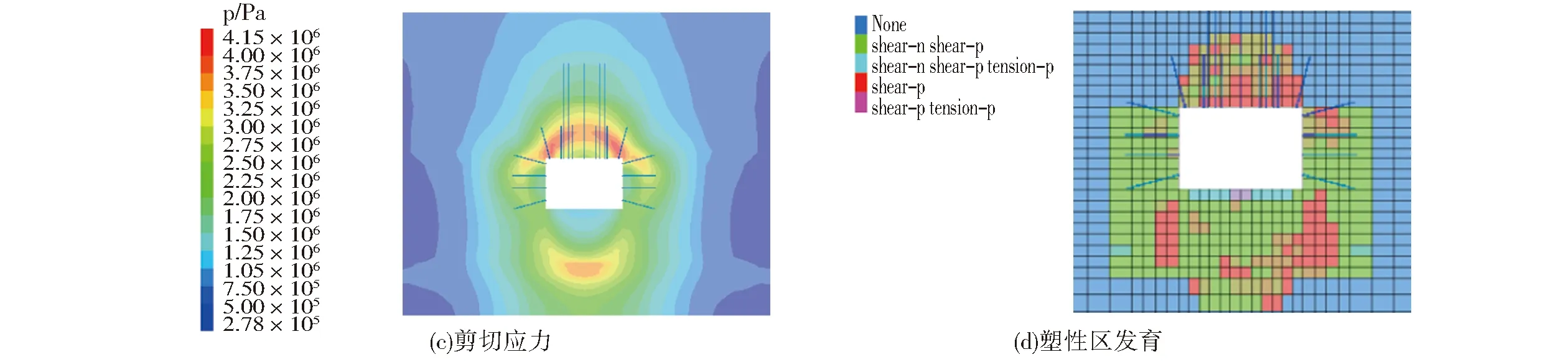
图4 数值模拟结果示意图Fig.4 Numerical simulation results

由图4可知,巷道掘进过程中,两巷帮围岩的垂直应力集中区域(b)不是很大,其峰值达到了8.56 MPa;巷道顶底板部分区域出现一块比较明显的剪切应力区(c),峰值可达4.15 MPa;巷道的顶底板同时出现了小部分的的水平应力(a),峰值达到11.43 MPa。基于以上分析可知,巷道顶板及两帮塑形区发育程度较小,锚杆(索)锚固岩层未出现塑形破坏。另外巷道在该种支护方案下,围岩水平应力、剪切应力及垂直应力分布均匀,巷道两帮水平应力集中程度较小。

综合上述数值模拟分析结果,在该支护方案下，围岩中的应力分布均匀,塑性区发育也处于合理范围内,支护方案能够保障巷道围岩的稳定。

3 效果分析

3.1 测站布置

为验证支护方案的可行性及支护效果,在滞后南胶带大巷掘进头8 m的位置处安置矿压监测站,主要测量巷道表面的变形量和锚杆(索)的受力情况。利用十字布点法测量巷道的表面移近量。安装7个锚杆测力计观测锚杆(索)受力情况,顶板锚杆测力计3个,两帮锚杆测力计各2个,分别安装在第二、三根锚杆端头处,均采用内大外小两个托板将锚杆测力计夹在中间。

3.2 巷道表面位移分析

由以上测站观测数据绘制出了巷道围岩变形量-时间的变化曲线,如图5所示。

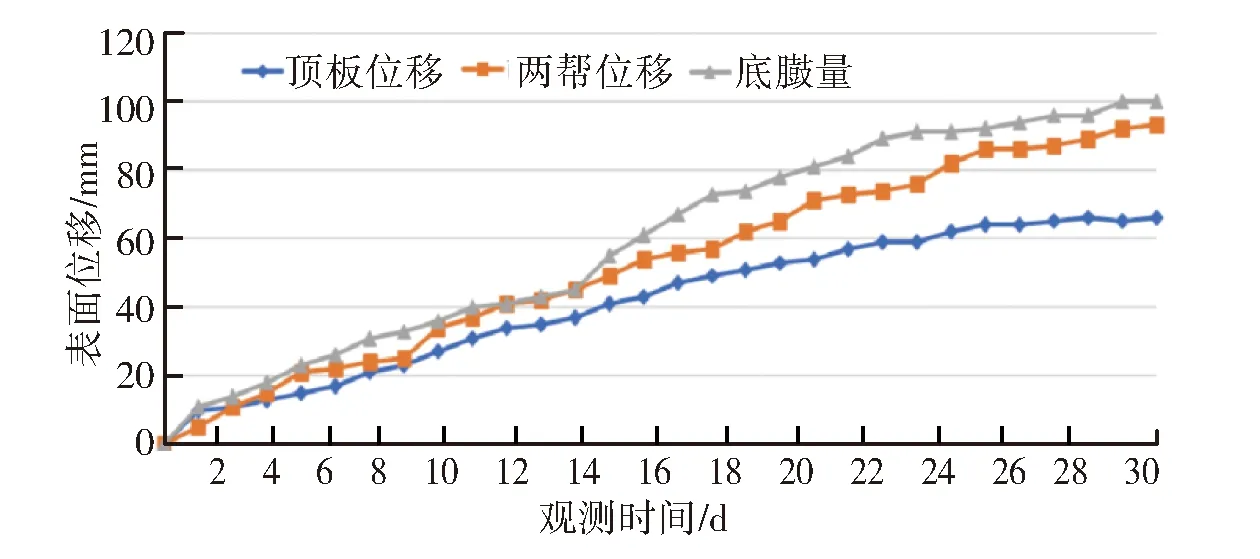
图5 巷道掘进期间围岩变形量曲线图Fig.5 Deformation curve of surrounding rock during roadway driving

分析图5可知,胶带顺槽掘进期间,巷道围岩的变形量随着距掘进迎头距离的增大而逐渐增大。其中,围岩的变形主要发生在掘进工作面后方0～40 m;当监测断面滞后掘进工作面40 m后,围岩变形速率大幅减小,变形区域逐渐稳定。通过对比顶底板移近量和两帮移近量的参数可知,巷道围岩两帮的移近量相对较大。当巷道围岩处于稳定状态后,两帮和顶底板移近量的峰值分别达到了22 mm及86 mm,故掘进期间巷道围岩移近量处于可控范围内,基本保持稳定状态。所以,南胶带大巷采用的优化支护方案是符合工程要求的合理方案。

3.3 锚杆索受力情况

通过巷道掘进时巷帮锚杆和顶板锚索的受力状态，以及锚杆(索)测力计测得的监测数据,绘制了帮部锚杆及顶板锚索随时间变化的受力变化曲线,如图6所示。

分析图6(a)可知,巷道掘进期间,巷道帮部锚杆测力计G1整体呈增长的趋势,受力大,峰值达109.02 kN(约为屈服载荷的57.38%),锚杆受力正常,无锚杆失效和拉脱的现象出现,仍在稳定承载范围内;分析图6(b)可知,锚索预应力173.9 kN,峰值203.04 kN (约为屈服载荷的40.61%),锚索受力也处于合理范围内,无失效现象出现。

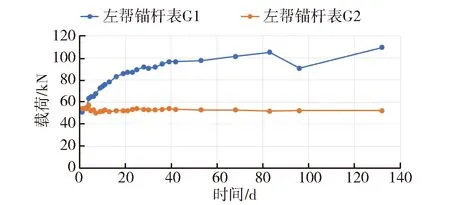
(a) 帮部锚杆

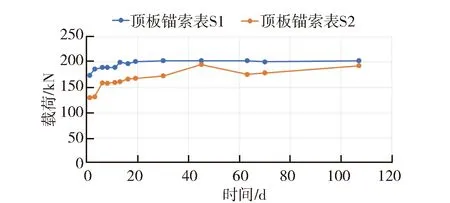
(b) 顶板锚索图6 锚杆(索)受力曲线图Fig.6 Curves of anchor (cable) stress

4 结论

根据南胶带大巷的具体地质条件,通过分析锚杆(索)的支护原理,设计巷道锚网索支护方案,并在支护方案实施后进行矿压监测。矿压监测数据的结果表明,巷道两帮和顶底板移近量的峰值分别达到了22 mm和86 mm,掘进期间的整体变形量处于合理范围内,锚杆(索)受力也正常,该方案切实保证了巷道围岩的稳定。