基于RSM-BBD的浮选金精矿碘化浸出工艺优化

康 华， 王会平， 李桂春， 徐德永， 孟 齐

(黑龙江科技大学 矿业工程学院， 哈尔滨 150022)

0 引 言

碘化法浸金因具有浸金速度快、浸出率高、药剂无毒、处理矿石类型广等优点而备受国内外研究学者关注[1-3]。俄罗斯国立贵金属勘探研究院通过配制金-碘络合物，对溶液化学性质进行研究，发现其在常温状态下的稳定性仅次于金-氰络合物[4]，说明采用碘化法对金矿石进行浸出具有可行性。李桂春等[5-6]采用碘和碘化物作为浸金试剂对金矿石进行浸金实验，碘化钾为络合剂，在碘与碘化钾摩尔比小于3∶10，pH为3～5，浸出时间4 h时，金的浸出效果最佳，且碘化浸金相较于氰化浸金的浸出时间明显缩短。Wang等[7]采用碘化法处理含铜氧化金矿石，基于成本分析法对浸金工艺进行经济可行性分析，因浸出剂价格高、杂质对金的浸出影响较大，导致该工艺的生产利润较低。李绍英等[8]对含金矿石进行碘化浸出，得出金浸出率可达88%以上，但碘和碘化物消耗量大，导致生产成本高。针对条件实验优化，多数研究采用正交实验法。庞朝霞[9]采用正交实验法对I2-KI-H2O2体系的浸金工艺条件进行优化，分析各因素对结果的影响，确定影响因素的主次关系。相较于正交实验法，响应面法用于条件优化可以更加直观和准确地呈现出各因素与响应值之间的影响变化情况，同时，可以建立预测模型，便于预测不同条件下的响应值范围。因此，笔者采用碘化法对浮选金精矿进行浸出实验，并借助响应面法对碘化浸金工艺条件进行优化，以期得出优化的工艺条件，降低浸金工艺成本，推进碘化法浸金实现工业化应用。

1 单因素实验

1.1 原料

实验所用矿样为山东招远金矿集团生产的浮选金精矿。主要元素分析结果如表1所示。

1.2 材料与仪器

试剂：碘、碘化钾均为分析纯，双氧水(分析纯不小于30.0%)，盐酸(分析纯为36.0%)，氢氧化钠，实验用水为去离子水。

仪器：XMQ-φ240 mm×90 mm锥形球磨机，DHG-9070A电热恒温鼓风干燥箱，JJ-4B六联异步电动搅拌器，STARTER2100/3Cpro pH计，岛津AA-6880原子吸收分光光度计，FA214电子天平。

1.3 方法

浸出剂配制：称取一定量的I2和KI置于烧杯中，加入一定量的去离子水，待碘单质完全溶解后视为配制完成，实验所用试剂均为即用即配。

以1 L烧杯作为反应器，根据实验条件进行加药，用搅拌器以搅拌速度500 r/min进行搅拌，同时计时完成浸出实验。实验结束后，浸出矿浆保存备用，利用原子吸收分光光度计对浸出液中的金含量进行测定，计算金浸出率。在改变单因素条件下进行金的浸出实验，得出金浸出率处于较高水平时的各因素取值范围。

1.4 结果

采用单因素实验法考察细粒比α、碘初始质量浓度ρ、碘与碘离子摩尔比n、液固比β、pH值和浸出时间t对金浸出率η的影响，实验结果如图1所示。由图1a、c可知，随着细粒比和碘与碘离子摩尔比的增加，金浸出率呈持续上升趋势，考虑到实际生产过程中的经济成本(当金浸出率呈升高趋势缓慢的情况下，应尽量减小细粒物料的占比以降低磨矿过程所产生的耗能和减少浸出药剂的用量)等因素，故选择细粒比为99.3%和碘与碘离子摩尔比为1∶6最为合适。由图1b、d、f可知，碘初始质量浓度、液固比和浸出时间对金浸出率的影响明显，随着各因素取值的不断增加，金浸出率都呈先持续升高后逐渐平缓的趋势，当ρ为6～8 g/L，β为3∶1～4∶1，t为3～4 h时为最佳范围，此时金浸出率处于较高水平，可达88%～90%，继续增加碘初始质量浓度、液固比、浸出时间，金浸出率的升高不明显。在实际生产中，碘用量和浸出时间是导致生产成本增加的主要因素，若能对其进行合理控制，对实现碘化浸金的大规模化生产具有重要的意义。由图1e可知，金浸出率随着pH的增大呈先升后降的变化趋势，当pH值在6.5～7.0范围内时，金浸出率最高可达90%左右，由于Au-I2-KI浸金体系溶液的初始pH为弱碱性至中性，即溶液环境pH值已在最佳范围内，所以，碘化法浸金过程中无需调节pH值。综上得出，α为99.3%，pH为6.5～7.0，ρ为6～8 g/L，n为1∶6，β为3∶1～4∶1，t为3～4 h，此时金浸出率达到89%左右。

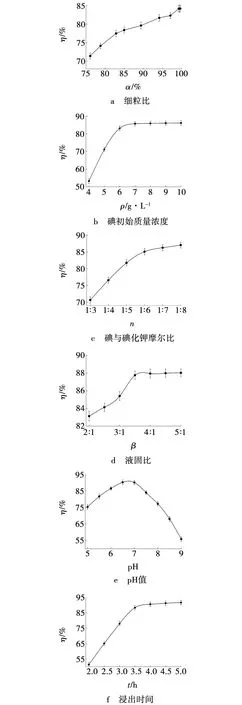
图1 单因素对金浸出率的影响Fig. 1 Influence of single factor on gold leaching rate

2 响应面法优化实验

2.1 实验设计

为了考察单个因素及其交互作用对金浸出率的影响，结合单因素实验结果，分析影响金浸出率的关键因素及交互因素，优化浸金工艺条件，实现降低生产成本、提高金浸出效率的目的。在单因素实验基础上，选取碘初始质量浓度(A)、液固比(B)、浸出时间(C)为变量因素，以金浸出率(η)为响应值，根据Design-Expert8.0.6软件[10]中Box-Behnken Design响应面法(RSM-BBD)[11]设计了3因素3水平实验(共17组)。在温度25 ℃，α为99.3%，n为1∶6，pH为6～7的条件下进行优化实验。变量因素的取值如表2所示。

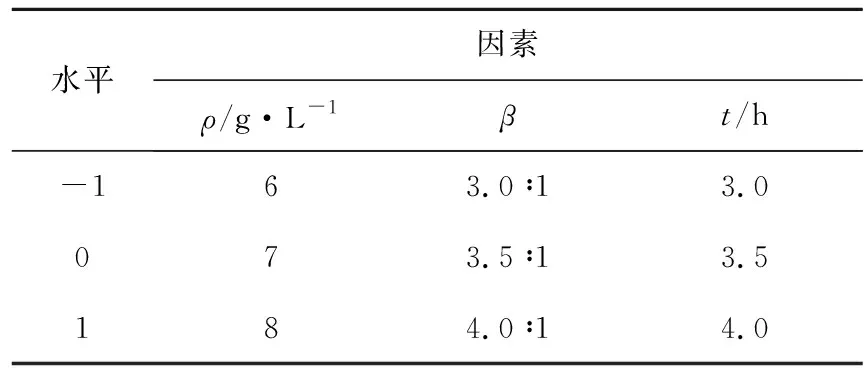
表2 响应面法分析因素与水平Table 2 Response surface analysis factors and horizontal coding

2.2 实验结果与回归分析

实验方案与结果如表3所示。根据实验结果进行回归分析，结果如表4所示。

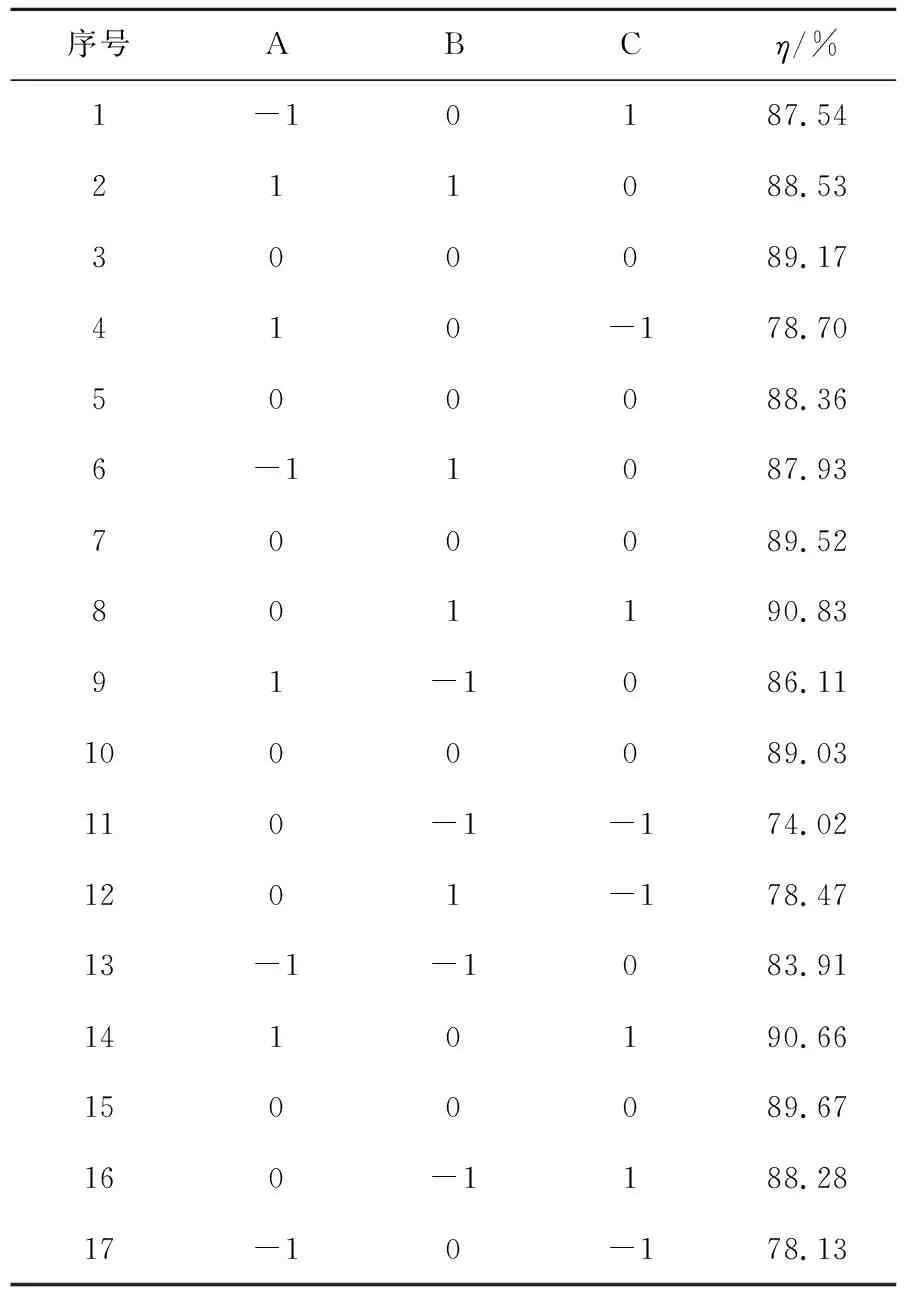
表3 响应面分析方案与实验结果Table 3 Analytical project andtest results of response surface method

由表4可知，模型F值为71.91，表明该模型的可信度极高，P值表示变量因素对响应值影响的显著性，其数值越小越显著，该模型P<0.000 1<0.05，说明模型出现信噪比错误的概率小于0.01%，即实验过程中不受失拟因素的影响[12]。

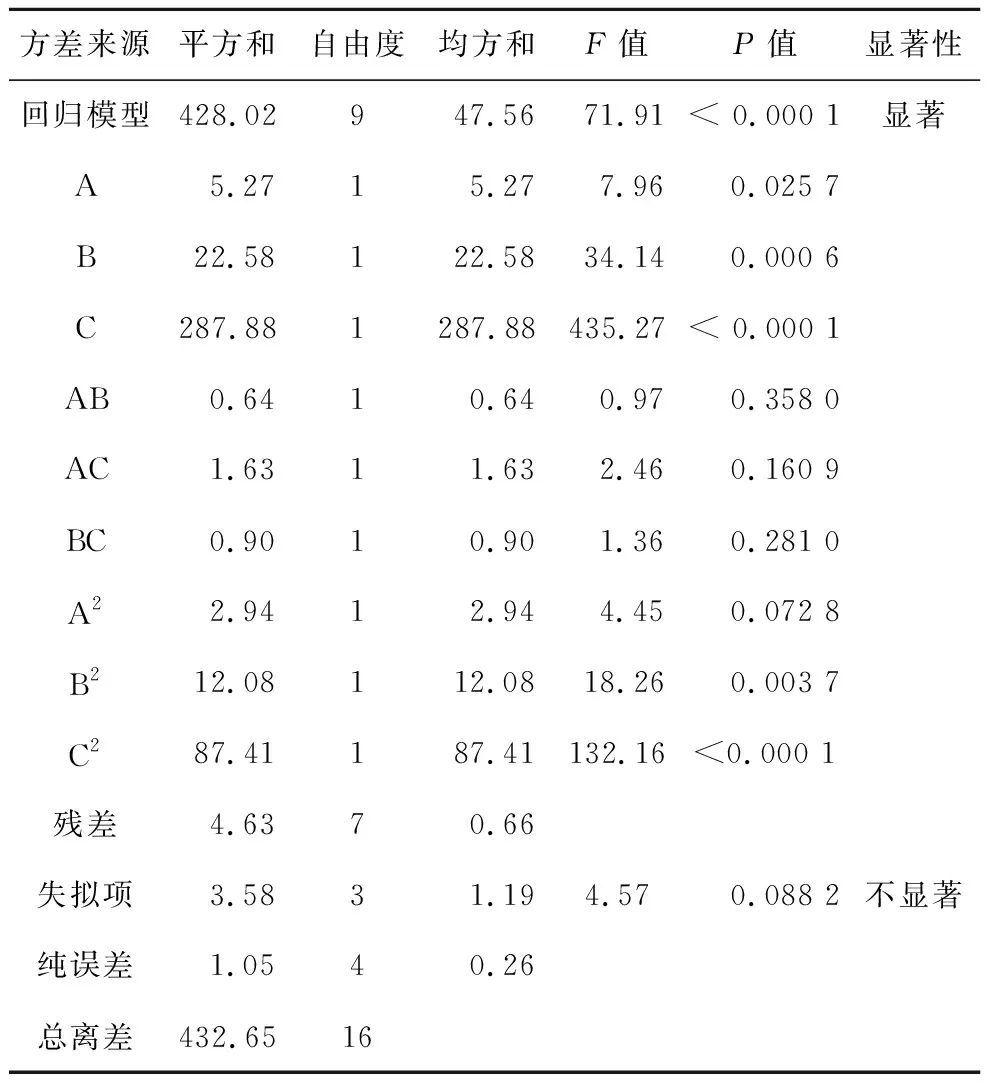
表4 回归分析结果Table 4 Regression analysis results

图2为金浸出率实际值η与预测值ηa对应关系。由图2可知，实际值的分布情况与预测值直线重合度很高，两者的拟合结果显示其相对误差小于5%，说明该响应面优化模型对金浸出率的预测准确，通过关系图可以初步预测不同浸金条件下的金浸出率。

图2 预测值与实际值关系Fig. 2 Reation of predicted value and actual value

将响应值金浸出率与3个变量因素进行回归拟合，得出金浸出率的二阶回归方程：η=89.15+0.81ρ+1.68β+6.00t-0.40ρβ+0.64ρt-0.48βt-0.84ρ2-1.69β2-4.56t2，其相关性系数R2=0.989，根据R2与1的接近程度可以判断二阶回归方程的预测可靠度，R2越接近于1，则预测可靠度越高，同时也反映出所建立的响应面优化模型的准确性越高[13]。

通过对回归方程模型进行方差分析可知，模型一次项A(P<0.05)、B(P<0.05)、C(P<0.000 1<0.05)，说明3个变量因素对金浸出率的影响显著；交互项AB(P=0.358 0)，AC(P=0.160 9)和BC(P=0.281 0)，即两因素交互作用对金浸出率有一定影响，但显著性不高；二次项A2(P=0.072 8)，影响不显著，B2(P<0.05)和C2(P<0.000 1<0.05)，影响显著。同时，根据二阶回归方程中的一次项系数绝对值的大小可以判断出各变量因素对金浸出率的影响程度，即各变量因素与金浸出率的主效应关系：浸出时间(C)>液固比(B)>碘初始质量浓度(A)。

金浸出率的响应曲面和等高线如图3所示，通过响应曲面边缘与中心点之间的坡度可以判断变量因素对金浸出率的影响程度，坡度越大，该因素对金浸出率的影响越大。等高线图中的每条等高曲线所围成的圆形的规则程度能够反映两因素的交互作用对金浸出率的影响，圆形表示影响不显著[14-15]。

由图3a可知，当碘初始质量浓度为6.8～7.8 g/L，液固比为3.4∶1～3.9∶1时，金浸出率达到最优范围。同时，由响应曲面边缘与中心点的坡度可知，两个因素对金浸出率的影响均较为显著；其等高线图(图3b)呈偏椭圆状，说明两因素的交互作用影响较显著。从图3c、d可知，碘初始质量浓度为6.90～7.90 g/L，浸出时间为3.50～3.90 h为最佳区间；等高线图呈明显的长半径与短半径比值较大的椭圆，说明两因素的交互作用影响极显著。从图3e可以看出，浸出时间对金浸出率的影响极其显著；等高线图(图3f)曲线的椭圆程度介于以上两者之间。综上所述，3个因素两两之间的交互作用依次为：AC>BC>AB。根据响应面分析结果对单因素实验进行补充和修正，使工艺条件更具合理性和适用性。

图3 金浸出率的响应曲面和等高线Fig. 3 Response surfaces and contour of gold leaching rate

2.3 工艺条件优化与验证实验

响应面优化模型得出最佳工艺条件：碘初始质量浓度7.22 g/L，液固比3.81∶1，浸出时间3.68 h。为方便实验操作，将工艺条件进行修正，得出在温度25 ℃，细粒比99.3%，pH值6～7，碘初始质量浓度7.2 g/L，n为1∶6，液固比3.8∶1，浸出时间3.7 h。在该条件下进行3次验证实验，金浸出率分别为90.81%、90.45%、91.80%，均值91.02%，与预测值91.25%非常接近，证明BBD响应面法优化碘化浸金工艺条件具有可行性。将响应面优化后工艺条件下的实验结果与相关文献[7-9]所得结果进行对比，得出碘和碘化钾用量均减少了10%～15%，浸出时间缩短了5%～10%，成本得到明显降低，表明采用响应面法优化浸金条件具有实际意义。

3 结 论

(1)3个变量因素及其两两交互作用与金浸出率的主效应关系由大到小为C、B、A，AC、BC、AB。

(2)响应面优化模型得出最佳工艺条件：碘初始质量浓度7.22 g/L，液固比3.81∶1，浸出时间3.68 h，此时金浸出率为91.25%。

(3)修正后的最佳工艺条件下，金浸出率为91.02%，与模型预测值91.25非常接近，证明该响应面优化模型用于实际应用具有可行性。