不一样的“边边角”
2020-09-22 20:56董翠花
初中生世界·八年级 2020年9期
董翠花


我们知道,在判定三角形全等的条件中,“边边角”是不能作为判定三角形全等的条件的。这是为什么呢?
如图1,在△ABC 中,以点A 为圆心,AC 长为半径画弧,与BC 相交于点D,此时△ABC 和△ABD 满足AB=AB,∠B= ∠B,AD=AC,但显然△ABC 和△ABD 不全等。
那么,两个三角形具备了“边边角”的条件,就一定不全等吗?答案是否定的。
相信同学们不难想到“HL”定理。课本中给出了证明过程。我们通过画图来直观感知。如图2,∠B=90°,AB 长度一定,以点A 为圆心,定长为半径画弧,与∠B 的另一边相交于点C,此时交点唯一。也就是说,两个三角形如果具备了“边边角”的条件且相等的角是直角,那么三角形的形状就确定了,这两个三角形就全等。
在“边边角”的条件下,如果相等的角是钝角呢?
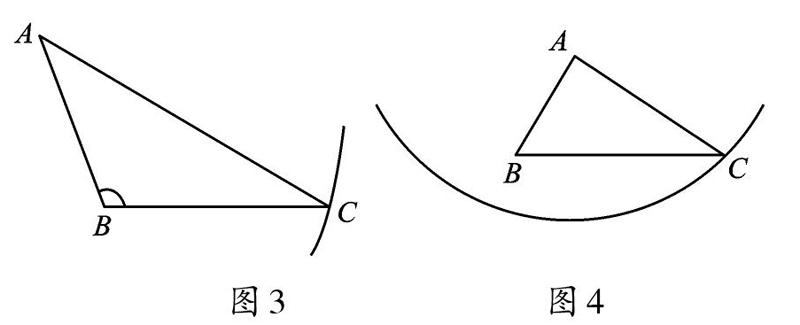
如图3,∠B>90°,AB 长度一定,以点A 为圆心,定长为半径画弧,与∠B 的另一边相交于点C,此时交点也唯一,三角形的形状也确定了。因此,如果两个三角形具备了“边边角”的条件且相等的角是钝角,那么这两个三角形全等。证明过程留给同学们。
在“边边角”的条件下,如果相等的角是锐角呢?
在图1中我们发现当∠B<90°时,以点A 为圆心,定长为半径画弧,圆弧与∠B 的另一边有两个交点C、D,满足“边边角”条件的三角形形状就不确定了。是什么因素决定了交点的个数呢?相信同学们不难发现,这跟AB、AC 的长度有关。当AB
我们回头再看一下图2和图3会发现,在这两种情形中,同样有AB≤AC。因此,我们不难得出:两个三角形在满足“边边角”的条件下,只要该角的邻边小于或等于該角的对边,这两个三角形一定全等。
猜你喜欢
初中生学习指导·提升版(2022年4期)2022-05-11
中学生数理化(高中版.高考数学)(2022年1期)2022-04-26
阅读(科学探秘)(2021年10期)2021-03-08
减速顶与调速技术(2020年1期)2020-07-27
教学月刊·小学数学(2018年1期)2018-07-16
中学生数理化·七年级数学人教版(2017年9期)2017-12-20
数学小灵通(1-2年级)(2016年10期)2016-12-13
中学生数理化·七年级数学人教版(2016年1期)2016-05-30
学苑创造·B版(2015年11期)2016-01-13
中学生数理化·七年级数学人教版(2014年1期)2014-06-20

