从现实走向教学的初中数学建模课程资源
崔竞


数学建模,就是根据实际问题来建立数学模型,对数学模型进行求解,然后根据结果去解决实际问题。在教学中,可以根据特定的研究目的,采用数学的符号和语言刻画出所研究对象的主要特征、关系,“使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程”。众所周知,“模型思想”已作为数学课程中应当注重发展的考查能力之一。数学建模活动的有效开展离不开对各种教学资源进行优化组织。下面笔者以“蚂蚁庄园中的数学”为例,谈谈如何将现实形态的数学建模课程资源变成教学形态。
一、数学建模课程资源的现实形态
数学建模课程在实施中离不开真实的问题情境,为了能激发学生的学习兴趣,问题情境应来源于学生身边,具有一定的趣味性,涉及的问题在初中生最近发展区。
蚂蚁庄园是支付宝开发的网上公益活动,网友使用支付宝付款能领取鸡饲料,喂鸡后获得的鸡蛋能进行爱心捐赠。
利用蚂蚁庄园进行数学建模的可行性分析:游戏界面上数据的动态变化,可以让学生感受到计算机编程在信息时代的重要性;作为网上公益活动,蚂蚁庄园背后的爱心捐赠可以培养学生的社会责任感;手机画面实时投屏功能可以让学生全程观看数据变化过程,让实验过程更加具有真实性;在蚂蚁庄园中涉及许多知识,比如游戏界面的艺术设计、鸡宝宝的服装设计、庄园小课堂中的中华传统文化等。
蚂蚁庄园游戏中能直接提炼的数据就有许多,例如:1.点击一次投喂,消耗180g饲料,小鸡没有吃完的情况下无法进行下次投喂;2.小鸡吃500g饲料就会产下1颗爱心鸡蛋;3.饲料不被偷吃的情况下,每3次喂养就可以产下1颗爱心鸡蛋;4.每满5颗鸡蛋就可以捐赠,且捐赠的最小单位为5颗,每捐赠5颗鸡蛋获得1点荣耀;5.蚂蚁庄园饲料盒存储量每获得5点荣耀值可多存储180g饲料;6.屏幕会实时显示剩余饲料吃完需要的时间以及外来小鸡已经进食的量。
在蚂蚁庄园游戏攻略中,我们还能获得以下信息:
1.1袋180g的饲料,自家小鸡需要5h吃完,进食速度为36g/h。2.外来小鸡来庄园蹭食时,自家小鸡进食速度不变,外来小鸡进食速度为18g/h。3.最多可以同时有两只外来小鸡一起进食。4.加速卡功能:每次用1张加速卡可以缩短自家小鸡1个小时的进食时间。
二、数学建模课程资源的教学形态
在现实形态的课程资源中,我们可以获得许多适合的信息,这些信息通过不同程度的加工,可以变成服务不同教学目的的教学内容。在数学建模教学过程中,教师在问题情境中引导学生探索得到的信息量的多少,决定了学生进行数学建模的开放程度。
(一)半开放式数学建模。
案例1. 当你进入这款互动游戏,看到图1场景,而自家粮食充足,此时多会救济朋友的小鸡。当自家小鸡在剩余进食时间3h时邀请了朋友的小鸡一起进食,那么两只鸡可以一起愉快地进食多长时间呢?
师问:解决这个问题,需要收集哪些数据?(给学生时间思考,讨论。)
讨论结束后,学生根据外来小鸡进食速度为自家小鸡一半以及“剩余饲料总量=进食速度×剩余进食时间”的模型,建立方程模型:3×36=(36+18)x,通过对模型进行求解,可知共同进食2h。点击救济卡后,屏幕显示与计算结果一致,检验模型建立有效。
评价:在半开放的数学建模教学过程中,手机、多媒体设备、蚂蚁庄园游戏成为学生看得见的课程资源,情境新颖、有趣,能培养学生观察分析、获取数据、分析数据的能力。建模结果的反馈,增加了学生解决生活实际问题的信心,让学生更加真切地感受到数学知识是有用的。
(二)开放式数学建模。
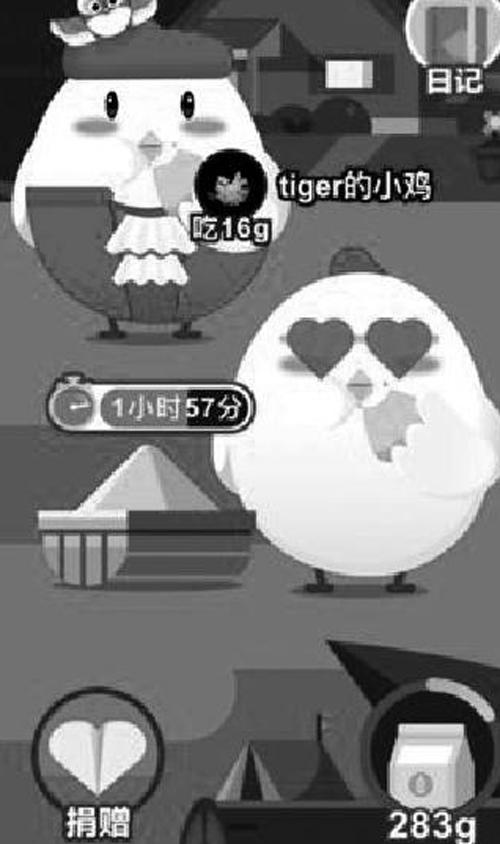
案例2. 打开蚂蚁庄园界面显示外来小鸡吃16g、剩余进食时间1小时57分,此时把外来小鸡赶走,显示剩余进食时间3h。请通过实验分析:外来小鸡进园前后,屏幕显示剩余时间之间的关系。
在开放式数学建模背景下,学生需要思考:
1. 前后剩余时间存在关系吗?
2. 在什么条件下它们之间会存在关系?
3.需要哪些信息,可以建立它们之间的关系?
4.如何通过实验的方式获得相关信息?
5.获取信息后如何建立两者之间的模型?
6.你能用数学的方式检验你的结果吗?
在师生共同讨论、总结的情况下,完成如下的数学建模过程:
1.问题分析,提出基本假设。
生活常识告诉我们,作为一款游戏,为了公平和程序的可操作性,外来小鸡到来前后的剩余时间不应该是随机的。根据“进食时间=饲料总量÷进食速度”的模型,通过饲料总量建立外来小鸡到来前后剩余时间的联系。为此,我们提出基本假设:外来小鸡到来前后剩余饲料总量保持不变,记为S;自家小鸡和外来小鸡的进食速度在游戏过程中保持勻速,分别记为V1,V2;自家小鸡进食剩余时间记为t;自家小鸡+1只外来小鸡进食剩余时间记为T1;自家小鸡+2只外来小鸡进食剩余时间记为T2。
2.实验操作,建立数学模型。
在基本假设的条件下,外来小鸡进来前后的剩余进食时间存在函数关系。通过多次实验,获得T1(T2)与t 对应的数据如表:
先将上述数据全部转换成以小时为单位,利用HP图形计算器中的双变量统计功能对变量间的函数关系进行数据拟合。拟合结果如下图所示:
从数据拟合的结果看,T1、T2与t 分别存在一次函数关系,即朋友小鸡到来前后进食剩余时间存在一次函数关系,但它们之间的函数表达式不太简洁,这是什么原因呢?教师抛出问题让学生去思考,帮助他们体会生活数学与理论数学的差别。
3.模型分析,进行数学化证明。
通过对前后进食剩余时间的数据拟合,初步感受到它们之间的一次函数关系,这种关系建立在自家小鸡和外来小鸡进食速度保持匀速的假设基础上。我们同样可以通过实验的方式检验匀速的假设是否成立。观察外来小鸡进食过程,记录如下数据:
通过上表数据,借助HP图形计算器可以推断:外来小鸡的进食速度约3min/g,若将记录时间精确到秒,会得到更加精确的外来小鸡进食速度为0.3g/min。
结果分析:从外来小鸡进食速度的实验分析上,可以发现时间的对应关系存在一定的滞后性。就外来小鸡进食看,时间变化的最小单位为分钟,进食量的最小单位为g,那么两者之间的对应关系也就存在一定的客观误差。这种误差也就造成在表1中显示的进食剩余时间存在近似计算的可能。
由生活常识可知,外来小鸡进园后,由一只自家小鸡吃变成两只小鸡一起吃,前后进食速度的变化必然引起前后剩余时间的变化。反过来,我们可以根据剩余时间的变化,来推导出前后进食速度的变化,得出自家小鸡与外来小鸡的进食速度的关系。根据前后饲料总量不变建立方程模型,计算出前后剩余时间的准确函数关系。
通过开放式数学建模活动,学生拥有解决蚂蚁庄园问题的基本活动经验。借助这些经验,学生可以继续对加速卡的功能进行分析,建立小鸡成长的快速进阶攻略。
三、反思
初中数学建模教学从贴近学生身边的问题切入,通过理论假设简化问题背景,活动设置以适合初中生能力水平为准绳,指向学生应用数学解决实际问题能力的提高。教师用数学的眼光发现生活中的数学建模资源,梳理潜在的现实形态的课程资源,是数学建模课程资源开发的起点。教师对课程资源的选取标准要适合学生最近发展区,资源的组织形式则由教学目标来决定。教学形态下的资源的呈现方式从半开放到开放的转变过程,可以让学生感受到数学建模就在我们身边,感受到学术化的数学如何从生活化的数学中抽象出来,从而提高发现身边数学的能力。
在开放式数学建模的教学中,学生自行从网络或其他社会途径中获取资源。学生参与资源开发的经历,在无形中发展了他们数据调查的能力。教学形态下的师生互动,充分突出学生的自主性,发挥学生在课程资源建设中的主导作用。
总之,在将生活中的现实资源转变成教学资源后,教师可以鼓励学生自主去解决现实问题,体会数学建模的价值。在数学建模的过程中,学生不断增强数学应用意识和应用能力,用数学的眼光看待周围的世界,懂得从数学的角度去思考问题,解决问题。

