浙东山地区域场平工程土方量优化计算方法研究

金 权 周东杰 俞梦迪 俞嘉辉

（宁波市电力设计院有限公司，浙江 宁波 315210）

0.引言

场地平整工程是指根据建设需要改造工程场地原有地貌。其中，利用地形测量结果精确计算土方量，进而平衡土方填挖量，合理选择施工人力、机械配备，是控制现场施工方案和进度的可靠依据，是影响工程项目造价和投资的关键，切实关系到工程建设各个方面。近些年来，随着经济的快速发展，城市化建设的进程也在加快。各个城市都建立起了大规模的高楼以及公路，而在这些工程的建设过程中，土方量的计算可以说是一个不可或缺的重点工作。在整个工程实施的过程中，土方工程占有者相当大的比例，而且土方量的工程最为关键的是精确度的高低，这也很大程度上会影响到整个建设工程的施工效果以及之后所带来的经济效益。因此，对于土方量的相关计算进行进一步探究显得尤为重要，我们通过对土方量计算的深入了解，进而提高工程施工过程中的精准度，从而创造更高的经济利益。

浙东区域电网工程场地大都处于丘陵地带，地形地貌较为复杂。浙江省地理特征丰富，山河湖海兼备。地势自西南向东北呈阶梯状倾斜，全省大致可以分为浙北平原、浙西丘陵、浙东沿海丘陵、中部金衢盆地、浙南山地、东南沿海平原及滨海岛屿七个地形区。全省地形起伏较大，西南多为千米以上的群山盘结，境内山地和丘陵约占70.4%，平原和盆地约占23.2%，河流和湖泊约占6.4%，故有“七山一水两分田”之说。

同时，考虑到电网工程场地的区域生态环境情况，场地平整工程中，通常采用的余土外运和购土方案的实施具有较大难度。因此，研究适用于浙东山地区域复杂地形地貌的精确土方工程量计算方法，对优化土方施工方案、缩短施工工期、降低工程造价具有显著的经济效益和重要的现实意义。

为了实现适用于浙东山地区域复杂地形地貌的土方工程量精确计算，本文在DEM 的约束不规则三角网构建算法基础上，发展出一种改进约束不规则三角构建算法，将场平工程区域边界作为约束插入初始三角网，并实现三角网约束边界自动优化，生成高精度的计算约束不规则三角模型，进而实现土方工程量的精确计算。

1.数字高程模型（DEM）方法应用于土方量计算

目前工程上计算土方量通常采用方格网法、断面法、等高线法或数字高程模型（DEM）法等。上述方法计算方法各异，在不同类型场地条件下的计算精度也存在较大差异，具有特定的适用范围。研究表明：在复杂地形地貌条件下，DEM 法相对其他方法在计算精度和稳定性上具有一定优势［1-3］。因此，本文选择在DEM 法基础上研究适用于浙东山地区域复杂地形地貌条件下的土方量精确计算方法。

数字高程模型（DEM）一类将三维地理坐标与可参数化的地形表面特征相结合的数字地图，其实质是一组定义在区域上的三维向量有限序列，因此具备计算机信息化处理的所有优势。土木工程是最早应用DEM方法的领域，Miller 等人于1958 年在道路横断面模型设计中提出DEM 概念后，这一概念被迅速推广到其他土木工程设计领域[4]。

DEM 方法随着GPS/RS/GIS 测绘技术的发展与应用，国内已经产生许多将DEM 方法应用于工程土方量计算、土地平整工程中来，在利用已有地形高程数据的情况下,实现土方量计算的自动化、可视化。茆德柱研究了不规则三角网（Triangulated Irregular Network,TIN）模型的构建方法，提出并验证了结合离散点提取、边界提取算法等的TIN 模型［5］；许多文提出了基于TIN的内插法建立DEM，并研究了土方量计算方法［6］；苗季朋对土石方工程量计算方法进行了深入研究，对影响土石方工程量计算准确度的因素进行分析，并针对性地提出了提高土石方工程量计算精度的方法[7]；李华蓉等基于TIN 模型，引入三角形微分思想，将三角形按照一定规则进行分割，通过计算微分三棱柱体积实现土石方的计算[8]；李东升等利用消费级无人机进行外业地形数据的快速采集生成的DEM，并验证了该方法计算土石挖填方的精度[9]；訾栓紧等通过控制地面分辨率和控制点布设方案对UAV-DEM 法计算土方量精度的影响进行了研究,并验证该方法的可靠性[10]；曾雨薇等将介绍并利用ArcGIS 技术将DEM 方法应用于葛洲坝枢纽工程土石方量计算的实际案例[11]；

2.改进的约束不规则三角构建算法

数字高程模型（DEM）主要通过规则格网模型和不规则三角网（TIN）模型来实现对一定区域内地形地貌的描述。其中，TIN 模型是将区域内不规则分布的数据点通过特定的三角剖分规则构建三角网，形成连续的三角单元,从而描述特定的地形地貌。

由于TIN 模型可以利用有限的离散点实现特定区域的地形地貌描述，因此,可以非常好地与工程中地形采样测量方式结合，并根据地形地貌复杂程度调整采样测量方案，准确描述复杂条件下的地形地貌。

因此，本文在Delaunay 剖分法构造约束TIN 算法的基础上，发展了改进的约束不规则三角构建算法，在无约束的Delaunay 三角网中将工程区域边界作为约束进行插入，并进行局部优化，生成用于土方量计算的约束TIN 模型。该算法主要包括以下几个步骤：

2.1 定位约束边界线起始端点处三角单元

要实现工程区域作为约束边界插入到无约束三角网中，首先需要将边界线端点所在的三角单元定位出来。本文定义了以下算法来实现该功能。

Pn(X,Y) 为边界线端点坐标；n 为端点编号；Dm(xi,yi) 为三角单元三个顶点坐标，其中，m 为三角单元编号；i 为顶点编号（如图 1 所示）：

根据点与三角单元的几何关系，可以定义出点与三角单元边ij 的位置关系判断式，如式（1）所示：

当计算结果ξij=0 时，说明点Pn在三角单元边ij上，若ξij≠0，则根据符号可以判断在边ij 的相应一侧；于是利用点P 与三角单元D 三条边的位置关系，可以判断出P 在三角单元D 的内部或者在某一侧边线外侧。

图1 端点与三角单元坐标定义

图2 三角网遍历过程

边界区域确定后，指定边界的起始点，不断重复上述过程遍历三角网，即可将约束边界起始端点所处的三角单元位置找到（如图2 所示）：

2.2 确定约束边界影响域边线

图3 约束边界影响域边线

在初始定位完成后，从该三角单元处开始寻找下一个边界端点所处三角单元。根据两线段相交的判断准则，即两条线段端点分别同时位于其中另一条两侧时，可知在使用式（1）继续进行三角单元遍历过程中，可以同时筛选出所有被该边界线穿越的三角单元，以及由这些三角单元外边包围形成的影响区域的外包络线，黑色实线（如图3 所示）：

2.3 优化约束边界影响域三角网

在完成上述两个步骤后，已约束边界线作为起始边，在边界影响区域内进行三角网重建，针对约束边界进行三角网的优化，构建将工程区域边界作为约束的TIN 模型。

3.基于改进算法的土方量精确计算原理

本文利用上述改进的约束不规则三角构建算法，将工程区域边界作为约束重建三角网，建立起包含边界约束的TIN 模型。该约束TIN 模型具备准确描述工程区域边界上的复杂地形地貌的优势。

在此基础上，可以进一步确定所有包含在工程区域边界内的三角网，将地面高程完整投射在约束区域上可以得到原始地形TIN 模型，将设计高程投射后即可得到设计地形TIN 模型。利用DEM 方法进行土方量计算的本质就是计算工程区域内的原始及设计地形TIN 模型中每对对应三角单元之间形成的三棱柱体积的计算与累加，如式（2）所示：

在指定场平工程设计高程后，即可根据边界约束TIN 模型计算出每个三角单元上的土方填挖量，进而累加得到总的土方填挖量，实现场平工程区域内土方量的精确计算。

4.改进算法的土方量精确计算案例

本文以浙东地区位于丘陵的某500KV 变电站场平工程为例，应用等高线法、方格网法及本文的改进算法等多种方法分别计算了土方量，并进行了对比。该站区内场平工程实际总挖方量为1891596m3，总填方量为1890751m3。

表1-3 分别给出了利用等高线法、方格网法以及本文改进算法计算的总土方量，表4 给出了三种计算方法得到结果与实际工程总土方量的对比。由此可见，本文的改进算法可以有效减小土方量计算的误差，实现优化场平工程土方量计算的精度。

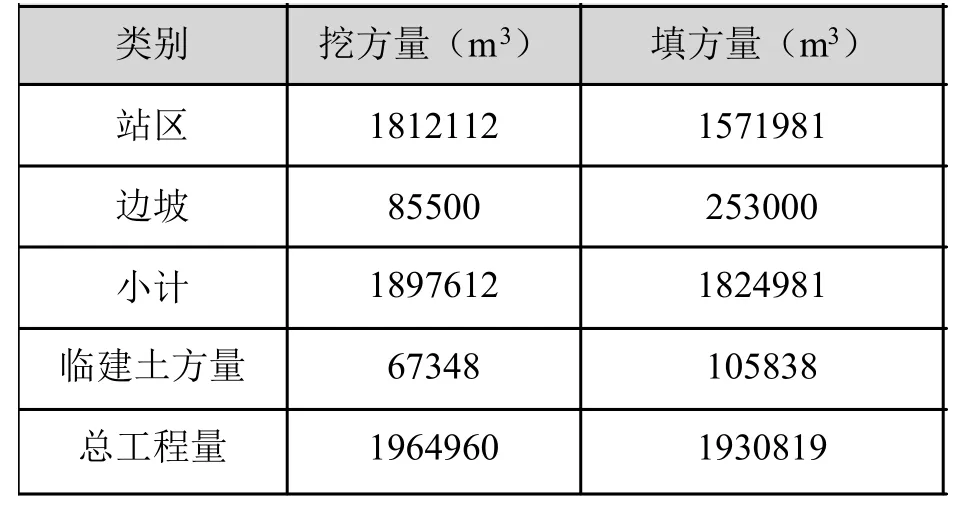
表1 等高线法计算土方工程量

表2 方格网法计算土方工程量

表3 改进算法计算土方工程量

表4 不同方法计算结果对比

5.结束语

为了实现适用于浙东山地区域复杂地形地貌的土方工程量精确计算，本文在Delaunay 剖分法构造约束TIN 算法的基础上，发展出一种改进的约束不规则三角构建算法，在无约束的Delaunay 三角网中将工程区域边界作为约束进行插入，生成用于土方量计算的约束TIN 模型，进而实现土方工程量的精确计算。在此基础上，本文分别给出了利用等高线法、方格网法以及本文改进算法计算的总土方量，并与实际工程总土方量进行了对比，结果表明本文的改进算法可以有效减小土方量计算的误差，优化场平工程土方量计算精度。