灌区广义水资源不确定性多目标优化配置
岳 琼,郭 萍,唐毅宽,赵 敏
(中国农业大学中国农业水问题研究中心,北京 100083)
经济社会发展、人口激增以及气候变化等因素加剧了水资源短缺的危机。2018年我国农业用水量占全国总用水量的61.4%[1],农业作为最大的用水主体,面临着前所未有的用水挑战。如何科学优化且合理配置有限的农业水资源,提高水资源综合利用效益,对保障区域粮食安全以及农业的可持续发展具有十分深远的意义[2]。
近些年,针对农业水资源优化配置问题的研究较多,经济效益最大成为了优化模型的主要目标[3-6]。但是一味追求经济效益,势必会对资源环境产生不可逆转的影响,阻碍区域农业的可持续发展。因此,多目标规划方法受到越来越多的关注。例如,张妍等[7]以社会效益、资源效益及经济效益为目标,构建了多目标农业水资源优化配置模型。王玉伟等[8]考虑了农业生产净效益与地下水位埋深,构建了井渠灌溉水资源优化配置模型。郭萍等[9]以灌区总效益最大和用水效益最大为多目标,对黑河中游农业水土资源进行优化配置。王安迪等[10]基于节水-经济-生态目标,建立了多目标水资源规划模型,以缓解灌区水资源短缺和生态环境恶化问题。这些研究能够为区域农业水资源管理提供丰富的理论指导和方案支持,但也存在一定的局限性,包括:(1)以往研究大多针对灌溉用水总量或作物全生育期需水量进行分配[11-12],引入水分生产函数反映各生育阶段产量-水分关系,并对各生育阶段内灌溉水资源进行优化配置的研究较少[3,13]。实际上,在关键生育阶段的缺水减产,不能通过对其他阶段灌溉更多的水量来弥补。(2)以往研究多数忽略了农业灌溉水资源优化配置系统的不确定性,例如来水量的随机性、管理者的模糊决策以及统计信息的不精确等[14-15]。同时,由系统不确定性因素导致的系统违规风险也不容忽视[16-17]。(3)以往研究中多数是以实体水资源作为研究对象,忽视了作物生长过程中与作物蒸发相关的“隐式水”。事实上,这部分虚拟水资源能够反映更真实的作物需水情况,在研究中考虑虚拟水资源,能够帮助决策者制定更合理的水资源配置方案[18]。
针对以上问题,本研究构建了模糊可信性随机多目标农业水资源优化配置模型,并实例应用于湖北省漳河灌区以验证模型的可行性和实用性。模型包含以下几个要素:(1)引入Stewart等[19]的水分生产函数,体现相同供水量在不同生育阶段的差异性,实现作物各生育阶段内灌溉水资源的高效利用;(2)采用随机期望值多目标模型[7]表征来水的随机性,采用模糊数学规划方法处理系统不确定信息;(3)引入模糊可信性约束规划衡量系统违规风险,该方法不要求所有的约束必须严格满足,相反,只需在给定的违规概率/置信水平下部分满足;(4)引入水足迹的概念,以农业净经济效益最大和绿水利用占比最大为优化目标,设置不同的目标权重组合,以期为漳河灌区农业水资源管理提供安全、高效的决策方案。
1 水资源优化配置模型构建
1.1 目标函数
将灌区内各灌溉分区作物各生育阶段配水量作为决策变量,兼顾社会经济发展目标与灌溉节水目标,建立农业水资源不确定性多目标优化模型。目标函数为:
(1)社会经济目标:净经济效益最大。净经济效益是决策者重点关注的指标,净效益目标反映了灌溉对当地经济发展的影响。灌区总的灌溉净效益等于总灌溉收益减去总成本。优化模型引入Stewart模型来表征作物产量对供水量的响应,与作物价格相乘得到总灌溉收益。总成本包括总种植成本和总灌溉水费。其中,总种植成本由种植面积与单位面积种植成本相乘得到,总灌溉水费由不同水源灌溉水量乘以相应的单方水价得到。目标函数可以表示为:
(1)
(2)
(3)
式中,F1为系统净效益(亿元);i为农业灌溉分区,取3,分别为荆门市、荆州市和当阳市;h为水文年,取3,分别为丰水年、平水年和枯水年;t为生育阶段,取4,分别为分葉期、孕穗期、抽穗期和乳熟期;ph为h水文年发生的概率;Ai为i分区的种植面积(hm2);R为总收益(亿元);C为总成本(亿元);BY为作物价格(元·kg-1);Ym为作物最大产量(kg·hm-2);bt为t阶段水分敏感指数;ETmax,t为t阶段作物最大需水量(mm);ETa,ith为i分区t阶段h水文年作物实际耗水量(mm);D为单位面积种植成本(元·hm-2);CR,CI分别为水库水源及内部水源水价(元·m-3);RWith为i分区t阶段h水文年水库水源分配水量(mm);IWith为i分区t阶段h水文年内部水源分配水量(mm);η1i为i分区水库水源灌溉水利用系数;η2为内部水源灌溉水利用系数。
(2)资源目标:绿水利用占比最大化。2002年,Hoekstra等[20]首次提出水足迹的概念,用来反映一个地区的产品和服务中所包含的全部水资源量。作物水足迹包括:绿水足迹——入渗到土壤中、被植物生长所吸收的水分,蓝水足迹——地表径流与地下水资源,灰水足迹——稀释水污染所需要的水资源[21-22]。高效利用降水资源,减少灌溉水资源消耗是灌区可持续发展的另一目标。因此,模型的另一个优化目标为绿水利用占比最大,即绿水足迹与水足迹的比值最大,其中蓝、绿水足迹的计算方法参考Liu等[22]。
(4)
ETgreen,ith=min(ETa,ith,EPth),∀i,t,h
(5)
ETblue,ith=max(0,ETa,ith-EPth),∀i,t,h
(6)
式中,F2为绿水利用占比;ETgreen,ith为i分区t阶段h水文年作物绿水耗水量(mm);ETblue,ith为i分区t阶段h水文年作物蓝水耗水量(mm);EPth为t阶段h水文年有效降水量(mm)。
1.2 约束条件
(1)稻田水平衡约束。稻田水层深度随着降水和灌溉补给而升高,随着蒸散发、稻田排水以及渗漏损失而下降。稻田水平衡约束可以反映每个时间段的田间水库补给排泄过程,以及水量存储变化,同时引入了最大和最小水层深度约束,以帮助水层深度保持在适合作物生长的安全范围[23]。
Hith=Hi(t-1)h+PRth+RWith+IWith
-ETa,ith-DWith-Sith,∀i,t,h
(7)
Hmint≤Hith≤Hmaxt,∀i,t,h
(8)
式中,Hith为i分区t阶段h水文年稻田水层深度(mm);PRth为t阶段h水文年降水量(mm);DWith为i分区t阶段h水文年稻田排水量(mm);Sith为i分区t阶段h水文年稻田渗漏水量(mm);Hmin,t,Hmax,t分别为t阶段稻田最大、最小水层深度(mm)。
(2)水库可供水量约束。对任一水文年,分配给各分区各生育阶段的水库灌溉水量总和不能超过可供水量。该约束条件采用可信性约束规划,能够有效揭示最优配水方案如何随着可供水量的变化而变化。
(9)

(3)内部水源供水量约束。对任一分区任一时段任一水文年,其内部水源配水量不应超过该分区该时段该水文年型下的内部水源可供水量。
(10)

(4)作物需水量约束。为保证作物正常生长,各生育阶段的实际耗水量应该在最大到最小需水量范围内。
ETmin,t≤ETa,ith≤ETmax,t,∀i,t,h
(11)
式中,ETmin,t为t阶段作物最小需水量(mm)。
(5)非负约束。
DWith≥0,IWith≥0,RWith≥0,∀i,t,h
(12)
1.3 模型求解方法
求解优化模型的核心在于如何将不确定性多目标模型转化为确定性单目标模型。本文分别采用可信性测度方法[24]和加权最小偏差法[25]来求解模糊可信性约束规划及随机多目标规划。
(1)模糊可信性约束规划
假设三角模糊变量表达为b=(b1,b2,b3),则对任意的实数x,x≤b的可信性为:
(13)
根据模糊可信性理论,可以将优化模型中的模糊可信性约束公式(9)和公式(10)转化为如下确定性形式:
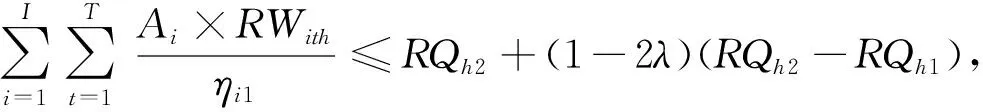
(14)
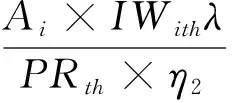
(15)
(2)随机多目标规划。采用加权最小偏差法将所建立的多目标模型转化为单目标模型。
(16)
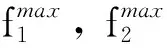
2 实例应用
2.1 研究区域概况
漳河水库灌区位于湖北省江汉平原西北丘陵地区,地跨湖北省工农业生产比较发达的荆门、荆州、当阳三市。灌区南北长约85 km,东西宽约60 km,总面积5 543.93 km2,设计灌溉面积1.74×105hm2,总耕地面积1.632×105hm2,其中水田1.465×105hm2,是湖北省重要的产粮基地之一。灌区属亚热带大陆性季风气候,气候温和,雨量充沛,无霜期长,为农业生产提供了极为有利的条件。漳河灌区的主要耕作方式为水稻与油菜轮作。油菜生育阶段内的降水和地下水可以完全满足其需水量,不再需要补充灌溉。因此,水稻成为了灌区内唯一的农业灌溉用水户。漳河灌区的主要水源有天然降水、漳河水库、中小型水库以及塘堰。其中,漳河水库的配水量在文中称为水库水源,中小型水库及塘堰的配水量统称为内部水源。内部水源能够为农户提供更灵活的供水条件,保证作物及时按需配水。当内部水源不充足时,漳河水库作为补充性水源,以应对作物关键生育期的水资源短缺。尽管漳河灌区降水量充沛,多年平均降水量达884.5 mm,但是其年际和年内变化较大,导致灌区旱涝灾害频发。
在灌区水资源优化配置系统中,可供水量具有随机性和模糊性,统计年鉴中也存在一定的测量误差,这些不确定因素增强了系统的复杂性。对漳河灌区进行不确定性条件下的农业水资源优化配置,能够帮助管理者量化系统的不确定性,权衡系统风险与收益,提出合理的农业水资源规划与管理方案,提高灌区农业生产对环境变化的适应能力,助力灌区社会经济可持续发展。
2.2 基础数据
以漳河灌区3个农业灌溉分区(荆门市、荆州市和当阳市)为研究对象,将中稻分为4个生育阶段(返青分蘖期、孕穗期、抽穗期和乳熟期) ,进行作物各生育阶段用水量优化配置。作物生育阶段划分、水分敏感指数、田间水层深度范围、田间渗漏量以及作物最大产量数据通过参考文献[26]和实地调研获取,如表1所示。参考漳河灌区团林站1988—2018年气象数据,采用FAO-56 P-M公式计算中稻生育期内逐日参考作物需水量,采用作物系数法得到作物各生育阶段实际需水量,各月的作物系数为:5月1.03,6月1.35,7月1.50,8月1.40。最后,累加各生育阶段内的逐日需水量得到该阶段作物总需水量。由于3个农业灌溉分区拥有相似的土壤条件和水文气候条件,因此采用相同的水分生产函数。不同水文年型根据漳河灌区1963—2018年的历史来水数据,采用经验频率分析方法进行划分。频率P<25%对应丰水年,25%≤P<75%对应平水年,P>75%对应枯水年。由于本文的水文参数为55 a长序列,由统计学知识可知,历年经验频率可以近似代替随机事件的概率[17]。不同水文年型下的降水量及水库可供水量参考漳河工程管理局提供的统计数据进行分析得到,见表2。有效降水量由有效系数法计算得到,当次降雨小于50 mm时,有效系数取1.0;次降雨为50~150 mm时,取0.80~0.75;次降雨大于150 mm时,取0.70。水稻市场价格取2.8元·kg-1,种植成本为8 000元·hm-2。各分区种植面积、水分利用效率以及内部水源储水能力见表3。本文采取最小偏差法求解多目标规划模型,不同的目标权重组合会产生不同的优化结果。本文设置了3组权重情景:情景1代表两个目标函数具有相同的权重,即(0.5,0.5);情景2更侧重于社会经济目标,两个目标的权重表示为(0.75,0.25);情景3更侧重于资源目标,两个目标的权重分别为(0.25,0.75)。

表1 作物各生育阶段基础数据
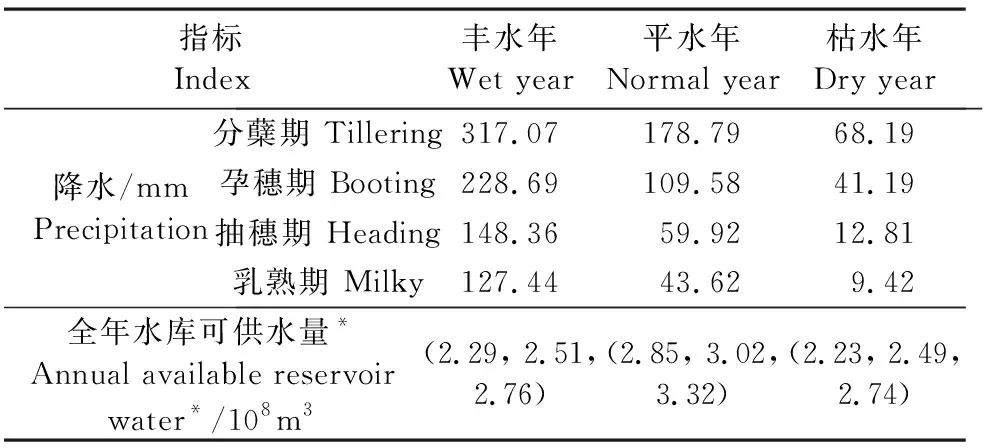
表2 不同水文年型降水及水库可供水量
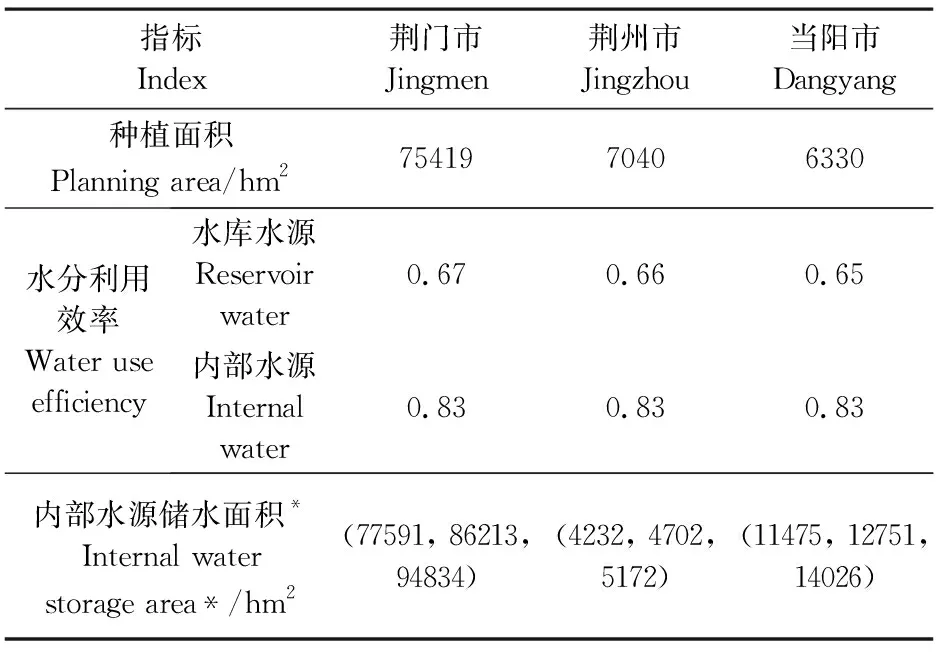
表3 各农业分区基础数据
2.3 结果分析
2.3.1 多目标模型优化 按照前述解法,求解不确定性多目标规划模型,获得不同权重情景及不同可信性水平下的目标函数值(图1)。系统净效益随着可信性水平的升高而降低,相反地,绿水利用占比随着可信性水平的升高而升高,这与模型中可用水量约束(公式(9)和公式(10))直接相关。具体来说,以约束条件(2)(公式(9))为例,由可信性理论可将该不等式转换为:
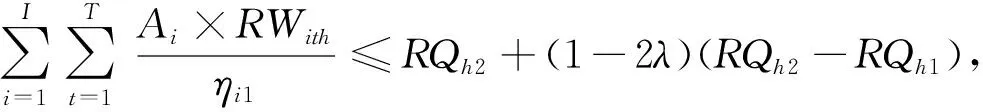
(17)
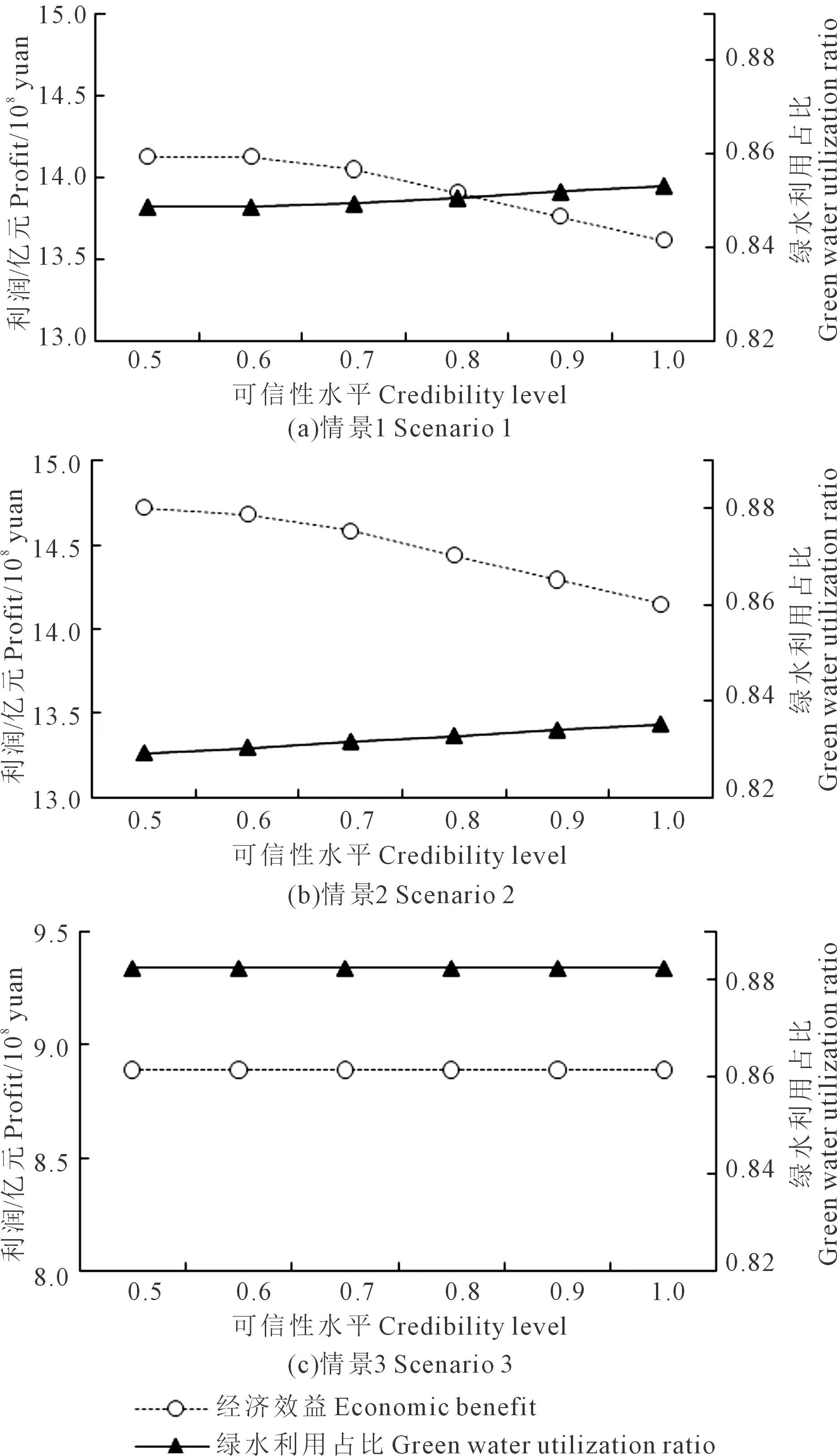
图1 不同权重组合下优化目标值Fig.1 Optimal objectives under different weights scenarios
由此可见,约束右端可供水量随着可信性水平λ的增大而减小,一方面影响了作物的生长发育情况,导致系统净效益降低;另一方面,灌溉水量的减少带来了更高的绿水利用占比。此外,可信性水平升高意味着系统可靠性增强,约束条件的违规风险降低,反之,可信性水平降低则意味着更高的系统违规风险和较低的可靠性。管理者可以根据自身风险偏好选取合适的可信性水平,以达到对系统收益与惩罚风险的不同侧重。如图1所示,当目标函数采用不同的权重组合,多目标模型的优化结果有着显著的差异。系统净效益随着社会经济目标权重的降低而降低,当社会经济目标的权重为0.75时,系统净效益为[14.15, 14.72]亿元;当社会经济目标的权重为0.5时,系统净效益为[13.61, 14.12]亿元;当社会经济目标的权重为0.25时,系统净效益随可信性水平变化基本稳定在8.89亿元。类似地,绿水利用占比随着资源目标权重的升高而升高,当资源目标的权重为0.25时,绿水利用占比稳定在0.882;当资源目标权重为0.5时,绿水利用占比为[0.849, 0.853];当资源目标权重为0.75时,绿水利用占比为[0.829, 0.835]。由结果可以看出,当社会经济目标的权重从0.5降至0.25时,系统净效益显著下降,而绿水利用占比则变化不大,同时目标值在不同的可信性水平下保持稳定,这体现了社会经济目标对权重系数和可信性水平的变化都比资源目标更加敏感。因此,决策者应当谨慎选择多目标的权重系数以及可信性水平,寻求更高效更全面的配水方案。
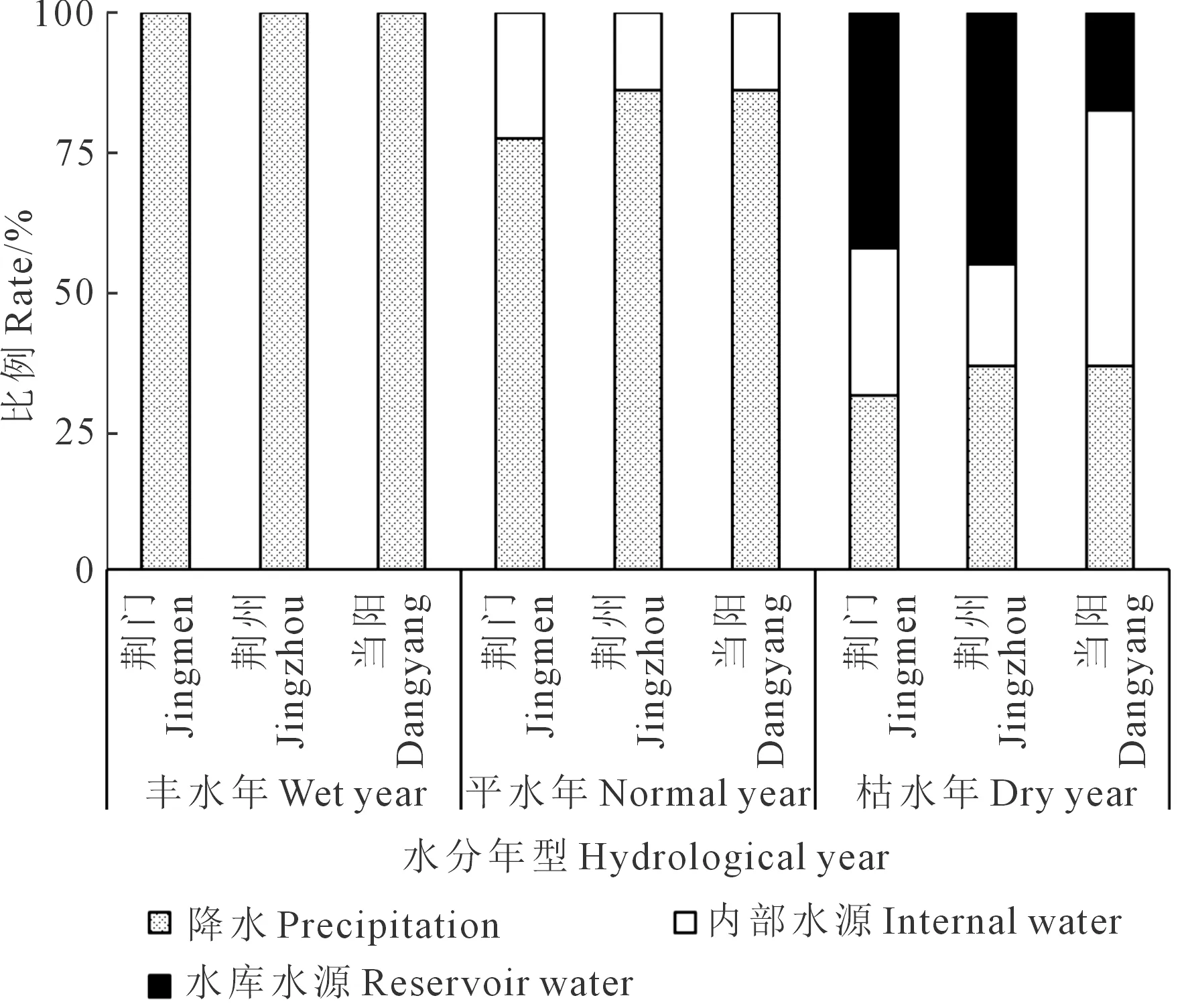
图2 不同水文年型下各分区不同水源配水比例(情景1,λ=1)Fig.2 Ratio of different water sourcesin different subareasunder different hydrological years (scenario 1,λ=1)
图2显示了不同水文年型下各灌溉分区不同水源水量分配比例(λ=1)。值得注意的是,随着来水流量降低,供水水源更加丰富,供水结构从单一的降水供给转变为降水、水库水源以及内部水源共同补给。丰水年时,仅靠降水就能满足作物生长基本需求,灌区内不需要人工灌溉;平水年时,灌区内中小型水库及塘堰的存储水量作为优先水源,被用于作物灌溉;枯水年时,降水只能满足约30%的作物需水量,内部水源和漳河水库在灌溉过程中共同发挥着重要的作用。其中,荆门市、荆州市和当阳市的内部水源分别占各自分区灌溉水总量的39%、29%和72%。由此可见,当阳市的储水能力最强,荆门市次之,而荆州市的储水能力亟需加强。此外,不同水文年型下的水资源分配方案差异显著,体现了本文设置不同来水情景的必要性。图3显示了不同水文年型下各灌溉分区水稻各生育阶段降水、需水和灌溉水分配情况(λ=1)。丰水年时灌区降水量大大超过作物需水量,有效存储剩余的降水资源或充分发掘其利用价值,将大大提升灌区的农业发展水平与资源利用效率。当来水量不充足时,模型倾向于优先满足抽穗期和孕穗期的水量需求,意味着这两个生育阶段对水分的敏感程度更高,因缺水产生的减产现象更严重,这样的结果与各生育阶段作物水分亏缺敏感指数直接相关。由于资源节约目标和来水水平的限制,枯水年作物实际总耗水量几乎达到了作物需水量的下限,建议采取工程节水措施与优化灌溉制度相结合,以实现有限水资源条件下的效益最大化。模型优化结果能够为灌区管理者及农户制定合理的灌溉制度提供理论指导。
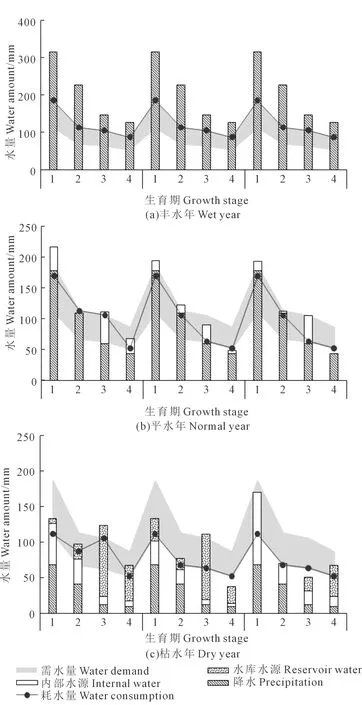
注:1~4:分蘖期、孕穗期、抽穗期及乳熟期。Note: 1~4: tillering stage, booting stage, heading stage, and milky stage.图3 不同水文年型优化配水结果(情景1,λ=1)Fig.3 Optimal water allocation results under differenthydrological years (scenario 1,λ=1)
2.3.2 多目标模型与单目标模型优化方案对比 为验证多目标规划模型的有效性和优越性,分别以社会经济目标和资源目标作为目标函数构建了两个单目标模型,采用与多目标模型相同的约束条件进行编程求解。计算单目标模型与不同权重情境下多目标模型所得优化方案的蓝绿水足迹、绿水利用占比、净经济效益等指标,对比结果见表4。
作物水足迹反映了单位面积产量与耗水量的关系。作物水足迹越高,意味着作物生长过程消耗越多的水资源。从表4可以看出,资源目标的权重越大作物水足迹越高,多目标模型情景3与资源单目标模型的水足迹均为1.824 m3·kg-1,且为最大值,这是由水足迹的概念和目标函数的性质共同决定的。资源目标的目标函数为绿水利用占比最大,因此优化模型倾向于分配更少的水量,导致了更低的作物产量,故而水足迹更大。社会经济目标的权重越大,则灌溉效益越高。当权重为1(即社会经济模型)时,经济效益最高可达14.918亿元。资源模型绿水利用占比达到最大,但是其经济效益最低;社会经济单目标模型优化得到的经济效益最高,但分配方案的绿水利用占比最低;多目标模型能够很好平衡两个目标之间的冲突,其优化结果介于指标最大和最小值之间。例如,多目标模型情景1的经济效益比资源模型增加了4.795亿元,绿水利用占比减小了0.029,充分体现了多目标模型在尽可能节约灌溉水资源的前提下,使得农业生产力达到了较优的水平。因此,与单一目标优化模型相比,多目标规划模型能够兼顾决策者的不同目标,从而提供更全面的方案支持。

表4 不同优化模型下各指标结果对比(λ=1)
3 结 论
1)充分考虑灌区来水的随机性与模型参数的模糊性,兼顾了社会经济发展需求和资源节约目标,构建了以农业净效益最大和绿水利用占比最大为目标的模糊可信性约束随机多目标规划模型,并实例应用于湖北省漳河灌区的农业水资源优化配置研究。
2)模型引入了Stewart水分生产函数,细致地反映了不同生育阶段作物产量对水量的不同响应。模型结果显示,水资源短缺情况下,优先满足抽穗期和孕穗期的作物需水量,能够最小化因缺水造成的水稻减产损失。
3)模型优化结果显示,更高的可信性水平对应更低的系统效益与更高的绿水利用占比,同时意味着更低的违规风险与更好的可靠性。模型优化结果可以帮助决策者权衡系统收益与违规风险。对比单目标规划方案与多目标规划方案,结果表明,多目标规划方案能够平衡不同目标之间的冲突,获得折中的结果,且具有更强的灵活性。
4)总体来讲,漳河灌区降水资源丰富,多目标规划方案的绿水利用占比在0.835以上。然而,在低流量水平下,灌区存在较为严重灌溉水资源短缺现象,在采用优化配水方案的同时,配合一系列工程措施,例如扩大灌区内部水源储水能力、渠系节水工程措施以及稻田节水灌溉模式等,能够更大程度地促进灌区农业可持续发展。

