基于SVR的导航传感器自适应野值检测方法

戴海发，卞鸿巍，马 恒，王荣颖

(海军工程大学电气工程学院, 武汉 430033)

0 引言

综导系统是舰艇收集各导航传感器数据、进行集中处理并分发到各个用户的重要部件。舰载导航传感器的种类和数量较多，再加上海洋和电磁环境复杂多变，因此导航传感器的实际测量数据总是存在一些异常的值，这些异常测量值一般称为野值。如果不对这些野值进行处理，直接输入到综导系统的信息集成模块进行融合，就会影响信息融合的结果，甚至使融合结果完全不可信。因此，在信息融合之前对野值进行检测和处理具有相当重要的必要性。

在实际工程上，处理野值的方法主要有两种思路：一是利用外部传感器的辅助进行野值的检测。主要的方法有基于差值的3σ准则法、基于卡尔曼滤波器的χ2检验法[1-4]、基于小波分析的方法[5-6]等，其中3σ准则法需要基准数据，而χ2检验法依赖准确的系统噪声和测量噪声矩阵，基于小波分析的方法对渐变故障的检测效果不理想。上述方法最大的问题是都依赖稳定无野值的参考系统，如果参考系统也有可能产生野值，那么在检测到野值时，将无法判断具体是哪个系统发生了信息故障。

另一种思路是只利用传感器自身的历史测量值自主地判断野值。工程上比较常用的是差分技术、时间多项式外推法、ARMA模型预测法[7]、Lagrange插值法[8]等。差分技术利用前后时刻的值作差分，通过判断差分值是否合理来判断测量值是否为野值，该方法只对粗大的野值点有效。ARMA模型预测法通过历史数据训练ARMA模型用于预测当前测量值，但是要求测量数据满足平稳性条件。Lagrange插值法利用历史数据通过插值公式预测当前测量值，对于野值离散的野值点效果较好，但是对于野值连续的情况则效果不理想，有可能出现严重的失真现象。文献[9-10]提出了基于模糊系统的遥感数据野值检测方法，但是模糊规则的确定需要一定的技巧，限制了它的使用范围。

因此，本文提出了一种基于支持向量回归(Support Vector Regression, SVR)的导航传感器野值剔除方法。与Lagrange插值法相比，SVR可以自动地学习舰船的运动趋势，连续受野值点的影响较小，而且能够在没有其他传感器辅助的条件下完成野值检测。该方法的思路是利用在线训练好的模型预测当前的导航参数，如果测量值偏离预测值(残差)且超过一定限度，则认为测量值是异常值，并用预测值代替测量值；如果连续检测出异常值超过长T，则认为系统发生故障，除非故障被清除，否则不再使用该设备的信息。此外，传统的阈值一般是靠经验设定，而本文利用了历史残差数据计算出残差的统计量，然后利用3σ准则构建阈值。

本文首先介绍了SVR及算法的基本原理，然后推导了基于SVR的野值剔除方法，并通过实际海试数据验证了本文所提方法的有效性。

1 SVR原理及算法

利用支持向量机作回归分析的原理是通过非线性映射x→Φ(x)，将多维非线性关系样本组x投影到高维特征空间G中变成线性关系，然后在这个高维特征空间中进行线性回归。给定n个数据样本{xi,yi},i=1,2,…,n，其中，xi为实际观测值，yi为期望值。采用式(1)来估计SVR的回归函数f[11]

y=f(x)=(ω,Φ(x))+b,
Φ∶Rn→G,ω∈G

(1)

式中，b为偏置量；ω为高维特征空间G中的矢量；Rn为n维实数空间。

如图1所示，SVR回归的目标是找到一个超平面使得到超平面最远的样本点距离最小，因此得到优化目标函数为

(2)

满足以下条件

(3)

上述优化模型可以看成一个二次规划问题，利用 Lagrange对偶形式，并引入核函数表达式，则式(2)可转化为

(4)

图1 SVR示意图Fig.1 Support vector regression diagram

其约束条件为

(5)

(6)

上述过程需满足KKT(Karush-Kuhn-Tucker)条件[12]，即

(7)

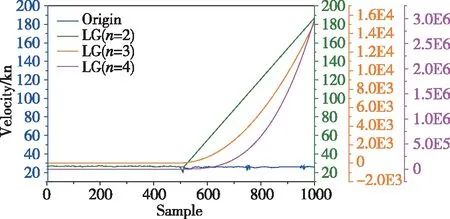
由式(7)可以看出，对任意一个样本(xi,yi)都有(C-αi)ξi=0，且αi(f(xi)-yi-ε-ξi)=0。于是，在得到αi后，若0<αi

(8)

2 基于SVR的野值剔除方法

导航设备的当前导航参数与过去的导航参数具有相关性，理论上可以找到某个函数来表达这种关系，但是这种函数往往是高度非线性的，关于模型的阶次缺少先验知识，而且相关的自变量一般是多维的，传统的回归方法很难解决这类问题。此外，对于样本(x,y),传统回归模型通常直接基于模型输出f(x)与真实输出y之间的差别来计算损失，当且仅当f(x)与y完全相同时，损失才为零；与此不同，SVR假设能容忍f(x)与y之间最多有ε的偏差，即仅当f(x)与y之间的差值绝对值大于ε时才计算损失。正是由于这一特点，使得SVR避免了过拟合的问题[13]。因此，本文采用了SVR的方法来建立这样的函数关系。

对于导航传感器的输出时间序列{x1,x2,…，xt} ，如果根据xt的历史数据预测当前时刻的数据xt+1，则可以建立映射f∶Rm→R，满足[14]

(9)

式中，m为预测函数中使用的历史数据的个数，即模型的阶次。

为了利用第1节的SVR算法来训练预测函数，需要采用窗口大小为N的滑动窗技术，并对k时刻存储的历史窗数据序列{xk-N,xk-N+1,…，xk-1}进行重构，将数据序列转化为矩阵形式，作为SVR的学习样本。构造的学习样本(X,Y)为

(10)

对SVR进行训练的回归函数为

(11)

其中，Xi表示矩阵X的第i行，Yt表示矩阵Y的第t行。本文选取的核函数为高斯径向基核函数，其表达式为

(12)

通过对样本的学习可以得到SVR的模型，从而得到当前时刻的预测值为

(13)

式中，Xk=[xk-m,xk-m+1,…,xk-1]。

计算预测值与实际测量值之间的差值

(14)

野值判定原则为

(15)

(16)

进而确定阈值为

T=3σδx

(17)

通常对于野值的处理都是直接剔除，然而这样会导致信息的缺失，不利于后续的信息融合。因此，本文选择重构的思路，具体的重构方法为当检测出测量值为野值时，利用SVR的预测结果代替测量值。

3 试验与分析

为了验证本文所提出算法的有效性，选取船舶的实测数据做实验，并与Lagrange插值法进行对比。实测数据是在某次航海试验中采集得到的数据，船上搭载的导航设备有惯导、卫导、电磁计程仪和天文导航系统等。海试的航行轨迹如图2所示。高斯径向基核函数的宽度参数取为σ=4；损失函数ε=0.01；滑动窗宽N=20；模型阶数m=5。本文所使用的算法是在开源代码库LibSVM的基础上进行修改实现的，使用的仿真平台为MATLAB。

图2 海试航行轨迹Fig.2 Sea trial sailing track

以电磁计程仪的速度信息为例(图3)，原始测量数据中含有较多的野值点。取其中长度均为1000个样本的2段数据进行分析，其中一段只含有少量离散的野值点，另一段含有几处连续的野值点，分别利用Lagrange插值和SVR的方法对数据进行野值处理。

图3 电磁计程仪原始数据Fig.3 Electromagnetic log raw data

1)场景1

在场景1中，样本中的速度测量值含有少量离散的点，且速度保持在基本平稳的状态下，Lagrange插值法的插值点数设为n=2，得到的结果如图4所示。

图4 场景1不同野值处理方法结果对比Fig.4 Comparison of different outliers processing methods in scenario 1

从图4中可以看出，在该场景中Lagrange插值法和SVR算法都能够有效地去除离散的野值点，而且SVR算法对波动值的估计值更加平滑。从表1可以看出，SVR算法的计算时间比Lagrange插值法只多了11ms,但是检测成功率提高了8%。这表明SVR算法建立的预测模型比较准确，在一定程度上能够抑制噪声的影响。

表1 不同检测方法的性能对比

2)场景2

如图5所示，场景2中，舰船运动状态不稳定，存在加速和减速运动，速度的测量值存在3处连续的野值群(如图6中蓝色虚线椭圆所标示)。此时，不能够确定Lagrange插值法的插值点数，因此分别设定了几种插值点方案，得到的结果与真实测量值的对比如图5所示。图6展示了使用本文所提出的方法估计的结果与真实测量值的对比情况。

图5 场景2 Lagrange插值结果Fig.5 Lagrange interpolation results in scenario 2

图6 场景2 SVR结果Fig.6 SVR results in scenario 2

从图5可以看出，利用Lagrange插值法得到的结果刚开始与实际测量值比较接近，说明该方法能够剔除少数离散的野值点；但是从第500个数据点开始，估计值逐渐偏离真实值，而且随着插值点数量n的增加，偏离得越激烈。这是因为此时出现了较多连续的野值点，而Lagrange插值法会将误差逐渐累积，插值点个数越高，模型的阶次越高，误差膨胀得越快。在1000s时，速度误差分别达到160m/s、1.6×104m/s、3×106m/s，已经完全失去了修正功能，这说明任意插值点数的Lagrange插值法无法检测出连续的野值点。

从图6可以看出，蓝色椭圆虚线标示出的3处连续的野值已经被基于SVR的方法有效剔除，得到的结果与真实测量值比较吻合，而且平滑性较好，较好地反映了舰船的真实运动速度。这表明基于SVR的方法对于导航传感器连续野值点的情况具有较好的抑制作用。表2展示了不同野值检测方法在场景2下的计算时间和检测成功率，从表2中可以看出，SVR算法在该场景下依然具有较少的计算时间和较高的检测成功率。

表2 不同检测方法的性能对比

4 结论

针对Lagrange插值法无法处理连续野值的问题，本文提出了一种基于改进SVR的导航传感器自适应野值检测方法。该方法结合了SVR只需要小样本数据就能够准确建模和3σ准则计算简易的优点，利用SVR在线建立舰船的运动模型对测量值进行实时预测，并利用3σ准则自适应地计算阈值；然后通过比较阈值与预测残差来判别测量值是否为野值点，如果测量值被检测为野值点，则用SVR的预测值替代该野值点。海试实测数据表明，本文提出的方法能够在存在连续野值点的情况下检测出野值点，同时得到较好的传感器真实测量值的估计，而且算法简单容易实现，具有较好的工程应用价值。