气体轴承斯特林制冷机双级被动减振系统研究

周吉 韩彦伟 张子建 王波 张银 刘志敏

（1 北京空间机电研究所 中国空间技术研究院空间光学遥感器技术核心专业实验室，北京 100094）

（2 河南科技大学 土木工程学院，洛阳 471023）

（3 南京航空航天大学 航天学院，南京 210016）

（4 中国电子科技集团第十六研究所，合肥 230088）

0 引言

近年来我国对机械式制冷机的需求越来越迫切，而振动是影响制冷机空间红外探测、超导滤波等应用的一个关键因素[1-4]。相比分置式斯特林制冷机，气体轴承斯特林制冷机因其具有效率高、体积小、质量小、寿命长等优点，在近年得到了广泛关注。2002年，美国将全球首台气体轴承制冷机应用于航天，至今投入航天应用的此类制冷机已有近百台[5-6]。我国气体轴承制冷机的空间应用与美国有很大差距。

与分置式斯特林制冷机类似，气体轴承制冷机由于采用一体化设计，本身振动输出较大，要在空间获得应用与推广，必须更好的解决微振动抑制问题，由于其结构和工作原理与分置式制冷机存在一定差异，微振动抑制手段亦有所不同。国内外诸多机构已针对机械制冷机的振动形成机理及主、被动减振技术开展了研究工作。国内方面，文献[7]介绍了低温制冷机的振动测量方法和振动形成机理的研究进展，并对当时低温制冷机的主要减振措施进行了整理与归纳；文献[8]研究了线性压缩机冲程幅度对微振动的影响；文献[9-13]对斯特林制冷机振动的产生机理及特征进行了讨论，对制冷机主动减振控制等相关技术进行了研究；文献[14-15]针对斯特林型脉管制冷机的压缩机微振动成因及抑制措施开展了讨论；文献[16]论述了气体轴承斯特林制冷机的振动来源和振动特性，利用梁模型计算了冷指的自然频率，给出了动力吸振器的设计方法，并通过实验验证了动力吸振器可以有效的抑制制冷机的振动输出。

国外方面，文献[17]对2003年前国际上典型的线性驱动空间低温冷却器所使用的各种主动和被动振动抑制系统的典型性能进行了介绍；文献[18]对脉冲管制冷机的主动减振闭环控制系统及算法进行了研究；文献[19]、[20]分别介绍了洛•马公司设计的斯特林制冷机和NGAS空间脉冲管制冷机的主动减振技术；文献[21-26]指出斯特林制冷机中的移动组件的不平衡往复运动产生的振动输出可能会影响图像像质；针对牛津型压缩机、典型的双活塞压缩机及单活塞膨胀机引起的振动输出问题，Veprik等人设计了一种多模态调谐动态吸收器，通过吸收器产生的动态响应（力和力矩）用来有效削减制冷机的振动输出，此外，他们还指出在一些特殊的应用场合，若采用纯被动的振动控制方法，就整体系统效率而言，其潜力可能优于主动减振系统[26-27]。

综上可以看出，针对气体轴承制冷机减振的研究多集中在主动减振策略及动力减振器的研制，而针对采用被动减振隔振技术来进行系统减振的研究较少。考虑到气体轴承制冷机采用主动减振方案对控制器时效性和精度要求较高，且控制器自身需要电能输入造成能源利用率下降，本文提出一种双级被动减振的设计方案，通过建立三自由度非线性动力学模型，分析了不同阻尼、不同刚度、不同重力、不同外部激励力时制冷机本身的振动响应变化，通过试验与仿真，验证了模型和仿真方法的有效性。

1 物理模型

气体轴承制冷机在布置安装时通常有固支法和悬吊法两种方式。其中固支法由于单独使用时，制冷机对外振动输出较大，通常与主动减振控制系统结合使用，由于涉及电子学和精密控制算法等理论，实现起来较为复杂，且自身需要消耗一部分能源，间接降低了制冷机的制冷效率。针对单侧式气体轴承制冷机这一特定结构（图1展示了气体轴承制冷机的实物及其内部组成），本文基于悬吊法提出一套无需外部能量输入的斜弹簧支撑+被动减振器协同作用的双级被动减振系统，气体轴承制冷机由 8个阻尼和刚度适宜的弹簧悬挂吊装在固定支架上，以消除制冷机轴向振动对制冷系统的影响。之所以选用8根阻尼弹簧是基于弹簧数量应是偶数、几何对称性以及弹簧数量不宜多（如 12个）等三方面的考虑，否则会造成工程实现比较困难。双级被动减振结构如图2所示，由于气体轴承斯特林制冷机壳体上无预留弹簧安装孔，因而采用附加吊装工装的方式进行悬挂弹簧的安装。基于简化和壳体电机散热需求的考虑，吊装工装为尺寸和制冷机壳体尺寸匹配的半圆形卡箍，上面预留弹簧安装孔和紧固螺钉孔；制冷机通过吊装工装连接到固定工装支架上；制冷机尾部安装有动力减振器，通过8根斜弹簧和动力减振器共同构成双级耦合减振系统。

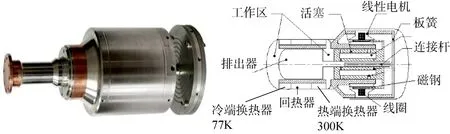
图1 气体轴承斯特林制冷机实物图及内部结构Fig.1 A gas bearing Stirling cryocooler product with its internal structure display

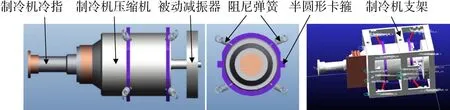
图2 双级耦合减振布置和动力学模型示意Fig.2 A schematic diagram of two-stage coupling damping arrangement

2 三自由度系统非线性动力学建模及振动响应分析

2.1 动力学模型的建立

基于实物建立三维力学模型，定义活塞运动方向为Y向，重力反方向为+Z方向，垂直于YZ平面，按右手定则确定X方向。考虑制冷机X、Y、Z三个方向的自由度，在8个弹簧阻尼和刚度系数均相同的前提下，基于对称性建立制冷机三自由度系统的非线性动力学模型，如图3所示。

在本文仿真和试验验证过程中，各系统参数取值情况如表1所示。

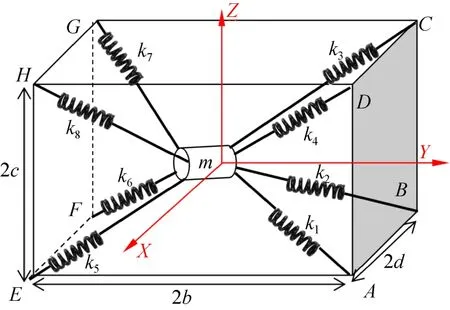
图3 三自由度制冷机系统的非线性动力学模型Fig.3 The nonlinear dynamic model of a three-degree-of-freedom chiller system

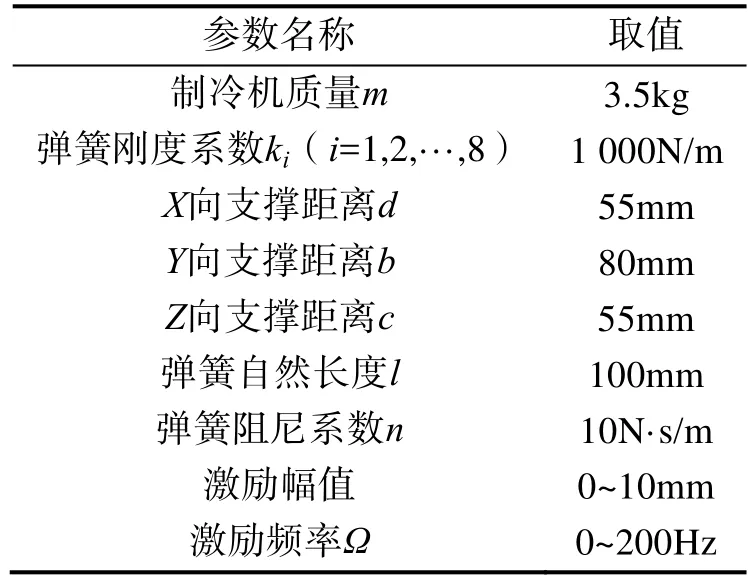
表1 系统参数的取值Tab.1 The value of the system parameters before optimization

为了推导出三自由度系统的动力学方程，需要运用到Lagrange方程，其中涉及到动能、势能、阻尼函数、广义外力几个量。首先，三自由度制冷机系统的动能Ek为

制冷机系统中弹簧的弹性势能EP为

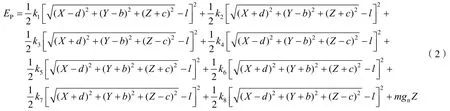
式中gn为标准重力加速度。

8个弹簧所构成的系统的阻尼用瑞利阻尼函数ψ来表式，形式为

广义外力定义为

式中F为外部激励力幅值；Q1、Q2分别为用正余弦表示的广义外力。根据表1中制冷机系统的参数值，计算得到不同平面的非线性势能函数，如图4所示。

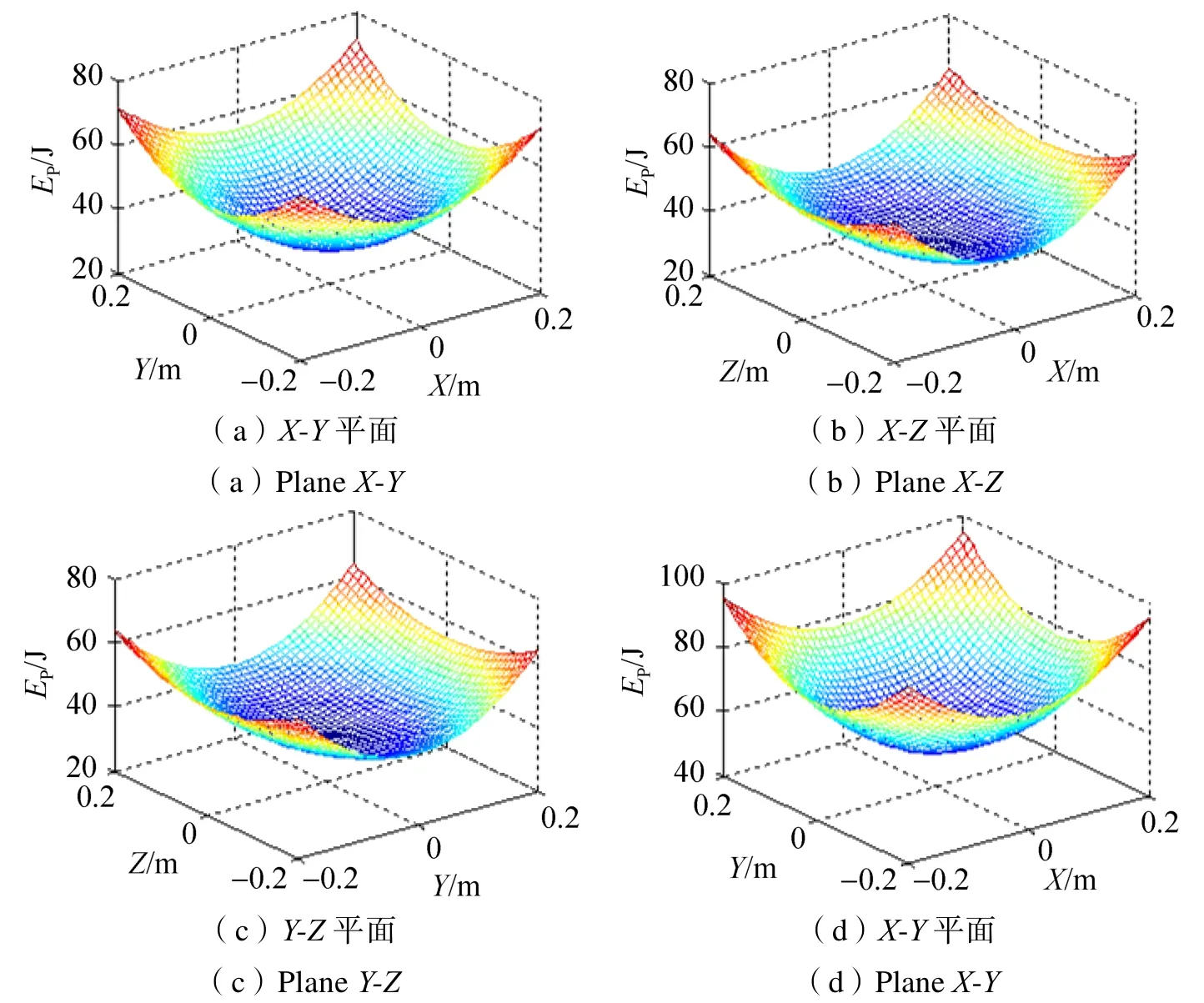
图4 制冷机不同平面的非线性势能函数Fig.4 The nonlinear potential energy function

将式（1）~（4）代入Lagrange方程，得到三自由度系统的动力学方程为

方程（5）是一个复杂非线性动力学方程，该方程无法用解析法直接研究。

2.2 运动方程

针对上文推导出的运动方程，利用量纲一形式变换

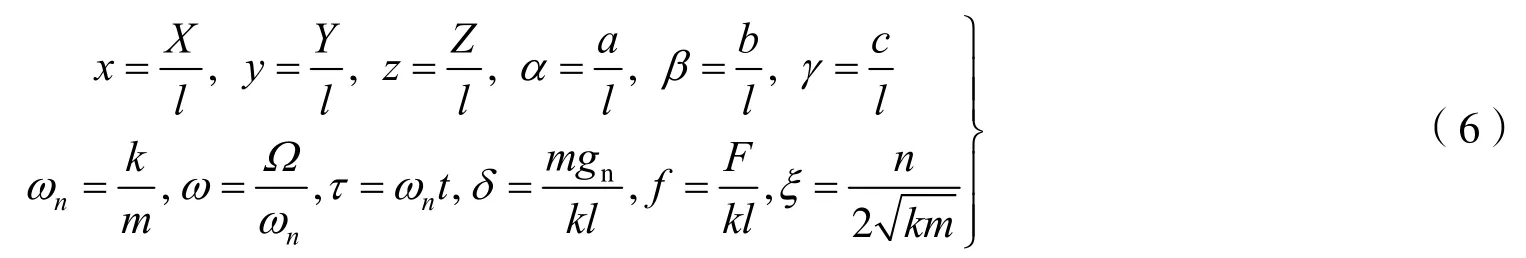
式中量纲一处理的参数有位移（x，y，z），距离参数（α，β，γ），系统固有频率ωn，频率比ω，时间τ，重力系数δ，力f，阻尼系数ξ。将式（6）中各参数代入式（5），可得到变换后的运动方程为

式（7）运动方程也是一个高维非线性动力学方程，具有复杂的振动响应，获得其解析解非常困难。

2.3 数值仿真

采用数值积分Runge-Kutta法，对方程（7）所示的非线性制冷机振动系统进行数值模拟。仿真系统参数根据试验设定为m=3.5kg，d=0.055m，b=0.08m，c=0.055m，l=0.10m，k=1000N/m，n=10N·s/m，F=10N，参照式（6）进行处理，得到α=0.5，β=0.7，γ=0.5，δ=0.3，f=0.1，ξ=0.25。图5为仿真计算得到的幅频响应，将其与后续试验测得结果进行比较，图中“◇”表示试验测得的X方向幅值，“×”表示试验测得的Y方向幅值，“＋”表示试验测得的Z方向幅值。

从图5中容易看出激振频率出现在频率120Hz附近，其加速度峰峰值与试验测得的峰峰值加速度基本接近，基本验证了仿真方法的正确性。造成微小差异的原因主要是对制冷机几何结构有所简化，将其当作质点来研究所致。

在上述基础上，本文又相继研究了减振器阻尼、弹簧刚度、重力加速度和电磁力激励对特定频率下加速度幅频响应的影响，图6分别展示了不同条件下加速度幅频响应随频率的变化规律。

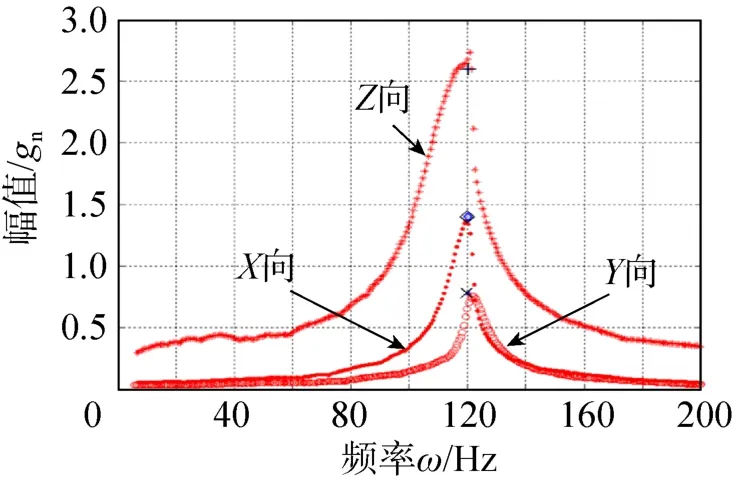
图5 幅频响应曲线Fig.5 Amplitude-frequency response curves

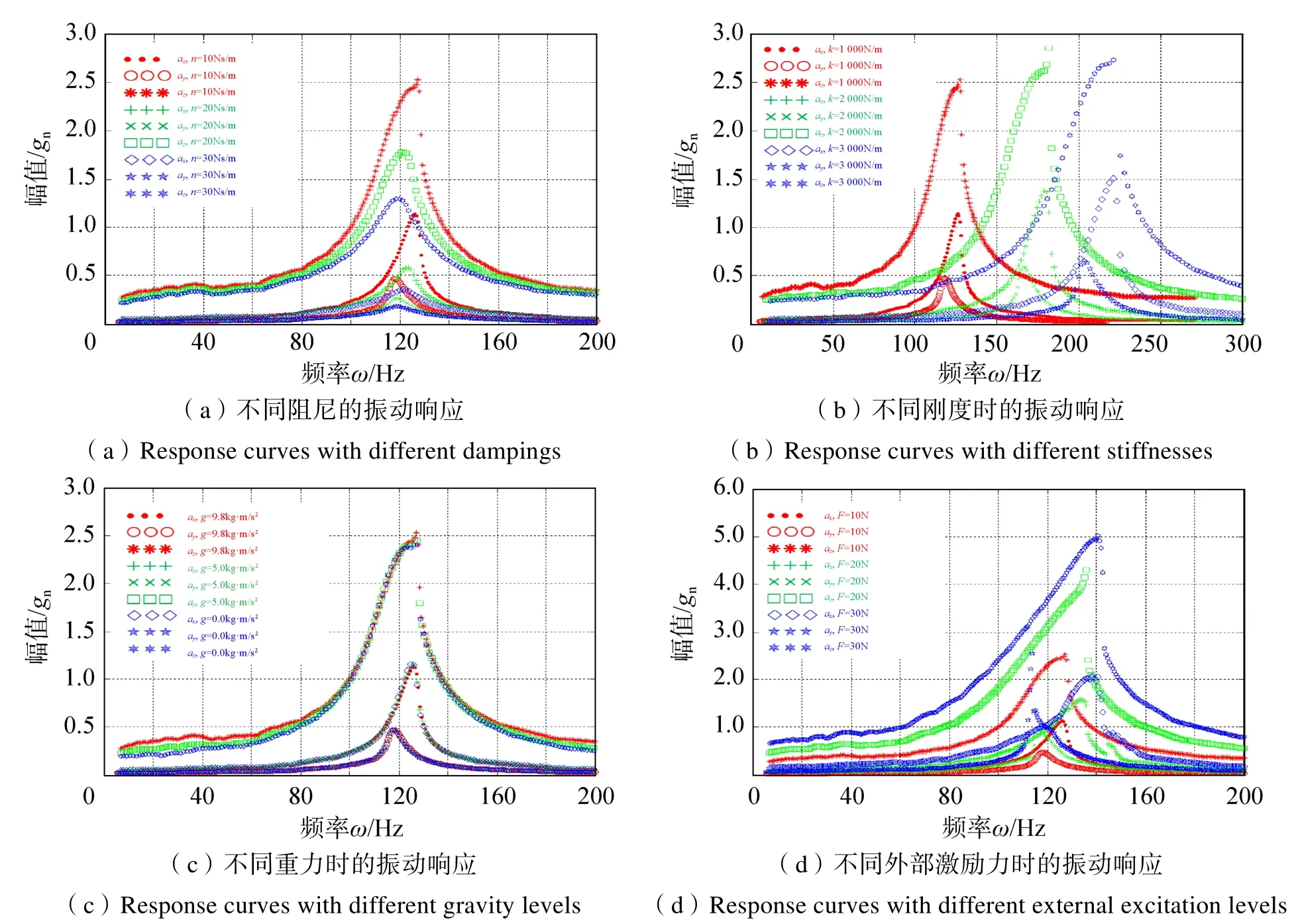
图6 不同情况下加速度幅值随频率的变化Fig.6 Amplitude-frequency curves

图6（a）显示了不同减振器阻尼条件下加速度幅值随频率的变化。可以看出：当阻尼取值增大时，在x，y，z三个方向的振动幅度都会减小，在峰值处减小的幅度满足az＞ax＞ay，随着减振器阻尼的逐渐增大，加速度幅值的减少逐渐减慢；另外还可以发现，减振器阻尼的变化并不会对加速度幅值所对应的频率峰值位置产生影响。

图6（b）显示了不同弹簧刚度时加速度幅值随频率的变化。总体来说，在相同刚度条件下，加速度变化幅度始终满足az＞ax＞ay，当刚度增大时，在x，y，z三个方向振动幅度都会增大，且刚度越高，振幅增加的幅度越大。最大振幅位置对应的频率点往高频移动，而在激励频率60Hz处的响应幅值会较其他频率处有所减小。

图6（c）显示了不同重力加速度时加速度幅值随频率的变化。可以发现：当考虑重力减小时，在x，y两个方向共振响应幅值几乎不变，而在z轴方向振动幅值略有减小。由此可以推断重力主要对其力施加方向起作用，对其他方向影响很小，且失重状态有利于减少振动响应幅值。

图6（d）显示了不同制冷机电磁激励条件下加速度幅值随频率的变化。可以发现：当增大电磁力时，x，y，z轴三个方向共振响应幅值都会增大；此外，当电磁力增大时，ax、az和ay三个方向的加速度响应曲线峰值都有向高频方向移动的趋势，且偏移幅度az＞ax＞ay。

3 试验研究

3.1 试验测试

根据表1中设定的系统参数搭建一套双级被动减振系统，测试工况为：激励功率为100W时，无杜瓦水平放置状态的制冷机的振动测试。微振动测试采用固支法，制冷机通过双级被动减振结构连接至测试支架上，将制冷机测试支架固定在试验台上，5个测点位置对应安装5个加速传感器，位置分别为制冷机尾部动力减振器（测点1），冷指热端（测点2），冷指冷端（测点3），支撑工装中部（测点4）和支撑工装与振动台连接处（测点5）。其中测点4、5主要是为了评价通过双级被动减振装置与整星连接时，从制冷机本体传至卫星本体的微振动量级。

制冷机微振动测试采用北京航空航天大学研制的微振动测力平台开展，本文测试中用到的加速度传感器为PCB三向加速度传感器，测量灵敏度为1 000mV/gn，频率范围1~5 000Hz；数据采集设备采用由比利时LMS国际公司生产的LMS CADA－X模态试验分析系统，具有4路控制通道，48路采样控制通道，采样精度24位。

3.2 测试结果

测试过程中，5个三向加速度传感器的坐标与制冷机组件的坐标一致。本文仿真中只针对制冷机本体上的加速度影响进行讨论，而测点2位于制冷机本体中部，其结果基本能反映出制冷机的振动响应情况，故本文仿真中仿真结果主要与测点 2处的测试结果对比。

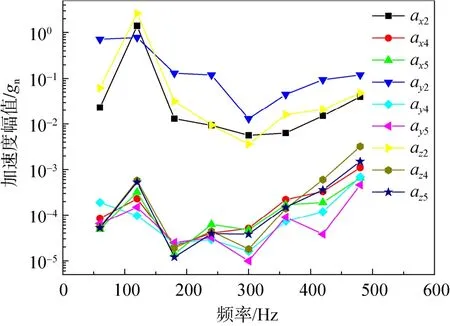
图7 不同测点处不同方向加速度幅值随频率的变化Fig.7 Change curves of acceleration amplitude with frequency in different directions at different measuring points

图 7为通过试验获得的不同测点处不同方向加速度幅值随频率的变化（ax2表示测点2处x方向加速度，其它类似）。可以看出，在激励功率为 100W时，测点2处加速度峰峰值出现在两倍频120Hz处，其峰值出现位置及加速度量级与仿真结果基本一致，由此表明仿真结果基本可靠。由测点 4、5处的加速度测试结果可以看出，与制冷机本体上的加速度相比，通过双级被动减振机构后，制冷机微振动对支撑基板的影响幅度明显减少。由此可以相信，双级被动减振结构可以有效的减少气体轴承制冷机微振动对外界的影响，是一种有效的隔振减振方式。

4 结束语

针对航天工程中的气体轴承斯特林制冷机的动力学模型，提出了斜弹簧支撑加双级被动减振的方案，实测了单侧式气体轴承制冷机的微振动，并基于实物建立了三自由度非线性振动运动方程，在此基础上研究考虑了不同影响因素作用下，振动响应幅值的变化规律。研究结果表明：三自由度非线性系统能够准确的描述制冷机动力学响应，计算与试验结果具有良好的一致性。振幅响应随着减振器阻尼增大或斜弹簧刚度增大而减小；重力对振幅响应的影响主要体现在施加方向，对其他方向影响不大；制冷机电磁激励增大时，振动幅值也相应增大，且峰值有向高频方向移动的趋势。本文的研究结果可为气体轴承制冷机减振系统的设计与优化提供一些有价值的参考。