基于自适应粒子群优化的粒子滤波跟踪算法

林晓杰 索继东

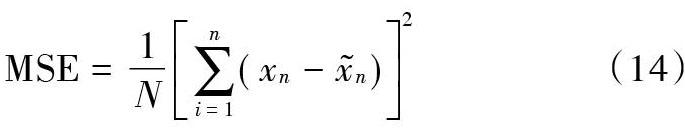
摘 要： 传统粒子滤波算法中在重要性采样部分存在采样粒子位置不精确的问题，可用粒子群优化算法优化，但目前的标准粒子群优化粒子滤波算法会出现粒子局部寻优的情况。对此对算法中的惯性权重和学习因子同时采取自适应调整的方法，平衡粒子的搜索能力以减少这种情况的出现，并且为了解决算法优化后因粒子聚集而造成的多样性缺失问题，对粒子进行随机变异以提高粒子多样性。仿真结果表明，经过改进后的优化算法可有效提高粒子滤波算法的准确性，使跟踪误差减小。

关键词： 粒子滤波跟踪; 粒子群优化; 自适应调整; 搜索能力平衡; 随机变异; 优化算法

中图分类号： TN911.1?34; TP391.9                 文献标识码： A                   文章编号： 1004?373X（2020）17?0011?05

Abstract： The problem of inaccurate sampling particle position exists in the important sampling part of the traditional particle filter algorithm， which can be optimized by particle swarm optimization algorithm. However， the current standard particle swarm optimization particle filtering algorithm may lead to particle local optimization. In this paper， self?adaptive adjustment method is adopted to adjust the inertia weight and learning factor in the algorithm， so as to balance the searching ability of particles to reduce the occurrence of this situation. In order to solve the problem of diversity lack caused by particle aggregation after optimization of the algorithm， the particles are randomly mutated to improve the diversity of particles. The simulation results show that the improved optimization algorithm can effectively improve the accuracy of particle filtering algorithm and reduce the tracking error.

Keywords： particle filtering tracking; particle swarm optimization; adaptive adjustment; search capability balance; random variation; optimization algorithm

0  引  言

粒子滤波基于蒙特卡罗模拟方法实现递推贝叶斯滤波估计[1]，对于系统的过程噪声和量测噪声没有任何的限制，更适合于实际工程中的应用[2]。但是其仍然存在问题，包括采样粒子不准确、多样性缺失等问题[3]。

针对粒子滤波所采样的粒子不准确，造成整个粒子滤波算法正确性大幅度降低的情况，智能算法可以在一定程度上解决这个问题。已经有学者将人工鱼群算法[4]、粒子群优化算法[5]、人工鸟群算法[6]等与粒子滤波算法相结合，对采样粒子进行位置上的调整，用于提高重要性采样阶段采样粒子的准确性。除此之外，还有学者用遗传算法[7]对重采样进行改进，防止粒子退化，增加粒子多样性。其中粒子群优化算法是通过计算粒子的适应度值来对粒子位置和速度进行调整，使粒子能够移动到高适应度位置的地方以提高算法的准确率[8]，但是这种算法存在着局部寻优的情况，容易发生跟踪丢失的情况。

针对智能算法中粒子群算法优化粒子滤波后会出现的局部寻优情况，有学者提出使用自適应惯性权重的方法解决此类问题[9]。除了惯性权重外，学习因子也通常设定为常数[10]，不利于平衡随时间变化的搜索能力，因此，在标准粒子群算法中，有学者对学习因子进行自适应变化来代替常量提高精度[11]。基于这些方法，本文将粒子群算法中对学习因子进行自适应这一措施加以调整后加入到优化算法中，然后对自适应权重的方法也进行调整，通过同时对惯性权重和学习因子进行自适应调整来提高跟踪精度。

除此之外，粒子群在调整位置后会出现过于集中造成多样性缺失的情况，针对这种情况，本文在算法中加入粒子位置变异算法，用以改善粒子过于集中造成的多样性缺失问题。

1  基于粒子群优化的粒子滤波

粒子滤波算法主要用于解决非线性非高斯情况下的目标跟踪，其利用一组随机采样样本对后验概率密度进行假设，用样本均值代替复杂的积分运算[12]。粒子滤波算法可能因为采样粒子的不准确造成算法性能的低下，因此，采用粒子群优化算法对采样粒子的位置进行调整以提高目标跟踪的准确性。基本粒子群优化粒子滤波算法的主要步骤如下：

1） 初始化粒子群。随机抽取[N]个粒子。从先验概率密度函数中随机抽取粒子组成采样粒子集合[{Xn，n=1，2，…，N}]，并且随机赋予这些粒子初始速度为[V1，V2，…，Vn]。

2） 对抽取的粒子利用粒子群优化算法来优化粒子位置。

评价粒子群，计算粒子的适应度值[P（y）]，计算公式为：

式中：[R]为量测噪声方差;[zn]为粒子的量测值;[znn-1]为量测预测值。

设第[i]个粒子的位置为[{xid，d=1，2，…，D}]，速度为[{vid，d=1，2，…，D}]。令[Pid]为粒子[i]个体最优位置;[Pgd]为群体中所有粒子全局最优位置[13]。将粒子的当前适应度值与此粒子的个体最优解[Pid]的适应度值进行比较，若更优，则令此粒子位置为个体当前最优位置。对于每个粒子每次计算得到的适应度值，都与全局最优解[Pgd]进行比较，如果大于[Pgd]的适应度值，则将所对应的粒子位置調整为全局最优位置。按式（2），式（3）更新每个粒子的速度和位置以产生新的种群。

在式（2），式（3）中：[1≤i≤n]，[1≤d≤D];[vid（t）]表示第[t]次循环粒子的飞行速度;[xid（t）]表示第[t]次循环粒子[i]所在的位置;[Pid]表示经过[t]次循环后第[i]个粒子的个体最优位置;[Pgd]表示经过[t]次循环后粒子的群体最优位置;[w（t）]为惯性权重;[c1]和[c2]为学习因子。不断循环此步骤直到满足迭代次数，此时更新后的位置为粒子的最终位置。

3） 权值计算

通过得到的最新量测信息对粒子的权值进行计算，由贝叶斯准则可以得到权值的更新公式：

权值计算更新后，需要对权值进行归一化计算，公式为：

4） 重采样

通过计算算法中的有效粒子数[Neff]的个数，将其与所设定的有效粒子数阈值[Nth]进行比较，判断是否需要进行重采样。

若[Neff

5） 状态输出

2  自适应优化策略

在粒子群优化算法中，可以对粒子的参数进行自适应优化，惯性权重和学习因子的自适应就是其中的一种方法[14]。对两者进行自适应调整可以减少由于局部寻优造成的准确性降低的问题。文献[9]提出了自适应权重调整的粒子群优化粒子滤波算法，降低发生局部寻优情况的概率。本文在此基础上对粒子群优化粒子滤波算法进行惯性权重和学习因子两方面的自适应，并且使用变异算法以提高多样性。

2.1  惯性权重自适应

在粒子群优化算法中，通常惯性权重为一个常数。惯性权重较大，表示粒子有较好的全局搜索能力，较小则更有利于局部搜索。若惯性权重保持不变，粒子的搜索能力不变，会造成局部寻优情况[14]。针对这种情况，可以对惯性权重根据适应度值进行自适应调节。当某一点的适应度值小于适应度均值时，可以将此点认为是远离真实值的点或者陷入局部寻优情况的点，对其惯性权重进行自适应调节，使其能够向更优方向移动，具体优化方法如下：

令[w（t）]为自适应惯性权重，惯性权重的计算方式按式（8）方法进行改进：

式中：[fmin]为粒子适应度最小值;[favg]为当前所有粒子的适应度均值;[F]为当前适应度值;[wmax]和[wmin]分别为设定的惯性权重最大值和最小值;iter表示粒子的最大迭代次数;[t]表示当前的迭代次数。若[Ffavg]，认为粒子位置较好，文献[9]中设定惯性权重为一个常数来表示。本文如式（8）所示，用改进的线性变化来调整惯性权重[14]，让惯性权重随迭代次数减小，使其前期有较好的全局搜索能力，后期有较好的局部搜索能力。

计算得到惯性权重后，通过其对相应的粒子进行位置和速度的调整。每个粒子的速度和位置按照式（2）和式（3）进行迭代，从而提高粒子位置的准确性。

2.2  学习因子自适应

在标准粒子群算法中，学习因子[c1]和[c2]通常被设定为一个常数。其中，学习因子[c1]表示自我认知，即对自身的调整;学习因子[c2]表示群体认知，即对整个种群的信息交流。[c1]的大小决定了粒子局部范围搜索的能力，[c2]的大小决定粒子收敛到最优值的速度[14]，通过对[c1]和[c2]的调节能够控制粒子向最优位置移动的能力。

在算法初期，提高粒子向全局最优位置移动的概率，避免陷入局部最优位置。而到了粒子后期，则希望能够加强粒子移向最优位置的速度，获得高质量的粒子。

[c1]和[c2]设定为一常数。在优化算法中，令学习因子[c1]随着迭代次数的增加而不断增加，相反，学习因子[c2]则随着迭代次数减小。其变化公式为：

式中：iter表示粒子的最大迭代次数;[t]表示当前的迭代次数。通过这个自适应算法，能够动态调整两个学习因子的数值，提高了粒子向最优位置移动的能力。两者的相互配合可以使粒子快速收敛到全局最优位置，从而提高算法的收敛精度。

2.3  变异操作

为了提高粒子的多样性，引入了变异操作。设定一个随机函数rand，再设定一个阈值，对此随机函数进行判断，当此随机函数超过某一个阈值时，对粒子进行变异操作，即随机调整该粒子的位置，避免粒子过于集中，提高粒子的多样性，位置变动公式如下：

式中[Rmax]为粒子的最大追踪范围。

3  改进的自适应粒子群优化粒子滤波算法

根据上面的内容，基于自适应粒子群优化的粒子滤波算法的步骤可总结如下：

1） 初始化。初始化各个参数，包括测量噪声协方差、过程状态协方差、模拟步长、粒子数、进化代数、惯性权重最大最小值等。

2） 重要性采样，从重要性概率密度函数中采样新的粒子[xkiNi=1]。

3） 进行粒子群优化。将所采样粒子作为初代粒子对其进行粒子群优化。在第一代中，粒子的速度由随机函数获取，位置为粒子滤波算法中所提取的粒子的位置，得到此时粒子的速度以及位置。

利用式（1）计算粒子的适应度，通过比较当前的适应度值和适应度均值来判断如何改变惯性权重，利用式（8）进行改变，同时更新个体最优解和全局最优解。学习因子由式（9）和式（10）计算得到后，按式（2）和式（3）来更新每个粒子的速度和位置，根据式（11）对满足要求的粒子进行变异操作。

不断循环此步骤直到满足进化代数达到最大迭代次数或者全局最优解[Pgd]达到理想的改进精度，此时粒子的位置为更新后的位置。

4） 权值计算，將经过粒子群优化算法调整后的粒子取出。利用式（4）计算其权重，并且归一化权重。

5） 重采样，利用式（6）计算粒子的有效粒子数，若有效粒子数达不到阈值要求，则需要对粒子进行重采样以得到新的粒子集，新的粒子集权重均为[1N]。若有效粒子数大于阈值，则进行下一步。

6） 状态输出。

4  仿真分析

针对上述部分所提到的方法与步骤进行仿真分析。本文所进行的仿真实验都是在Matlab R2016a的环境下进行仿真。所选用的系统模型和状态模型表示为：

式中：rand（）为0～1的随机数;[R]为量测噪声方差;[Q]是过程噪声方差。

为了验证算法的性能，将标准粒子滤波算法（PF）、文献[9]调整惯性权重的粒子群优化粒子滤波算法（PSO?PF）和本文改进的自适应粒子群优化粒子滤波算法（APSO?PF）进行比较。比较的标准为均方误差（Mean?Square Error，MSE），其计算公式如下：

粒子数设定为50，迭代次数设置为100次，粒子的最大飞行速度设置为1 m/s，最大飞行距离设定为20 m。

PSO?PF算法中的惯性权重采用文献[9]所使用的方法进行变换，学习因子[c1]和[c2]均设定为2。

本文改进的APSO?PF算法中，惯性权重最大值和最小值[wmax]和[wmin]分别设定为0.9和0.4。惯性权重按照前面所提到的式（8）进行判断和改变。学习因子[c1]和[c2]按照式（9）和式（10）进行自适应变化，并进行变异操作。

在相同的情况下，对随机抽取的同一组粒子，分别使用粒子滤波算法、调整权重的粒子群优化粒子滤波算法和本文的改进算法对目标进行跟踪。图1，图2分别是量测噪声方差[R=1]、过程噪声方差[Q=1]和量测噪声方差[R=1]、过程噪声方差[Q=10]的情况下的跟踪效果图。

仿真图给出了粒子的真实值和各种方法得到的粒子状态值。通过仿真图可以看出，标准粒子滤波算法所得到的预测目标位置与真实目标位置相差较大，调整惯性权重的粒子群优化粒子滤波算法精度居中，而本文的改进算法能进一步提升目标跟踪的精度。在大部分情况下，改良算法都能较好地跟踪目标，其得到的目标位置大多都在真实位置附近，改良后的算法对目标的跟踪更为准确。

除此之外，对三种算法均方误差的计算中也可以验证改良算法的性能更好。其误差图如图3，图4所示。

从图3，图4中可以看出：标准粒子滤波算法的误差最大，调整惯性权重的粒子群优化粒子滤波算法的误差有明显减小，而本文改进的算法误差最小。

计算三种算法的均方误差，其结果如表1所示。

从仿真实验计算得到的平均值可以看出，本文改进的自适应粒子群优化粒子滤波算法得到的均方误差值最小。因此可以证实，对粒子滤波算法所提取的粒子利用改进的自适应粒子群优化算法进行位置调整，可以有效地提高算法的准确性。

5  结  语

本文在粒子群优化算法中引入自适应惯性权重以及学习因子，以减少基于粒子群优化的粒子滤波算法中出现局部寻优情况的可能性，同时，对移动后的粒子进行随机变异以提高多样性。仿真结果表明，改进后的基于自适应惯性权重和学习因子的粒子群优化粒子滤波算法能够减小跟踪误差，提高滤波性能。

参考文献

[1] GORDON N J， SALMOND D J， SMITH A F M. Novel approach to nonlinear/non?Gaussian Bayesian state estimation [J]. IEEE proceedings F： radar and signal processing， 1993， 140（2）： 107?113.

[2] 刘畅，杨锁昌，汪连栋.粒子滤波理论在单目标跟踪中的应用综述[J].飞航导弹，2017（10）：67?71.

[3] 昝孟恩，周航，韩丹，等.粒子滤波目标跟踪算法综述[J].计算机工程与应用，2019，55（5）：8?17.

[4] LI Min， CHEN Zhimei， SHAO Xuejuan. Iterated unscented Kalman particle filter algorithm based on a variable?step adaptive artificial fish swarm optimization [C]// 2016 35th Chinese Control Conference （CCC）. Chengdu， China： IEEE， 2016： 7050?7053.

[5] 方正，佟国峰，徐心和.基于粒子群优化的粒子滤波定位方法[J].控制理论与应用，2008，25（3）：533?537.

[6] ZHANG Liang， BAO Qilian， FAN Wenxiu， et al. An improved particle filter based on bird swarm algorithm [C]// 2017 10th International Symposium on Computational Intelligence and Design （ISCID）. Hangzhou， China： IEEE， 2017： 198?203.

[7] SUN Chengyuan， HOU Jian， SUN Wei， et al. An adaptive intelligent particle filter for state estimation [C]// 2017 36th Chinese Control Conference （CCC）. Dalian， China： IEEE， 2017： 7009?7014.

[8] 张才千，葛磊，韩东.基于目标跟踪的粒子群粒子滤波算法研究[J].计算机仿真，2014，31（8）：392?396.

[9] 刘峰，韩艳丽，王铎.自适应权重粒子群优化的粒子滤波算法[J].计算机仿真，2013，30（11）：330?333.

[10] KENNEDY J， EBERHART R， SHI Yuhui. Swarm intelligence [M]. San Francisco， USA： Morgan Kaufmann Publishers， 2001.

[11] 仝秋娟，赵岂，李萌.基于自适应动态改变的粒子群优化算法[J].微电子学与计算机，2019，36（2）：6?10.

[12] ARULAMPALAM M S， MASKELL S， GORDON N， et al. A tutorial on particle filters for online nonlinear/non?Gaussian Bayesian tracking [J]. IEEE transactions on signal processing， 2002， 50（2）： 174?188.

[13] 高国栋，林明，许兰.基于似然分布调整的粒子群优化粒子滤波新方法[J].计算机应用，2017，37（4）：980?985.

[14] 沈显君.自适应粒子群优化算法及其应用[M].北京：清华大学出版社，2015.