基于粘结滑移理论的钢纤维混凝土切口梁受弯性能研究

任 超，张昌锁，郝保钦，赵睿豪

（太原理工大学矿业工程学院，山西 太原 030024）

钢纤维混凝土（Steel Fiber Reinforced Concrete,SFRC）作为一种新型的复合材料，具有高韧性、高耐久性等优点，被广泛应用于建筑、道路、桥梁、隧道和军事工程等。国内有很多学者已对其有过研究。章四明[1]对7组SFRC试件进行了试验，研究了钢纤维含量对混凝土抗压强度和劈拉强度的影响。宋玉普等[2]对2种尺寸和6种钢纤维体积含量的试件进行了准静态多轴强度测试，结果表明纤维的最佳体积含量在1.0%～1.5%。SFRC是复合材料，成分复杂，内部构成材料具有随机性，是典型的非均质材料，其破坏过程和力学性能非常复杂，需要从细观层面进行分析以对SFRC性能有更准确的认识。力学试验研究只能观察宏观力学性能，而通过建立数值模型则可从细观层面开展研究。

国内外有很多的学者对SFRC开展过数值模拟研究。刘永胜[3]通过SPHB实验装置对SFRC进行了动静态力学试验，根据试验的应力应变曲线，提出了一种SFRC含损伤的本构模型。Qin Fang等[4]研究了新的SFRC三维数值模型在冲击和爆炸荷载作用下的动力响应和破坏模式。卞祝等[5]以SFRC试验为基础，分析SFRC梁的受剪性能，认为钢纤维的掺入有效抑制了斜裂缝的开展。张胜利[6]运用ABAQUS模拟了SFRC立方体的劈裂，但是该模型没有考虑钢纤维和混凝土之间的粘结滑移性能。

文章建立了不同钢纤维含量的SFRC梁三维细观有限元模型，通过与实验结果的对比分析，验证有限元模型的有效性，并进一步分析了纤维对SFRC梁弯拉性能及破坏模式的影响。

1 有限元模型的建立

建立SFRC数值模型时主要关注两个部分：一是SFRC几何模型的建立，二是钢纤维和混凝土之间力学关系的确定。文章建立的SFRC几何模型分为混凝土基体和随机定向分布钢纤维两个部分，钢纤维与基体间的粘结滑移关系通过单根纤维拉拔的数值模拟来确定，支座与SFRC之间摩擦系数设为0.5。SFRC有限元模型如图1所示。

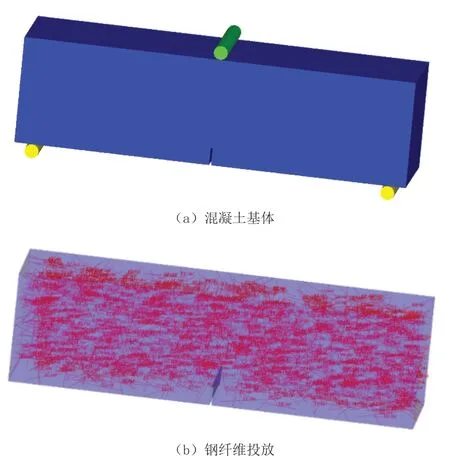
图1 钢纤维混凝土（SFRC）有限元模型

（1）本构模型。混凝土基体采用Karagozian & Case（K&C）模型，该模型优点是同时考虑了材料损伤效应、应变率增强和静水压力对屈服应力的影响。匡志平等[7]根据相关的试验研究成果，提出了一种确定K&C模型强度参数值的方法，并用LS-DYNA模拟爆炸荷载作用下钢筋混凝土板的动态响应，验证了K&C模型参数取值的正确性。张传爱等[8]运用K&C模型很好地预测了爆炸动荷载作用下钢筋混凝土构件的动态响应。文章结合试验数据与匡志平等提出的方法获取了适用于SFRC的K&C材料模型参数。纤维的材料模型采用LS-DYNA中的（MAT_024），通过赋予其一定的材料参数来模拟钢纤维和混凝土基体之间的粘结滑移关系。支座采用随动塑性强化模型，这种模型计算消耗较少，而且被广泛应用于模拟各种刚性材料的力学性能。所有材料参数如表1所示。

表1 材料参数

（2）材料失效准则和单元类型。文章的混凝土基体和支座均采用三维八节点实体单元，这种单元求解结果比较准确，节省时间，有利于克服材料非线性和单元大变形所造成的不收敛问题。但是这种单元在计算时要注意单点积分会带来LS-DYNA中的沙漏问题，模型设置沙漏系数为0.02。钢纤维采用Hughes-Liu积分梁。在Hypermesh中建立混凝土三维基体，为了节省计算时间和提高计算的精确性，混凝土基体设置网格尺寸为3mm，共划分单元458360个，上下支座共有单元1890个，SFRC共有单元460169个。

（3）三维钢纤维混凝土模型生成。钢纤维生成步骤：①用MATLAB中的混合同余算法生成随机数数列；②根据钢纤维的体积含量算出钢纤维的数量；③随机生成钢纤维位置和方向；④直接生成钢纤维的节点信息和编号，生成单元编号的k文件和节点的k文件；⑤将k文件导入Hypermesh软件生成钢纤维三维试样。钢纤维和混凝土之间的关系十分复杂，钢纤维在梁中切口位置主要是受拉，为了尽可能实现受拉作用，钢纤维和混凝土之间通过*CONSTRAINED_LAGRANGE_IN_SOLID作用相互连接在一起。

（4）钢纤维与混凝土之间的相互作用。通过单根纤维的拉拔来确定钢纤维和混凝土之间的粘结滑移作用。SFRC梁在受力过程中，主要因钢纤维拔出破坏，准确模拟SFRC梁破坏需要先获得钢纤维与基体之间粘结滑移参数。但是由于没有单根拉拔的试验，因此文章通过单根纤维的拉拔模拟来得到粘结滑移参数。

2 试验研究

为了验证所建立的三维细观模型的正确性，研究人员开展了SFRC切口梁三点弯曲试验，测定了钢纤维体积率为0.25%、0.4%、0.5%、0.6%的SFRC弯曲性能。

2.1 实验设计

该试验SFRC强度等级为C60，钢纤维采用贝卡尔特Dramix 4D纤维，钢纤维长度为62mm，直径为0.9mm，主要参数如表2所示。SFRC参数如表3所示。混凝土配合比如表4所示。其中，粗骨料是由花岗岩和石灰岩组成，其含水率分别为0.8%和1.5%。

表2 圆直钢纤维性质

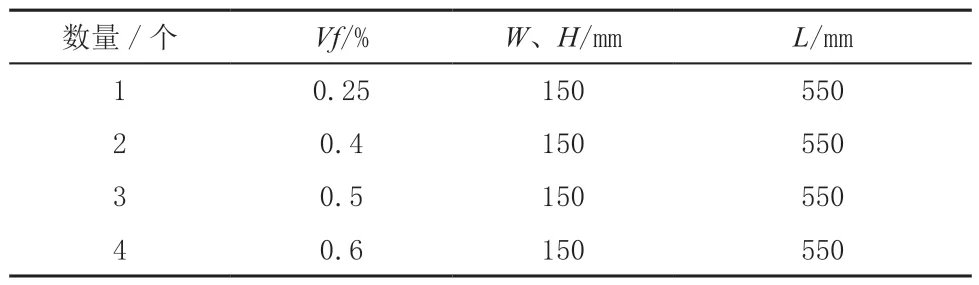
表3 SFRC试件参数

表4 混凝土配合比 单位：kg/m3

2.2 实验过程

试验采用《纤维混凝土试验方法标准》（CECS 13:2009）推荐方法，对不同纤维含量的棱柱体切口梁进行三点弯曲试验[9]。切口在小梁的中部，其深度为25±1mm，宽为3mm；梁跨距为500mm。试验布置图如图2所示。试验在最大承载力为100kN的伺服压力机上进行，采用开口位移控制加载速度方式加载。

图2 三点弯曲试验布置

2.3 试验结果

切口梁三点弯曲试验结束时试件状态如图3所示；得到荷载-开口位移曲线（F-CMOD）如图4所示；SFRC残余弯拉强度结果如表5所示。

图3 试验结果

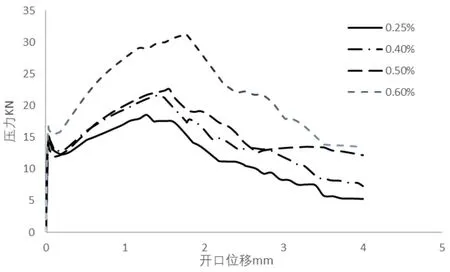
图4 钢纤维混凝土梁试验结果

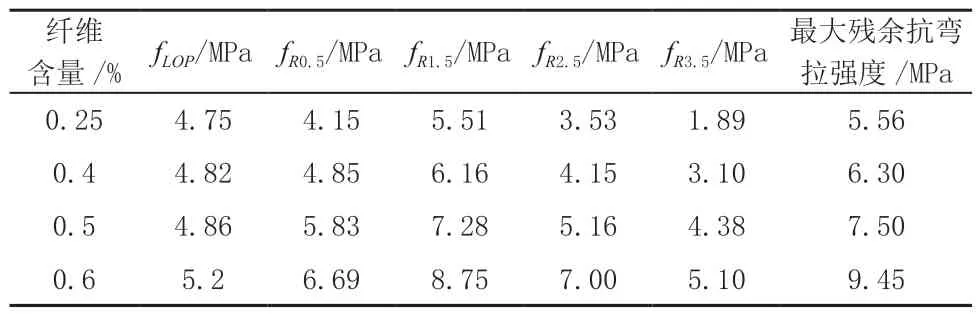
表5 三点抗弯试验的残余抗弯拉强度值

由表5可见，纤维含量为0.6%时，开口位移为3.5mm时的残余抗弯拉强度为5.10MPa，比0.5%含量的SFRC增大了16.44%，比0.4%含量的SFRC增大了64.52%，比0.25%的含量增大了169.84%。通过表5还可以发现，不同含量SFRC对应的最大残余抗弯拉强度不同，纤维含量越多，所对应的最大抗弯拉强度越高。纤维含量为0.6%的SFRC试件测得最大残余抗弯拉强度为9.45MPa，而0.25%的最大残余抗弯拉强度为5.56MPa，与前者相比降低了41.16%。

图4中含量为0.25%的SFRC梁，当荷载达到混凝土开裂荷载时，曲线进入急剧下降阶段，由于在切口梁处的钢纤维含量较少，不能够有效阻止混凝土梁的开裂，试件截面刚度的下降导致了试件承载能力下降。当其产生较大的变形后，钢纤维产生了较大的应力，并开始发挥作用，有效阻止了SFRC梁裂缝的进一步延伸；进一步施加荷载，梁继续发生变形，钢纤维的应力开始急剧增长，当应力值达到一个较高的水平之后，其影响已经大于混凝土梁开裂所产生的影响，导致荷载开始增大，展现出了应变硬化现象；继续施加压力，当钢纤维所受力大于纤维与基体间粘结滑移力时，钢纤维开始逐渐被拔出，曲线开始进入下降段。

当纤维含量大于0.5%时，由图4可见该含量的SFRC没有很明显的峰值荷载急剧下降段。由于含量为0.6%的SFRC梁中的钢纤维含量较多，在开裂时的荷载会明显高于素混凝土开裂时的峰值荷载，且由于钢纤维的含量较多，在梁的裂缝开始形成时，钢纤维就已经开始发挥作用，对裂缝控制起到积极作用，梁的刚度不会快速下降，因此挠度的变化也很小。由于较多钢纤维可提供更大的桥接应力，试件的承载能力在开裂后也缓慢地上升。同低掺量梁一样，当钢纤维所受力大于纤维与基体间粘结滑移力时，钢纤维开始被拔出，试件承载能力开始减弱，曲线开始进入下降段。

3 单根纤维拉拔模拟

单根钢纤维拉拔数值模拟可为SFRC梁模拟提供参数。模拟采用Wille等对单根钢纤维拉拔试验进行模拟校对，该试验中单根纤维直径和长度分别为0.2mm和13mm。试验中，纤维一半埋在混凝土中，另一半在外承受单轴拉力，如图5所示。当轴向位移等于6.5mm时，纤维即被完全拉出。该试验记录的轴力和拉出位移之间的关系，可供数值模拟校对使用。该次数值模拟采用单元删除方式来体现钢纤维和基体混凝土的分离，即当单元轴向应变（或等效塑性应变）达到一定值时（该值通过反复试算确定），删除钢纤维梁单元。

图5 纤维拉拔示意图

在数值模拟中，混凝土材料采用K&C模型，而钢纤维采用多段弹塑性模型。但需要特别强调的是，这里对材料模型中参数的取值并不是真正的材料属性，从数值模拟结果来看，如使用真正的材料属性（即高强钢参数）会使得预测的最大轴力过大。因此，该模拟的材料参数应通过反复调试取值，从而使得预测的轴向拉力和实验一致，实现对试验的较好模拟，如图6所示。事实上，纤维在受力过程中通常不会出现拉断现象，也就是说，该套参数反映了混凝土基体和纤维之间的粘结作用力，而不是真正的纤维材料属性。

图6 单根纤维拉拔试验与模拟的轴向应力对比

在三点或四点弯曲试验中，纤维通常是从埋深较短的一侧拔出的，因此对于13mm的钢纤维，其能抗拉拔的最大长度为13mm的一半，即6.5mm。但在多数情况下，钢纤维拔出长度应该小于6.5mm，如图7所示。按概率考虑纤维平均拔出长度应为6.5mm的一半，即3.25mm。

图7 埋深较短一侧的纤维被拔出

按照上述假定，计算拔出3.25mm钢纤维的轴向应力，考虑到纤维的拔出时轴向应力变化应与纤维埋深影响不大。由图6可见，对于埋深6.5mm的钢纤维，最大应力在1.1GPa左右，则埋深为3.25mm的钢纤维应力可按式（1）计算。

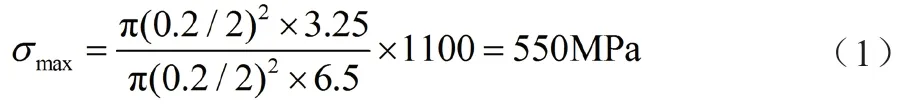
在三点弯曲或四点弯曲试验中，钢纤维应力随拔出深度的变化如图8所示。由图8可以看出，拔出3.25mm后，钢纤维应力降至0，较好地描述了不同钢纤维埋深的轴向应力变化过程。对于上述模拟和试验中的纤维在刚开始时应力状态为0，当开始拉拔纤维时，纤维的受拉的一端开始出现应力，呈现弹性变形阶段；之后应力上升到钢纤维发生塑性变形，最后导致破坏，纤维的应力开始下降；当纤维完全和混凝土发生脱粘，应力状态将下降到0。

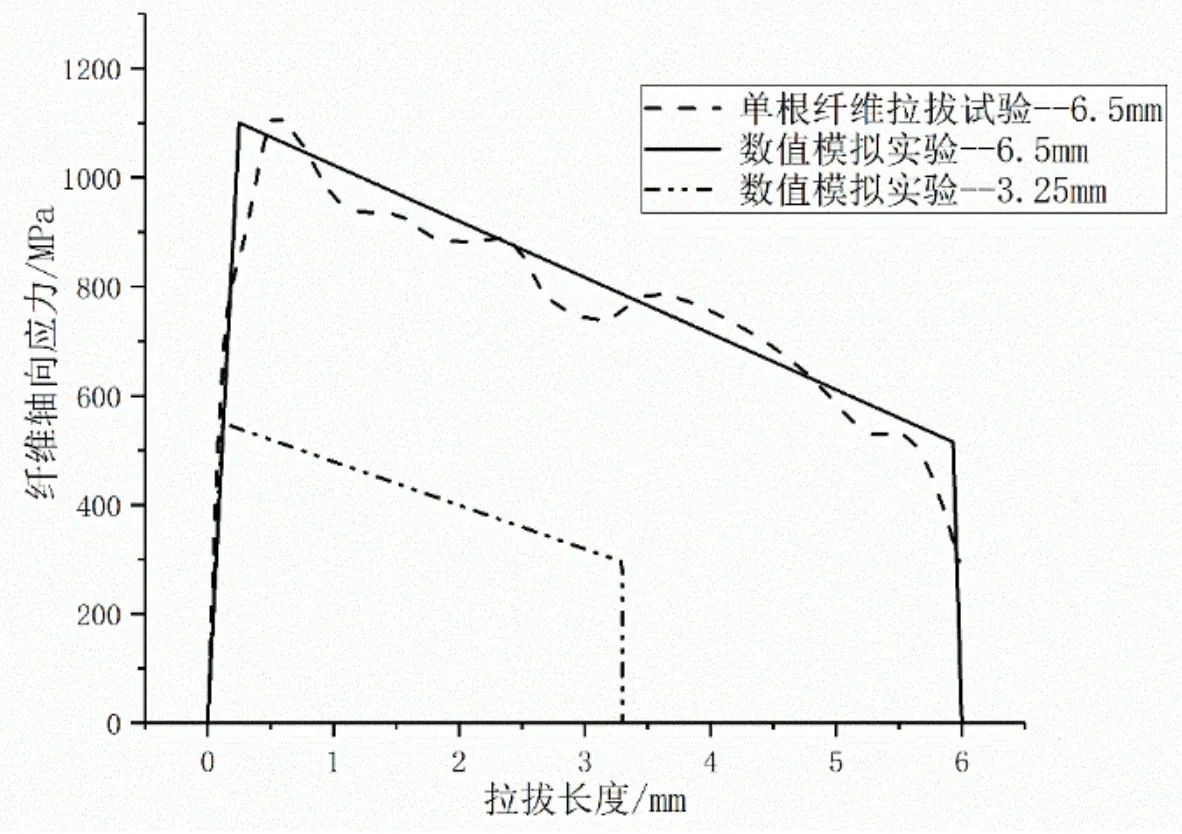
图8 试验中被拔出纤维的平均轴向应力曲线

4 三点梁模拟

将模拟得到的纤维与基体间粘结滑移参数应用于SFRC梁模型，模拟三点弯曲试验得到的所有模拟曲线如图9所示。由图9可见，当纤维的体积含量从0.25%提升到0.6%时，SFRC的最大峰值应力从17580N提升到31033N，最大峰值应力提升了76.5%，提升了混凝土的抗拉性能。从图9中还可以看出，当纤维含量低于0.6%时，钢纤维的含量对于混凝土初始的开裂并没有大的影响。而当纤维含量达到0.6%时，SFRC初裂强度明显增加。

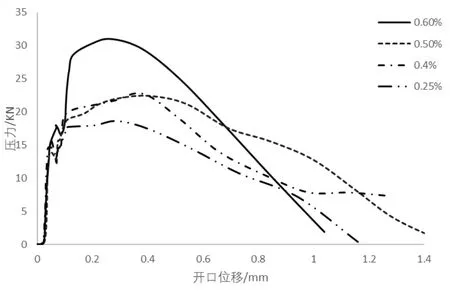
图9 钢纤维混凝土三点梁试验模拟结果

钢纤维混凝土三点梁试验结果与模拟对比如表6所示。根据表6可知，模拟可以较好地反映试验中三点梁抗弯拉时的峰值应力。在达到第一个峰值力以前，混凝土处于弹性阶段；第一个峰值力以后到第二个峰值力之间，混凝土开裂刚度下降曲线下行，之后钢纤维在其中开始受力，发挥作用；达到第三个峰值时，钢纤维受力被拔出，对混凝土基体产生破坏。由分析可见，利用宏观的混凝土与细观的钢纤维组成的二相复合材料的SFRC三维细观数值模型，可以很好地展现整个混凝土梁的受力过程，可以为以后SFRC梁的峰值力预测提供很好的参考。

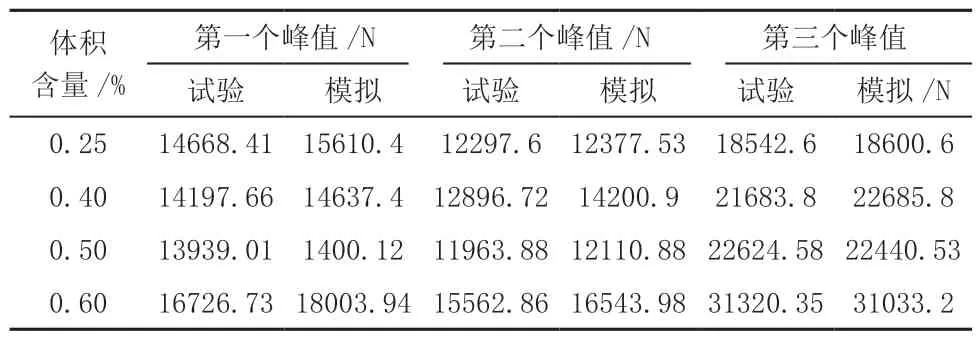
表6 钢纤维混凝土三点梁试验结果与模拟对比

5 结论

文章主要研究钢纤维混凝土的三点梁的抗弯拉性能，通过单根纤维的拉拔模拟确定了粘结滑移模型，并将其应用于SFRC三维细观尺度数值开展梁弯曲模拟。将模拟结果与试验结果进行了对比，可得出以下结论：

（1）不同的含量的SFRC切口梁在三点弯曲试验中F-CMOD曲线不同，随着纤维含量的增加，SFRC试件的承载能力增加。研究发现，纤维含量大于0.5%时，SFRC梁不会出现屈服阶段，发生应变硬化现象。

（2）采用MATLAB的编译得到在指定空间内钢纤维三维数值模型，能很好地反映钢纤维的随机分布特征，且生成的模型可以导入各种模拟软件中。

（3）采用单根纤维的拉拔模拟可得到符合钢纤维和混凝土粘结滑移性能的钢纤维的材料参数，方法可行，思路清晰。

（4）文章的SFRC梁数值模拟结果与试验中试件的强度结果较吻合，文章提出的方法可以较好地反映SFRC弯拉强度。