强震作用下大跨高墩桥梁伸缩缝处碰撞效应的参数研究
师新龙
(中建八局西南公司基础设施分公司,四川成都 610041))
随着我国西部地区的大发展,近年来在西部地区修建了大量的公路铁路桥梁。由于西部山区独特的地形地貌,为了适应地形,这些桥梁很多都采用了墩高超过40 m的高墩。据统计,已经建成和在建的公路、铁路桥梁中墩高超过40 m的达到了40 %以上[1]。而众所周知,西部地区是地震多发区,近年来就发生了汶川地震、芦山地震以及九寨沟地震等多次大地震。对这类高墩桥梁进行抗震性能研究[2],保证其地震安全能够为震后的抢险救灾提供快速通道,大大减少地震带来的生命财产损失。
对于这类高墩桥梁而言,其往往位于山区河谷地形,除了墩身高度较高,墩身质量大,高阶振型贡献大之外[3],另外一个问题就是其不规则性。为了适应地形,相邻的桥墩之间墩高都存在较大差异,有的相邻墩高差甚至高达几十米。相邻结构之间墩高的差异必将导致其刚度的迅速变化,从而使得相邻结构的动力特性也存在较大差异,地震作用下,高墩柔性结构和与之相邻的矮墩刚性结构之间容易发生严重的碰撞破坏,近年来不少学者都进行了相关研究。贾宏宇等人[2][4]采用随机振动理论研究了局部场地效应第不规则高墩桥梁碰撞间隙宽度需求的影响,结果表明空间变异的非一致场地可能会引起桥梁更为强烈的地震响应,从而增大桥梁的碰撞间隙宽度需求。洪浩等[5]研究了地震动相干效应对高墩桥梁地震响应的影响结果表明墩高差的存在反而有利于减小桥墩和主梁的截面内力。单德山等[6]人研究了不同断层距下高墩桥梁的地震响应,结果表明近断层地震作用下,高墩桥梁反应更为强烈。陈志伟等[7]研究了近断层脉冲效应对高墩桥梁地震响应的影响,结果表明近断层脉冲效应会显著增大桥梁的地震响应,相同的峰值加速度下,最大改变率可达到40 %。此外,为了考虑强震作用下,桥梁结构的混凝土开率,钢筋屈服支座破坏以及上部结构碰撞等非线性行为,李晰等[8]人分别研究了碰撞对高墩桥梁非线性地震响应的影响。康锐[9]采用易损性的方法,研究了碰撞效应对高墩桥梁抗震性能的影响。
以上研究虽然在一定程度上促进了我国高墩桥梁抗震设计理论的发展,然而在不规则高墩桥梁的抗震设计理论中还存在许多不足。本文将以西部地区某座典型的高墩桥梁为例,考虑碰撞过程中的能量耗散和刚度变化,详细研究支座刚度、碰撞间隙宽度、墩高差等因素对高墩桥梁非线性地震响应的影响,从而为高墩桥梁的抗震设计提供指导。
1 数值模型建立
以西南地区某高墩大跨连续刚构公路桥梁为依托,研究支座刚度、碰撞间隙宽度和墩高差等结构参数对高墩桥梁非线性地震响应的影响。桥梁跨径组成为(90+170+90)m,桥梁总长350 m,两个桥墩采用的是空心薄壁墩,墩高分别为116 m和126.06 m,墩身材料为C40混凝土。主梁为单箱单室预应力混凝土箱型梁,材料为C55预应力混凝土,梁截面高度由桥墩到跨中按照二次抛物线变化并在桥梁左右两端桥台处均设置了盆式橡胶支座(图1)。
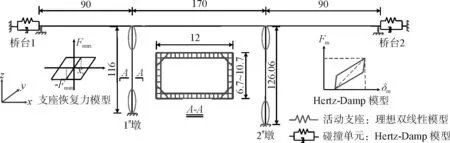
图1 三维有限元模型(单位:m)
参照桥梁设计资料,基于Open SEES平台建立桥梁三维非线性分析模型如图1所示。图1中主梁采用基于位移的梁柱单元(Displacement-based Beam-column Element,DBE)进行模拟,并通过节点两端赋予不同截面属性的方式模拟主梁的变截面。桥墩采用基于力的非线性梁柱单元(Force-based Beam-column Element,FBE)结合纤维截面来模拟强震作用下桥墩的非线性行为,支座采用零长度单元(Zero-Length Element,ZE)结合硬化材料(Harding Materials,HM)材料进行模拟。此外,图1同时还给出了桥墩横截面配筋示意图。由于螺旋箍筋的环箍效应,混凝土分为核心区混凝土和保护层混凝土两类,两种混凝土本构模型均采用Concrete02材料进行定义,本构模型均为Kent-Scott-Park模型[10]。钢筋采用Steel02进行定义,其本构模型采用Giuffré-Menegotto- Pinto模型[11]。
考虑到相邻主梁之间以及梁-桥台之间可能发生碰撞,在主梁两端桥台处分别设置了接触单元来模拟主梁与桥台之间的碰撞行为,本文采用Muthukumar[12]提出的简化Hertz-damp碰撞模型,其碰撞力-位移如图2所示。图2中δm为发生碰撞时的最大侵入位移;Fm为最大侵入位移对应的碰撞力;g为初始间隙;Keff为Hertz-damp简化模型等效刚度;K1和K2分别为初始刚度和应变硬化刚度。

图2 Hertz-Damp模型
模型中碰撞力的计算公式如下所示:
(1)
式中:c为阻尼系数,Kh为碰撞模型中的弹簧刚度系数,u1和u2为两结构的位移,gp为碰撞间隙宽度,n为Hertz系数,典型取1.5。
简化后Hertz-damp碰撞模型在碰撞过程中能量耗散的计算公式为:
(2)
式中:δm为最大入侵位移,e为恢复系数,通常取0.6~0.8。屈服位移δy常取最大入侵位移的0.1。
由简化碰撞模型与Hertz-damp模型的最大碰撞力相等,则简化碰撞模型的等效刚度为:
(3)
Kh为Hertz-damp模型的碰撞刚度,取值为结构的轴向刚度。等效刚度可以用初始刚度Kt1和应变强化刚度Kt2表示:
Keffδm=Kt1δy+Kt2(δm-δy)
(4)
简化碰撞模型的力与变形曲线所围成的面积As可以用Kt1、Kt2、δm表示:
As=(Kt1-Kt2)δy(δm-δy)
(5)
假设简化碰撞模型中力与变形曲线围成的面积近似等于结构碰撞过程中的能量耗散,可得到简化碰撞模型的刚度参数K1和K2。
(6)
(7)
式中:a为屈服系数;ΔE为碰撞过程中的能量耗散,其详细计算过程见文献[12]。
2 地震记录选取
在选择地震记录时,本文首先采用30 m土层平均剪切波速量化局部场地条件,然后以JTG/TB02-01-2008《公路桥梁抗震设计细则》[13]中的设计反应谱作为目标谱,采用谱兼容[14-15]的方法从PEER选择天然地震记录。所选地震动反应谱与目标谱的匹配程度采用均方误差MSE来衡量,MSE按照式(8)进行计算。
(8)
式中:SAtarget(Ti)为目标反应谱,可按照JTG/TB 02-01-2008《公路桥梁抗震设计细则》[14]确定;SArecord(Ti)为所选地震动反应谱;Sf为调幅系数;w(Ti)为关注周期段内的权重函数。为了考虑地震动的不确定性,按照JTG/TB02-01-2008《公路桥梁抗震设计细则》的要求选择了七条天然地震记录,其详细信息见表1,地震动记录反应谱与目标谱匹配情况如图3所示。从表1可以看出,所选地震动反应谱与目标谱的均方误差MSE非常小,其值都在0.07~0.14之间,说明在感兴趣的周期段内所选地震动反应谱与目标谱较为匹配。

表1 地震记录信息

图3 所选地震动反应谱与目标谱的比较
此外,从图3中也可以看出,虽然在感兴趣的频段内,所选地震动反应谱与目标谱较为匹配,但是二者同样也存在一定差异,这说明所选地震动能够在一定程度上反应地震动的不确定性。
3 非线性地震响应参数分析
将表1中所选地震动记录分别乘以调幅系数,然后作为激励施加到上述非线性有限元模型,采用牛顿迭代的方法对其动力响应进行求解,从而获得桥梁结构非线性地震响应。为研究碰撞刚度、支座刚度、碰撞间隙宽度及墩高差对桥梁结构地震响应的影响,算例中求得表1中7条地震激励的峰值响应,并取7条地震动峰值响应的平均值作为结构地震响应的指标。本文墩高差主要体现在等墩高与不等墩高两个方面。
3.1 梁端碰撞间隙宽度的影响
考虑碰撞间隙宽度从0.05 m变化到0.15 m,图4给出了地震作用下2个桥墩的非线性地震反应峰值随碰撞间隙宽度的变化曲线。从图4可以看出:地震作用下1号墩的墩底曲率和墩顶位移都明显要更大些,但墩底弯矩明显要更小。因此,对于不规则高墩大跨连续刚构桥,地震作用下矮墩的变形需求更大,而高墩的内力需求更大。产生这种现象的原因主要是由于2号墩墩高较高,墩身质量更大,结构自振周期较长,地震作用下高阶振型对其影响较大,从而导致了其变形较小而内力较大。
随着碰撞间隙宽度增大,1号墩与2号墩的墩底曲率、墩顶相对位移峰值都出现递增的规律,但弯矩内力略有差异。碰撞间隙宽度越大,1号墩与2号墩的墩底曲率差别越大,二者之间最大相差约1.24倍。不同的碰撞间隙宽度下,1号墩的墩底曲率、墩顶相对位移的最大差异分别达到了2.37倍与0.77倍,2号墩的墩底曲率、墩顶相对位移最大差异分别达到了1.79倍和0.77倍。
从图4还可以看出,1号墩与2号墩的墩底弯矩随碰撞间隙宽度增大呈现出对称分布的规律。1号墩的弯矩内力随碰撞间隙宽度呈增→减→增的变化趋势,2号墩却与之相反,但都在碰撞间隙宽度为10 cm时,弯矩内力达到了峰值,两者峰值之间相差约7.2 %。不同的碰撞间隙宽度下,1号墩、2号墩弯矩内力的差异分别达到了2.2 %与1.5 %。
不同的碰撞间隙宽度会对桥梁结构的内力、位移、曲率等地震反应产生极大影响,其次伸缩缝的不同取值对墩底曲率、墩顶位移的影响程度更大些。因此,设置一个合理的碰撞间隙宽度取值有利于减小墩顶位移,降低墩底的损伤程度,也使梁端发生碰撞的几率大大减小。

(a)墩底曲率
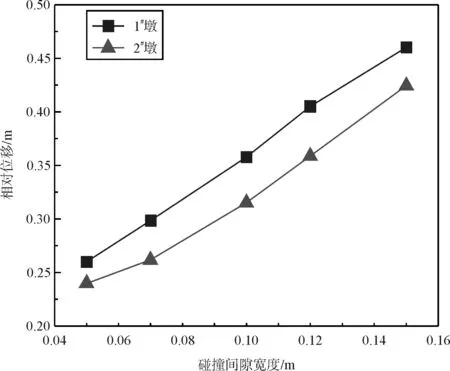
(b)墩顶相对位移

(c)墩底弯矩图4 碰撞间隙宽度参数分析
3.2 梁端碰撞刚度的影响
图5给出了不同的碰撞刚度参数对桥墩非线性地震响应的影响规律。从图5(a)、图5(b)分析可知:随着碰撞刚度的增大,1号墩与2号墩的墩底曲率、墩顶相对位移都在减小,且碰撞刚度越大,减小地越缓慢。在碰撞刚度系数为0.6时,1号墩与2号墩的墩底曲率、墩顶相对位移都达到了最大值,墩底曲率最大相差约76 %,墩顶相对位移最大相差约17.4 %。在不同的碰撞刚度下,1号墩的墩底曲率、墩顶相对位移的最大差异分别达到了1.45倍与0.77倍,2号墩的墩底曲率、墩顶相对位移的最大差异分别达到了1.66倍与0.86倍。

(a)墩底曲率

(b)墩顶相对位移
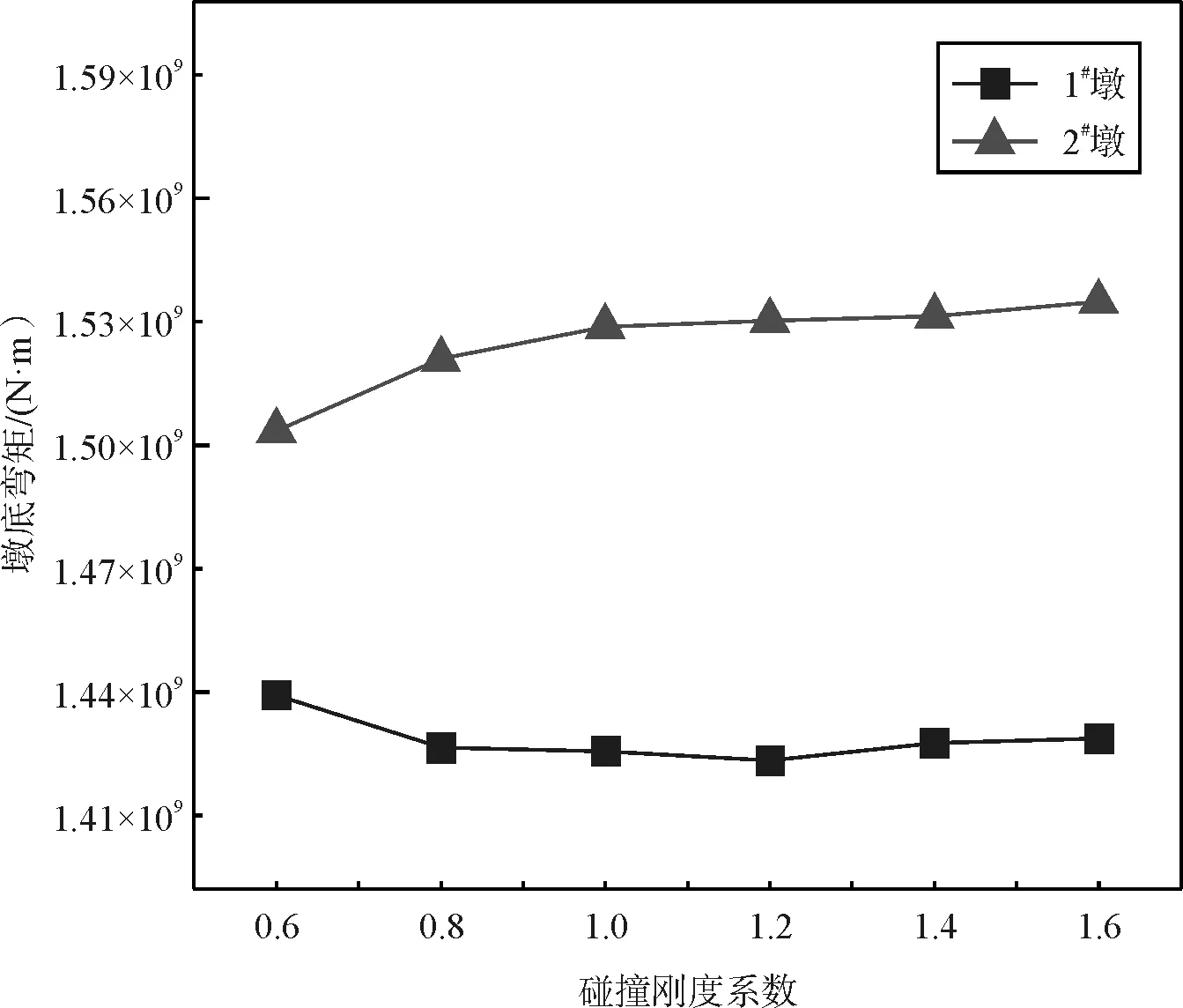
(c)墩底弯矩图5 碰撞刚度参数分析
从图5(c)可以看出:1号墩与2号墩的墩底弯矩变化规律截然相反。在碰撞刚度系数为0.6时,1号墩的弯矩内力达到了最大峰值,在碰撞刚度系数为1.6时,2号墩的弯矩内力达到了最大峰值,其中1号墩与2号墩的墩底弯矩最大相差约7.4 %。除此之外,在不同的碰撞刚度下,1号墩的墩底弯矩最大差异约为1.1 %,2号墩的墩底弯矩最大差异约为2.1 %。不同的碰撞刚度取值对位移、曲率的影响远大于内力响应的影响,且对高墩的影响更大。
3.3 墩高差的影响
为研究墩高差对桥梁结构碰撞响应的影响,本文将1号墩加长10.06 m使之与2号墩等高,为此建立等墩高与不等墩高的弹塑性动力分析模型,在此基础上进行进行桥梁结构非线性地震响应分析,图6给出了墩高差对桥梁结构墩底曲率、墩顶相对位移、墩底弯矩等碰撞响应的分析图。
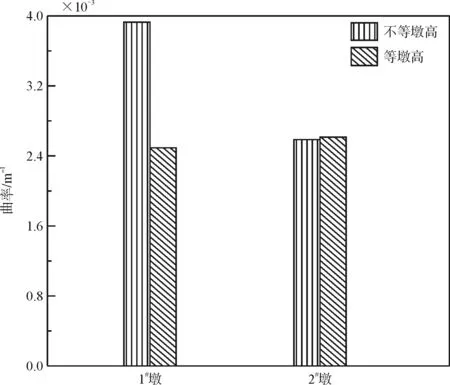
(a)墩底曲率

(b)墩顶相对位移

(c)墩底弯矩图6 墩高差碰撞响应对比
从图6(a)可以看出,墩高差对1号墩的墩底曲率影响程度明显要大于2号墩,对于1号墩,相比等墩高模型,不等墩高时的墩底曲率要大57 %左右。对于2号墩,等墩高时的墩底曲率却稍大些。从图6(b)分析可知:对于1号墩和2号墩,相比不等墩高模型,等墩高模型的墩顶相对位移要大1.8 %左右。从图6(c)可以看出,墩底弯矩随墩高差的变化规律与墩顶相对位移的变化规律相一致。对于1号墩,相比不等墩高模型,等墩高模型的墩底弯矩要大3.5 %,对于2号墩,等墩高模型的墩底弯矩仅比不等墩高模型的墩底弯矩大0.85 %。
因此,对于山区不规则高墩桥梁,在考虑主梁与桥台的碰撞作用后,主墩之间存在墩高差会对桥梁结构的地震响应产生极大差异。相比等墩高模型,主墩之间存在墩高差对墩底曲率的影响更大,对其具有一定的放大效应,尤其对矮墩的放大效应更明显,相应的墩底弯矩与墩顶位移却有所减小。说明设置一个合理的墩高差有利于减小梁端碰撞作用下桥墩的变形与内力响应,从而降低桥墩的损伤状态,这对桥梁结构的抗震设计非常重要。
4 结论
本文基于OpenSees软件建立了山区高墩连续刚构桥的非线性有限元模型,充分考虑强震作用下桥梁结构的材料非线性以及主梁在碰撞过程中的能量耗散和刚度变化。详细研究了高墩桥梁的碰撞效应对其桥墩非线性地震响应的影响。主要得出如下结论:
(1)不同的碰撞间隙宽度会对桥梁结构的碰撞响应产生极大差异。其中碰撞间隙宽度从5~15 cm变化时,1号墩(矮墩)的墩底曲率、墩顶相对位移的最大差异分别到了2.37倍与0.77倍,而弯矩内力的差异仅有2.2 %;当存在墩高差时,碰撞间隙宽度的不同取值对矮墩的影响程度更大,对内力响应的影响要明显小于对位移、曲率等地震响应的影响。因此,在考虑了梁端碰撞效应后,采用曲率作为桥墩的损伤指标更能够合理地反映桥墩的损伤状态。
(2)强震作用下,桥台与主梁之间的碰撞刚度越大,相应的墩底曲率、墩顶相对位移越小。在碰撞刚度系数从0.6~1.6变化时,2号墩(高墩)的墩底曲率、墩顶相对位移的最大差异分别到了1.66倍与0.86倍,而弯矩内力的差异仅为2.1 %。不同的碰撞刚度对墩顶位移、墩底曲率的影响远大于对内力响应的影响,尤其对于较高的墩其影响要更大些。
(3)墩高之间的差异性对墩底曲率具有一定的放大效应,且对1号墩(矮墩)的放大效应更明显,其墩底曲率放大约57 %,而墩顶相对位移、墩底弯矩分别减小约1.8 %与3.5 %,因此,墩高差的存在在一定程度上会降低桥梁墩底的内力,减小梁端发生碰撞的几率。

