保温原油管道蜡沉积速率模型的建立

孙启智，刘 祁，郎宪明，胡志勇

（1. 辽宁石油化工大学 石油天然气工程学院，辽宁 抚顺113001；2. 中国石油管道公司 沈阳调度中心，辽宁 沈阳110000；3. 辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺113001）

我国原油管道分布范围广，输送的原油大都具有高凝点、高含蜡的特性[1]。管道输送过程中，由于油壁温差的存在，油温会逐渐降低，油品中的蜡结晶析出，通过剪切弥散等作用附着在管道内壁，形成蜡层[2]。从经济角度看，由于蜡层厚度不断增加，管道的当量直径持续变小，输量也会相应减少，严重时在蜡层较厚的位置易发生凝管事故[3⁃4]。管道中的蜡随着时间的推移逐渐增多，间接地起到了保温的作用，降低了热力费用，与此同时，管道的流通面积减小，动力费用增加[5⁃6]。因此，对蜡沉积速率进行科学的预测研究，减少在实际管线中的经济损失尤为重要。

20 世纪国内外学者开始对蜡沉积速率模型进行研究。E.D.Burger 等[7]简单地叠加了分子扩散和剪切弥散作用建立了蜡沉积速率模型，忽略了油品中的蜡晶分子并不是全部沉积到管壁处，结果误差较大。J.Hun 等[8]定义了临界蜡强度概念，引入了蜡沉积倾向系数，创建了蜡沉积速率模型，该模型未考虑实际管线中复杂的运行状况，结果与实际情况误差较大。汪继峰[9]通过定义蜡沉积势，利用Fick扩散定律得到蜡沉积速率表达式。该模型只考虑到流动决定沉积层结构状态，而对蜡沉积的传质过程没有影响，不满足实际管线的情况，故该模型不适用。黄启玉等[10]通过室内实验确定蜡沉积系数、剪切应力和管壁温度梯度的关系，该模型可以计算不同工况下的蜡沉积速率。

本文在前人研究的基础上，考虑到影响蜡沉积速率的4 个因素：油品黏度、管壁处温度梯度、管壁处的剪切应力和管壁处蜡分子浓度梯度，建立了逐步回归模型和支持向量机模型。通过室内环道实验对两种模型进行对比分析，并对现场蜡沉积速率进行预测。

1 蜡沉积速率模型

1.1 逐步回归模型

逐步回归是处理自变量与因变量间的常用手段之一，它可以获得隐藏在背后的统计规律，通过计算得到回归方程。在计算过程中，通过显著性检验引入变量，去除其中不显著的变量，直至没有新的变量可以引入到方程中，最后建立多元线性回归方 程[11⁃12]。

蜡沉积速率模型是一个多元非线性模型，首先对方程进行线性化处理[13⁃14]；然后通过线性回归，对方程进行回归分析。一般以指数幂的积的方程进行线性化处理，以二元幂函数方程为例:

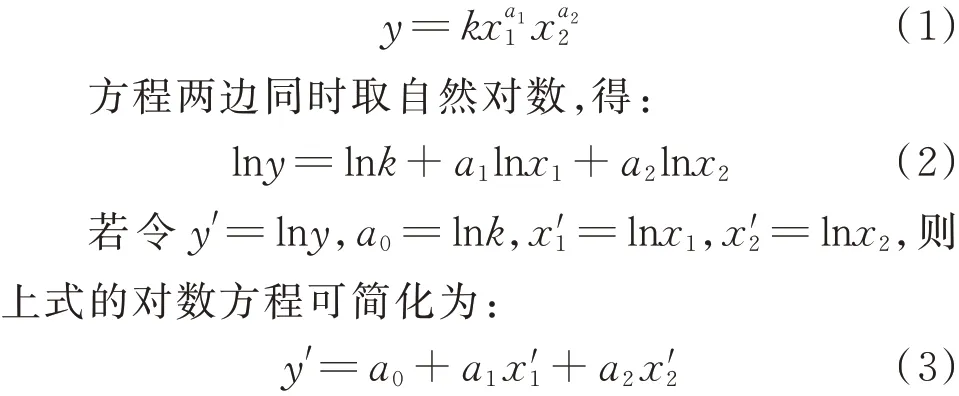
a0、a1、a2的值即是所求回归方程（1）中的回归系数k = exp( a0)，a1、a2的值。

多元幂函数方程的回归与二元幂函数方程的回归所用方法相同，也可以根据上述方法将方程进行变换，用线性回归方法求出线性方程的系数，从而求出多元方程的各个系数的值。

1.2 支持向量机模型

支持向量机法通过结构风险最小化原理提高泛化能力，具有从大量的信息中自动识别并提取关键信息的特点，适合解决多元非线性回归问题。通过对典型空间的描述，得出因子群与预报对象的关系，是一种适合于小样本的学习机器[15]。

1.2.1 支持向量机原理 支持向量回归机是由支持向量理论发展的一种回归技术，在回归算法中展现了很好的性能，在诸多领域上已得到应用。

（1）线性支持向量回归机。 样本数据T ={( x1,y1),…,( xi,yi)} ∈( x,y )l，其 中 第i 个 输 入 数 据xi∈Rn，yi∈R。回归方程为f ( x) = w ⋅x + b，其中w ∈Rn，x ∈Rn，⋅ 表示内积运算，b ∈R 是偏置。将线性回归问题变成优化问题：

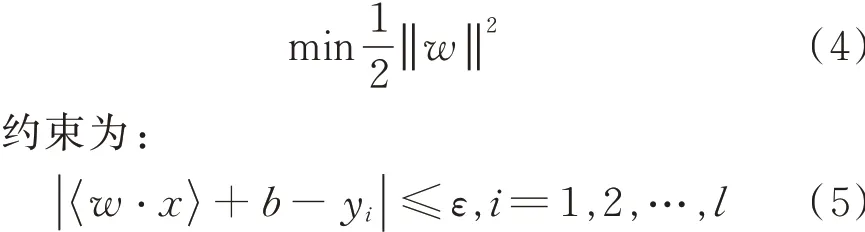
一般情况，针对二次规划问题，常常求解它的Lagrange 对偶问题。选择损失函数为ε，不敏感损失 函 数 c( x,y,f ( x ))=| y - f ( x ) |ε，其 中| y -f ( x ) |ε= max { 0,| y - f ( x ) | - ε }，这里的ε 是一个正数，支持向量的个数可以通过控制ε 的值来确定。为此，引入Langrange 函数：

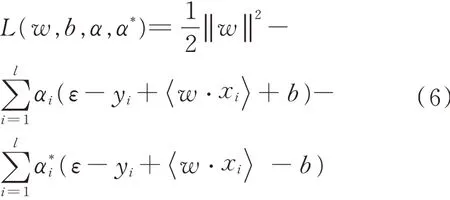
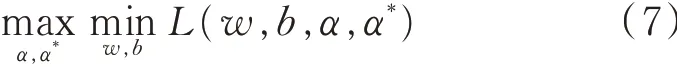
利用kuhn⁃tucker 条件，函数L 的极值应满足条件：

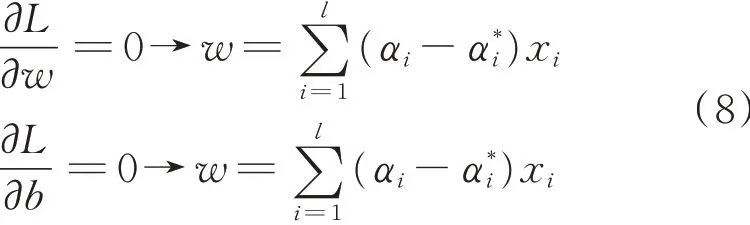
于是得到原优化问题的对偶形式：

其中，（αi- α*i）不等于零对应的样本数据就是支持向量。 b 的计算，由非线性规划的KKT 条件可以得到：

（2）非线性支持向量回归机。 对于非线性回归，首先使用一个非线性映射φ( ⋅)将样本的输入xi由输入空间X映射到一个高维特征空间H，利用这个特征空间H构造出线性支持向量回归机。此时，高维特征空间中的线性回归问题对应了低维输入空间的非线性回归问题，避免了维数灾难。

另外，考虑到可能存在误差，引入两个松弛变量：ξi,ξ*i≥0,i= 1,2,…,l

优化为：

约束条件为：

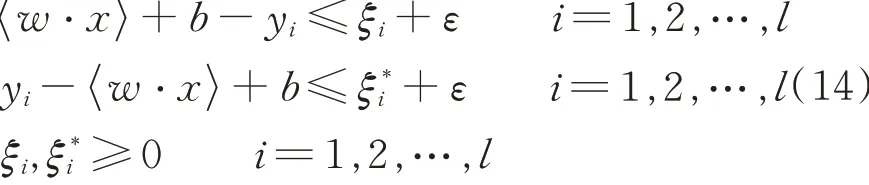
式中，为松弛因子，目标函数的第一项使函数更为平坦，提高了泛化能力；第二项减少了经验风险。 为了求解这个二次规划问题，引入Lagrange函数：

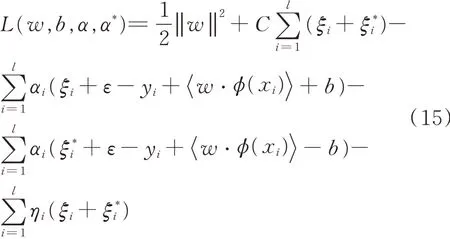
其中，αi,α*i≥0,i= 1,2,…,l，C用于控制模型的复杂度和逼近误差的折中，越大则对数据的拟合程度越高；ε用于控制回归逼近误差和模型的泛化能力。

函数L的极值应满足条件：

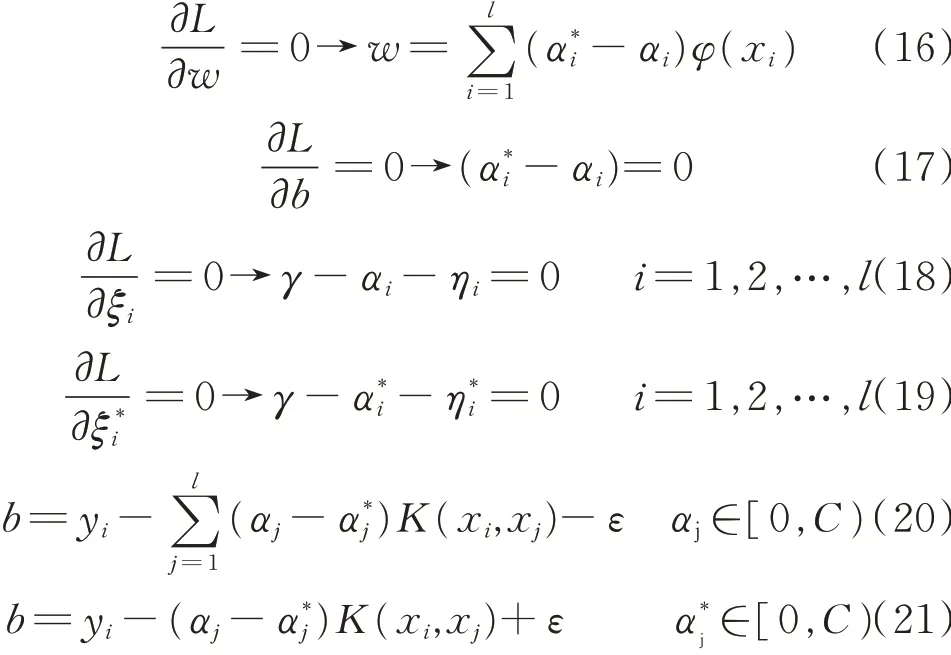
于是得到原优化问题的Lagrange 对偶问题为：

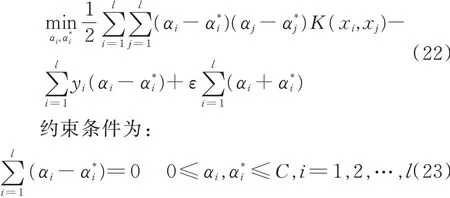
1.2.2 支持向量机模型预测步骤 利用MAT⁃LAB 的支持向量机工具箱可以用于预测室内和现场的蜡沉积速率，其具体步骤为:

（1）建立学习样本和测试样本：基于蜡沉积环道实验数据，以管壁处剪切应力、管壁处温度梯度、管壁处蜡分子浓度梯度这4 个影响因素作为输入向量，以蜡沉积速率为输出向量。

（2）数据的导入和预处理：对读入的数据进行预处理，预处理的目的主要是可以加快训练速度。所用的函数为prested 归一化函数。

（3）核函数的选择：核函数有不同的形式，常用的有线型核、多项式核、径向基核（RBF）等，RBF 核只有一个待定参数，拟合精度较高，文中选择RBF 核。

（4）支持向量机的参数设置：c1=c2= 0.1，其中最 速 下 降 法 的 参 数μ= 0.01，σ= 0.01，误 差 要 求epsilon = 1× 10-5，迭代次数为100 次。

（5）训练建立模型：利用支持向量机对学习样本进行样本学习，得到输入输出参数的关系，训练结束后即可得到支持向量和偏差量。

（6）测试样本预测：导入预测数据，预处理后利用建立的模型对测试样本进行预测，并分析其预测的精度。

2 蜡沉积实验

2.1 蜡沉积室内实验

实验装置如图1 所示。

图1 保温管道蜡沉积实验装置Fig.1 Insulation crude oil pipeline wax deposition experimental device

实验中使用的是改进的保温原油管道蜡沉积实验装置，装置主要由储油罐、循环罐、管道（包括测试管段、参比管段以及连接管）、控温系统、动力系统、温度、压力及流量测量系统等组成，

实验所用原油为庆吉混油，流量选择1.30、1.40、1.50 m3/h，油温选择34、36、38、40、42、44 ℃，油壁温差选择2、4、6 ℃。实验中根据需要，在上述范围内选择不同的流量、油温和油壁温差组合，形成共54 组实验方案。

2.2 蜡沉积室内实验结果

通过室内环道实验，得出不同条件下的蜡沉积速率，利用SPSS 软件回归出逐步回归模型，见式（25）。利用MATLAB 软件得到支持向量机模型。选择其中36 组作为学习组，18 组做为验证组。观察两种模型准确度，结果如表1 所示。

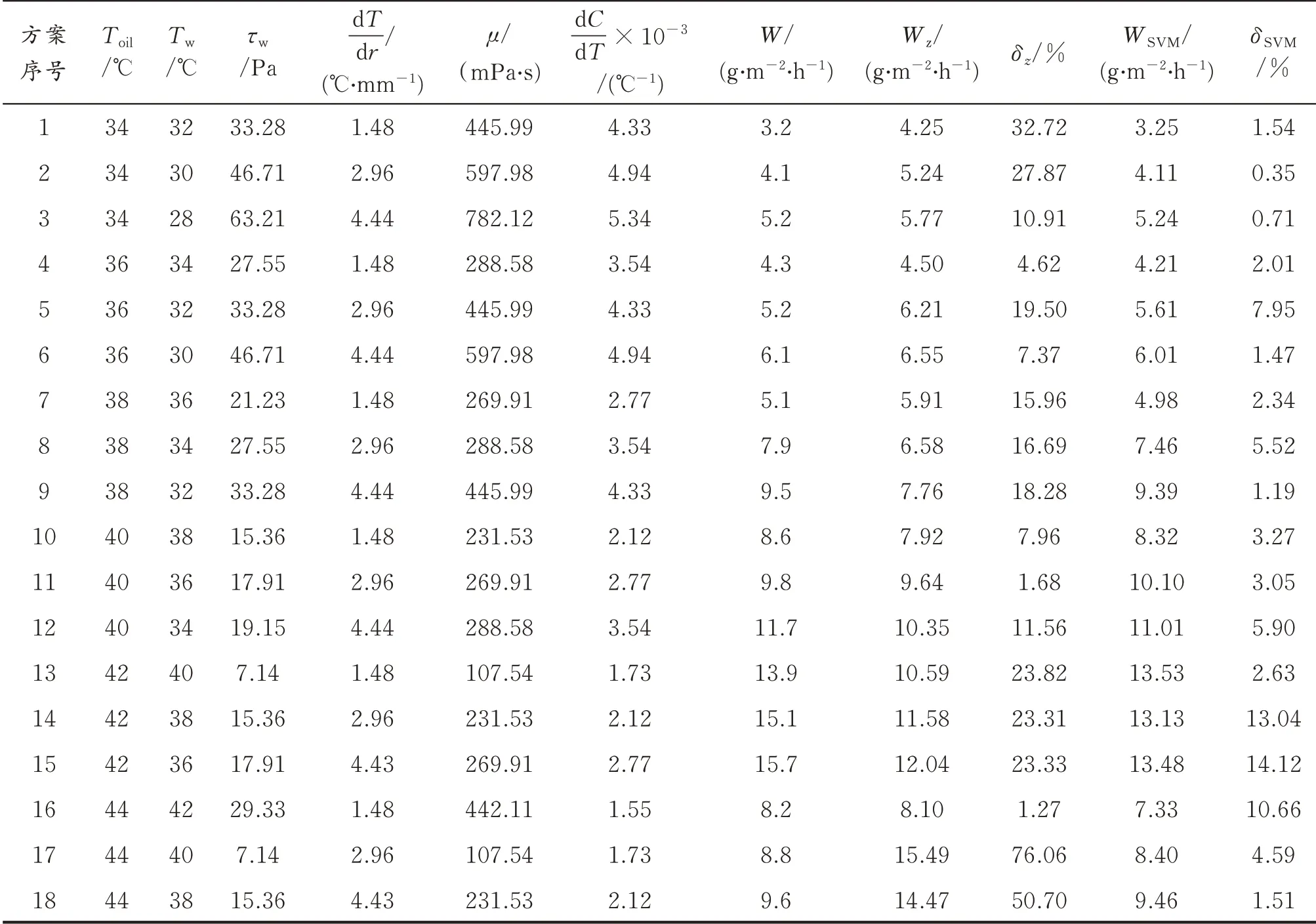
表1 实验值与两种模型预测值的相对误差Table 1 Relative error between experimental values and predicted values of two models

表1 中，Toil为油温；Tw为壁温；τw为壁面剪切应力，dT/dr为径向温度梯度，μ为动力黏度，dC/dT为蜡分子浓度梯度；Wz为逐步回归模型预测的蜡沉积速率；WSVM为支持向量机模型预测的蜡沉积速率；δz为Wz与W的相对误差；δSVM为WSVM与W的相对误差。

由表1 可知，逐步回归模型预测结果误差最大值达到了76.06%，最小值为1.27%，平均误差为20.76%。支持向量机法预测值在稳定性和准确度皆优于逐步回归法，误差最大值为14.12%，最小值为0.35%，平均误差为4.55%。综合比较，在室内实验中支持向量机模型优于逐步回归模型。表1 数据得出模型值与实际值的蜡沉积速率对比，结果如图2 所示。

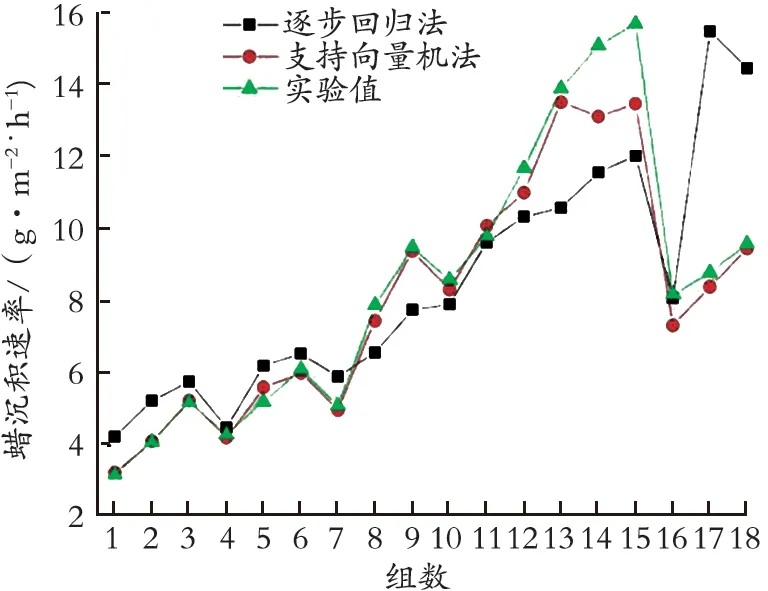
图2 室内实验蜡沉积速率对比Fig.2 Contrast diagram of wax deposition rate

由图2 可知，支持向量机法预测值和实验值的吻合程度较高，逐步回归模型计算的数据与实际值略有差距。

2.3 因素分析

2.3.1 极差分析法 影响蜡沉积速率包括流量、油壁温差和油温，为了找出主次影响因素，采用极差分析法对以上数据进行分析[16]。各个因素计算得出的极差不相等，说明各个因素对实验结果的影响程度不同。极差越大，说明该因素对实验结果的影响越大[17]，分析结果如表2 所示。

由表2可知，影响庆吉混油蜡沉积速率最大的是油温，其次是油壁温差，最后是流速。

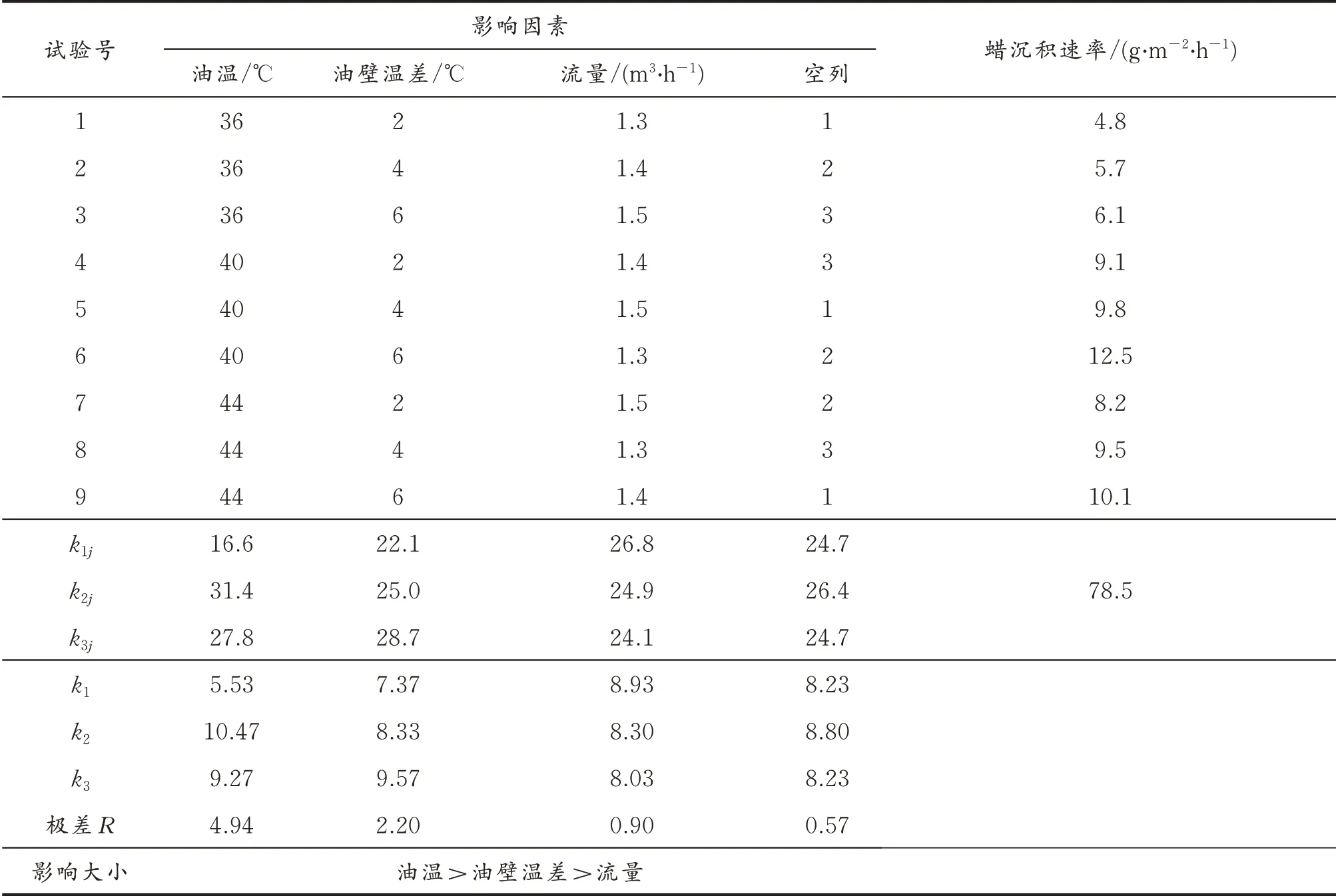
表2 室内实验极差分析Table 2 Range analysis results of laboratory tests

2.3.2 方差分析法 方差分析法实际上是把数据的总变异分为两个部分，分别为各因素引起的变异和误差引起的变异，由此构造出F统计量，作F检验，从而对各因素的显著性进行判断[18]。

总偏差平方和总自由度，计算公式为：

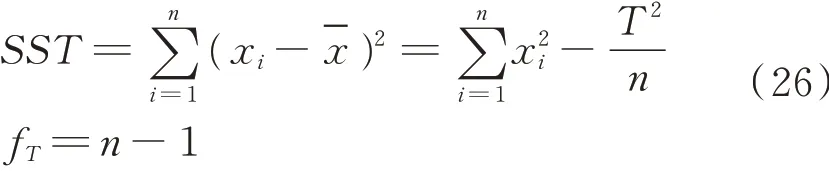
各列偏差平方和与自由度：

经过计算，室内实验方差分析结果如表3所示。由表3 可知，影响庆吉混油蜡沉积速率最大的是油温，其次是油壁温差，最后是流量。

表3 室内实验方差分析Table 3 Variance analysis results of laboratory tests

2.4 现场预测

图3 为利用两种模型对松山⁃葫芦岛保温原油管段进行春秋、夏和冬季蜡沉积速率的预测。

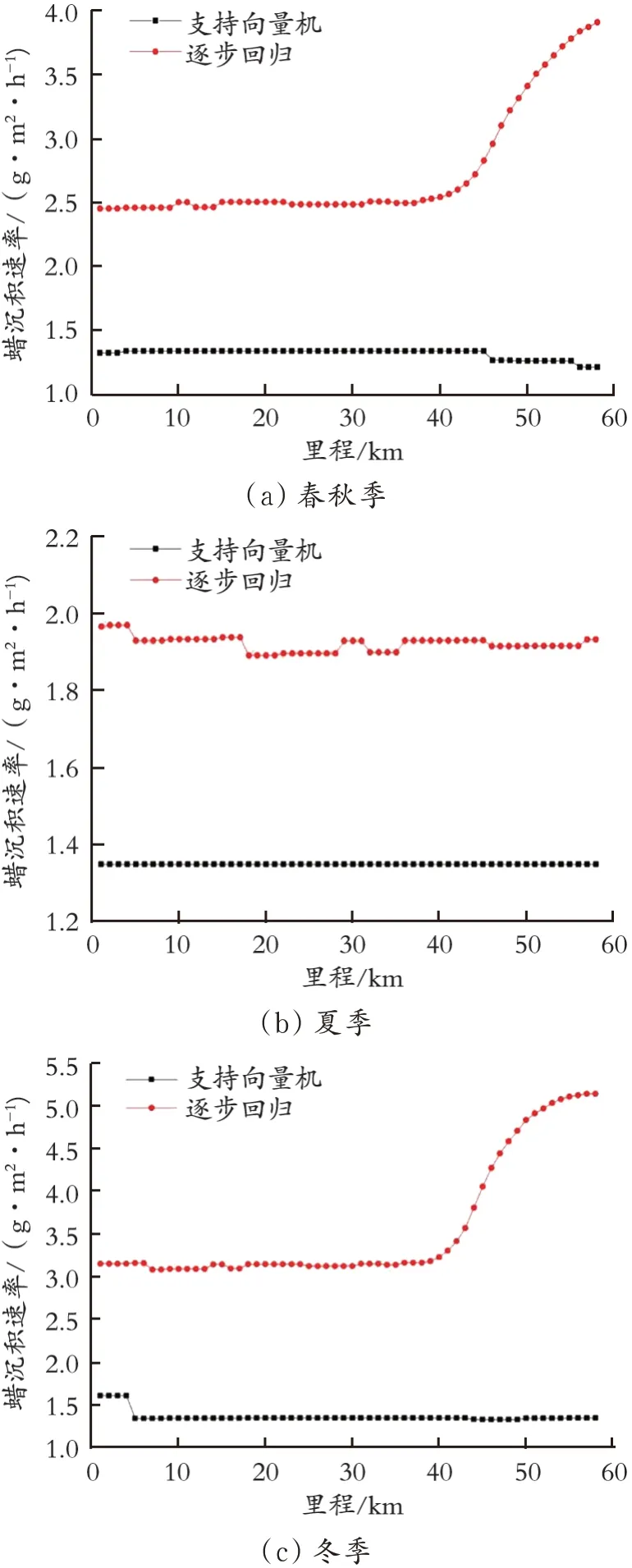
图3 预测管道沿线蜡沉积速率变化Fig.3 Prediction of wax deposition rate along pipeline

由图3（a）可知，油品在管道前段和中间段处于牛顿流体阶段，蜡沉积速率处于平稳期。随着运行距离的增加，由于管壁温差的存在，油品温度降低，在管道后段油品温度处于析蜡高峰期，蜡晶分子大量析出，在剪切弥散等作用下吸附在管壁处形成蜡层。可以得出，逐步回归法可以很好地预测这种趋势，但支持向量机法预测结果稳定在一个定值左右，不能预测各个位置管段的蜡沉积厚度。

由图3（b）可知，由于地温较高，管壁处的油壁温差较小，沿程热量散失也较少，油品在管道的温降很小，管道内油品一直处于反常点之上，油品处于牛顿湍流状态，蜡沉积速率没有很大变化。可以得出，逐步回归法和支持向量机法预测的蜡沉积速率值基本处于一个固定值，没有很大的浮动。

由图3（c）可知，地温为全年最低，油壁温差较大，油品在管道的降温速度较快。 在管道的前中段，油品蜡沉积速率处于稳定时期，随着运行距离的增加，在管道后段，油品温度进入析蜡高峰期，蜡沉积速率增大。可以得出，逐步回归法可以很好地预测这种趋势，但支持向量机法不可以，支持向量机法预测值基本不变。

综合以上分析，逐步回归法预测值明显高于支持向量机法，且可以很好地预测管段各个位置的蜡沉积速率，而支持向量机法不具备预测这种趋势的能力。管线在冬季的蜡沉积速率最大，夏季最小，这是由于冬季的地温最低，管壁处的油壁温差较大，沿程热量损失较多，油品的黏度逐渐增大，说明油壁温差是影响蜡沉积速率的主要因素。

3 结论与建议

根据蜡沉积产生机理，建立了预测蜡沉积速率的逐步回归模型和支持向量机模型，为验证模型精度，建立了室内环道实验装置，分别对两种模型进行了检验，并对松山⁃葫芦岛保温原油管段蜡沉积速率进行预测研究，得出：

（1）根据实验室内进行的54 组实验，得到了油壁温差、流量和油温对蜡沉积速率的影响，采用极差分析法和方差分析法判断了影响庆吉混油蜡沉积速率因素的主次顺序为：油温> 油壁温差>流量。

（2）利用室内实验54 组中的36 组数据设为学习组，18 组设为验证组，通过SPSS 软件得到了逐步回归模型，通过MATLAB 软件得到，支持向量机模型。对比发现，逐步回归模型无论从精度还是稳定性上都不如支持向量机模型。

（3）利用得到的两种模型对现场蜡沉积速率进行预测，逐步回归模型的预测值要高于支持向量机模型预测值。冬季蜡沉积速率最大，夏季最小。逐步回归法可以很好地预测管段各处蜡沉积速率变化，支持向量机法预测值较为稳定。由此可见，室内模拟现场管道的蜡沉积实验仍存在很多弊端，不能很好地模拟实际工况下的湍流状态，应加强对现场情况参数的提取调查，除了一些基本数据，增加一些管道材料参数，例如粗糙度等来进行综合研究。