基于试验模态分析橡胶减振件的参数识别*
曹云丽,臧传相,余毅权
(南京中车浦镇海泰制动设备有限公司,江苏 南京 210000)
0 引 言
为实现结构模态分析中橡胶减振件的动力学特性的参数确认,笔者提出基于试验模态分析法[ 1-3](EMA)进行橡胶件参数识别。试验模态分析是通过对结构进行人为激励,并通过对输入及输出信号进行处理分析、特征抽取,实现参数识别,是一种动力学结构的逆问题。随着傅里叶变换的推广与计算机技术的发展,试验模态分析技术实现了飞速的发展。常见的基于频域法的阻尼参数识别方法有半功率带宽法、频率细化法、峰值法、导纳圆法等,基于时域法的阻尼参数识别方法有对数衰减率法、ITD法、STD法、随机减量法等[4-6]。此外,和法家,卢曦杨,佩白等[7-8]通过直接测试法试验研究了振动频率、激励振幅、预载荷与橡胶减震器动刚度的主要关系。
笔者以某轨道交通车辆用压缩机吊挂橡胶减振器为研究对象,从动力学参数物理意义与计算原理两方面论证了不同测试方法参数等效转换的可行性,并通过试验验证参数等效转换的准确性。
1 工作原理
通过单自由度振动系统自由振动方程推导出减振系统的模态阻尼参数(试验模态分析法),并通过与效粘滞阻尼参数(直接测试法)进行对比分析,建立两种参数理论解析关系,具体如下。
1.1 动刚度参数
单自由度粘性阻尼系统主要由弹簧、阻尼器及质点组成。单自由度动力学模型如图1所示。
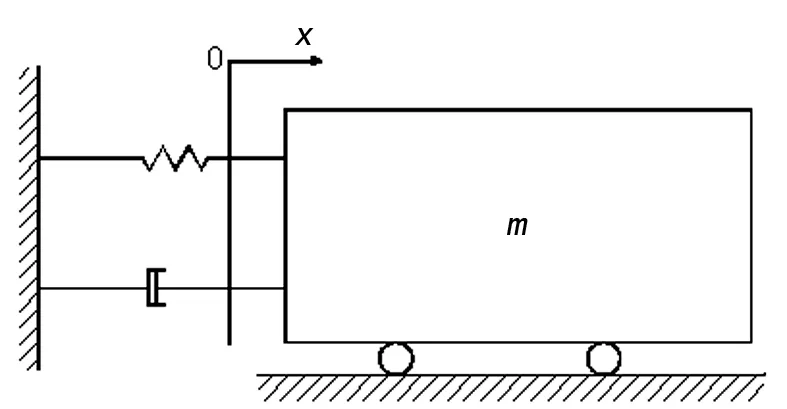
图1 单自由度动力学模型
单自由粘性阻尼系统,其自由振动动力学方程如下:
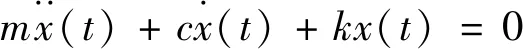
(1)
式中:m为系统质量;c为系统粘性阻尼;k为系统刚度;x为质点运动位移。
对动力学方程进行解析可知,系统的结构阻尼比为:
(2)

1.2 模态阻尼参数
(1) 基于时域的对数衰减法
假设系统自由振动响应为:
x(t)=Ae-ζωntsin(ωdt)
(3)

系统在某阶固有频率振动下,其结构阻尼比(即模态阻尼比)为:
(4)
式中:Ai、Ai+1为系统自由振动的第i、i+1个峰值。
(2) 基于频域信号的半功率法
单自由度系统的振动响应在频域内的表达式如下:
H(ω)=|H(ω)|ejθω
(5)
其中:
(6)
根据半功率法可得:
(7)
解方程(7)可知:
ω1=(1-ζ)ωn,ω2=(1+ζ)ωn
最终解得系统模态阻尼比如下:
(8)
1.3 等效粘滞阻尼参数
根据等效粘滞阻尼的力学模型,单自由系统振动周期内,从能量耗散角度计算系统等效粘滞阻尼,其表达式为:
Wd=πceqA2θ
(9)
式中:wd为系统周期振动过程中所耗散的能量;ceq为系统结构等效阻尼系数。根据系统等效阻尼系数的物理意义,振动系统周期耗散能量即为振动系统应力-应变滞回曲线所围成面积,如图2所示。

图2 结构应力-应变滞回曲线
故结构阻尼比可通过如下计算:
(10)
式中:ceq为系统等效粘滞阻尼;w为系统振动频率。
在振动系统在某固有振动频率下,减振件的结构等效阻尼参数可通过试验模态阻尼参数反向求得。
2 试验模态分析法测试
2.1 试验装置
为实现橡胶减振件模态参数快速识别,又不失一般性,根据基本原理建立自由度较少的弹簧-阻尼-质量的试验方案,弹簧及阻尼器由橡胶减振件承担,橡胶减振件选用某成熟工业产品。
试验设备采用法国OROS 32通道动态信号采集仪、美国PCB模态调谐力锤以及PCB三向加速度传感器,模态参数识别采用南京航空航天大学自主开发的N-modal模态分析软件。具体试验装置如图3所示。

图3 弹簧-阻尼-质量系统试验装置
2.2 试验方案
实验分别对43.80 kg、62.50 kg、81.45 kg、100.40 kg、125.25 kg的质量块进行了实验。由于质量块的结构较为简单,在铁块上表面均匀分布4个测点(处于表面四个顶点位置),测试位置如图4所示。

图4 试验测点分布
根据实测尺寸在 N-Modal模态分析软件中建立一个 4节点的几何模型。质量块结构模态主要的振动方向主要体现在垂直方向,在其他方向基本没有振动特征,因此测试主要针对结构垂直进行实验,每个测点测试一个方向,共计4个测试自由度。
2.3 激励信号
此次实验质量-弹簧系统是最简单的表现形式,采用的激励方式为锤击法,产生的激励信号为脉冲信号,在基础的模态实验中运用比较广泛且实用。
脉冲信号是一种离散信号,形状多种多样,与普通模拟信号(如正弦波)相比,波形之间在时间轴不连续(波形与波形之间有明显的间隔)但具有一定的周期性是它的特点。激励信号图如图5所示。
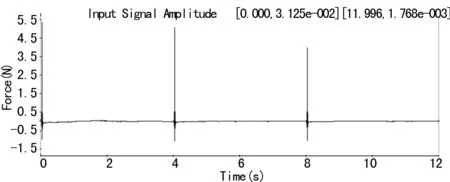
图5 力锤激励信号
2.4 互易性检验
对应线弹性系统,加速度响应满足互易性,因此加速度的频响函数也具有互易性,即i点单位激励产生j点响应与j点单位激励产生i点的响应相同,可表示为:
Hij(jω)=Hji(jω)
实验过程中,取两个个激励点处作为互易性的校验位置,得到的两点间互为激励和响应的频响函数曲线如图6所示。

图6 两个激励点间的互易性校核
从图中可以比较清楚的看出,实验较好的满足了线性条件,两条频响函数几乎重合,激励设备的安装较好的满足条件。
3 模态识别结果对比
主要针对刚度-阻尼-质量系统垂向刚度及垂向振动阻尼系数进行分析,未对系统转动、摆动动力学特性进行研究。由于刚体模态处于低频段,故仅对100 Hz以内的模态频率进行识别分析。质量块的质量为81.45 kg时,系统垂向模态振型及频响函数如图7、8所示。针对不同重量的质量块测试系统采用同样方法进行试验,不同质量块状态下模态参数识别结果如表1所列。

图7 垂向振动模态振型
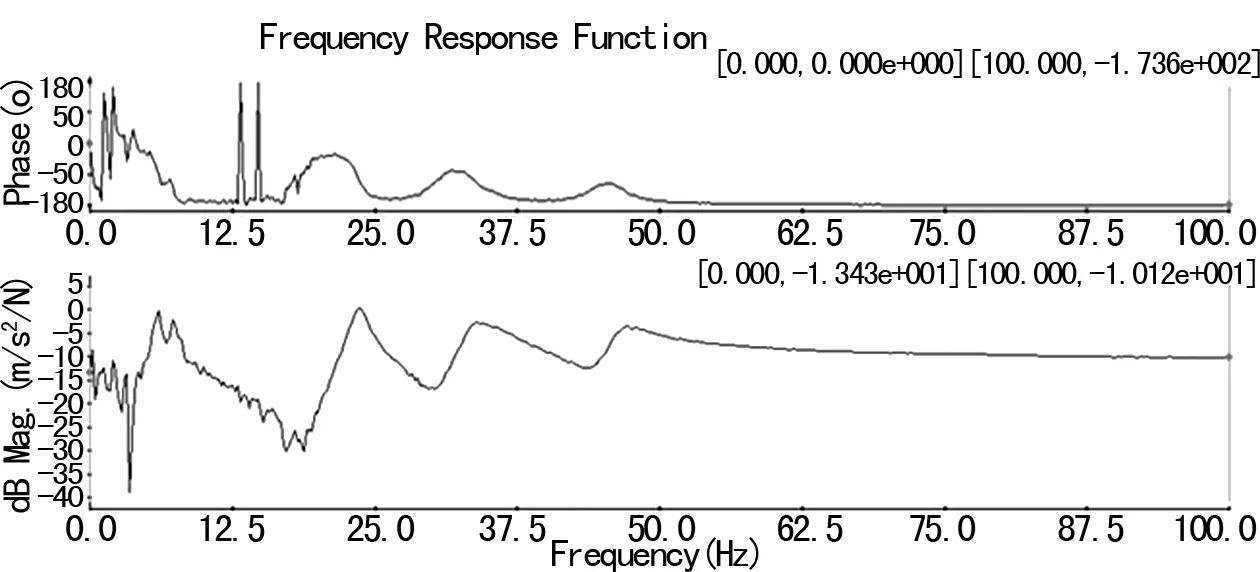
图8 垂向振动频响曲线

表1 模态参数识别
根据实验及计算出的数据,得到动刚度-频率关系拟合曲线与阻尼比-频率关系拟合曲线,如图9、10所示。

图9 动刚度-频率关系曲线
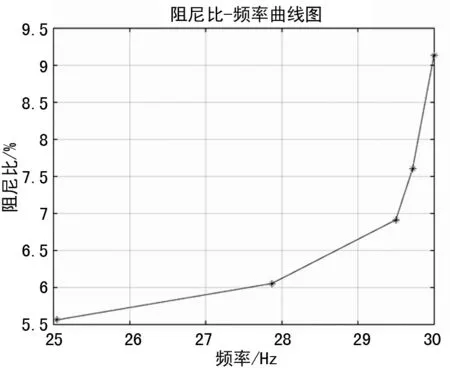
图10 模态阻尼比-频率关系曲线
通过对动刚度-频率和阻尼比-频率关系拟合曲线,可知在一定范围内,质量-弹簧系统中弹簧的刚度随着激励频率的增大而非线性减小,阻尼比随着频率的增大而非线性增大。
4 直接测试法测试
4.1 试验装置
为对比分析不同测试方法所测得的产品性能,现采用西安力创材料检测技术有限公司生产的PL-100电伺液服疲劳试验机进行减振件静刚度、动刚度测试,试验测试精度为1%,测试力值范围0~100 kN。测试样件、测试设备及测试安装示意图如图11所示。

图11 减振器测试样品及测试安装示意图
4.2 试验结果
文中测试方法采用TB/2843《机车车辆用橡胶弹性元件通用技术条件》中规定方法进行测试。静刚度测试:试验应在23 ℃±2 ℃恒温、环境湿度为50±10%的室内进行对试样进行加载,加载速率为3 mm/min,从零开始加载到试验载荷上限3 kN,然后快速卸载至零,连续重复上述试验过程三次,第三次试验时正式记录载荷-变形位移曲数据。动刚度测试:振幅均值0.22 mm,幅值0.11 mm,频率6 Hz。动作次数700次,取最后20次计算动刚度值。
通过对样品进行性能测试,测得数据如表2所列。
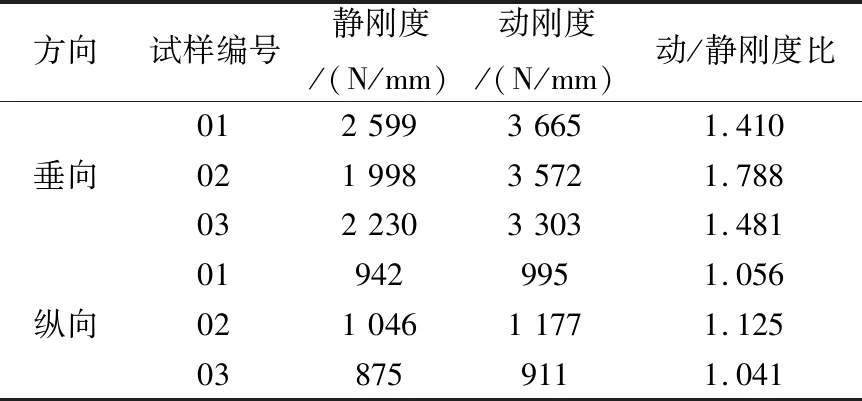
表2 减振件刚度试验测试结果
由于减振件为回转体,纵向与横向刚度与阻尼值相同,故本文中仅对纵向进行测试。通过分析可知,纵向刚度仅为约为垂向刚度的1/3,垂向动/静刚度比约为1.56,纵向动/静刚度比约为1.07。
5 分析与结论
通过研究分析可得出以下结论:
(1) 在某共振频率下,振动系统中模态阻尼与系统等效粘滞阻尼可实现换算。通过频域信号的阻尼比参数识别可反向计算出系统等效粘滞阻尼,从而与减振件的产品参数实现关联,通过此方法可实现高频振动条件下减振件动力学参数测试。
(2) 通过模态测试法进行橡胶减振件性能参数识别所得结果与直接测试所得结果略有差异,模态测试法识别出的25 Hz低频振动动刚度为3 112 N/mm,直接测试6 Hz振动频率下的动刚度平均值约为3 513 N/mm,两者数据相近,可认为模态测试法具有参考价值。
(3) 基于试验的模态分析技术可有效实现橡胶减振件刚度、阻尼参数的识别。产品动刚度随着频率的增大而非线性减小,模态阻尼随着频率的增加而非线性增加。上海理工大学的和法家[7]就针对动刚度与振动频率的关系做过研究,其研究表明相同振幅下,动刚度随频率变化趋势呈现先增大后减小的规律,从这个层面或许可以解释本文中产品在较高频率范围内呈现下降趋势,但此次针对这一趋势的研究与论证不够严谨,还有待进一步研究。

