利用matlab软件分析一个物理情景

陈建伟

(浙江省诸暨中学，浙江 诸暨 311800)

在某复习资料中曾经出现如下这个习题.

例题.电磁弹射是我国最新研究的重大科技项目，原理可用下述模型说明.如图1(甲)所示，虚线MN右侧存在一个竖直向上的匀强磁场，一边长L的正方形单匝金属线框abcd放在光滑水平面上，电阻为R，质量为m，ab边在磁场外侧紧靠MN虚线界.t=0时起磁感应强度B随时间t的变化规律是B=(B0+kt)，k为大于零的常数，空气阻力忽略不计.

图1

(1) 求t=0时刻，线框中的感应电流I及其功率P.

(2) 若线框cd边穿出磁场时速度为v，求线框穿出磁场过程中，安培力对线框所做的功W及通过导线截面的电荷量q.

(3) 若用相同的金属线绕制相同大小的n匝线框,如图1(乙)所示,在线框上加一质量为M的负载物，求t=0 时线框加速度的大小和方向.

笔者认为(2)问中“若线框cd边穿出磁场时速度为v”存在科学性问题.线框在既定的物理条件下从静止出发，是不可能冲出磁场的，分析如下.

设任意t时刻，cd边产生的位移为r，有

(1)

ma=BIL.

(2)

(3)

Φ=B(L-r)L.

(4)

B=(B0+kt).

(5)

解得

(6)

首先给题中各物理量随意数值化，即任意给定一个初始条件，不妨设置如下参数：L=1 m，m=3 kg，R=2 Ω，B0=2 T,k=0.5 T/s.

在matlab软件中输入上述二阶变系数微分方程，得出各物理量随时间的变化关系如图2-6所示.

图2 v0=0时r-t关系

图3 v0=0时v-t关系

图4 v0=0的对比图

图5 v0=0时F-t关系

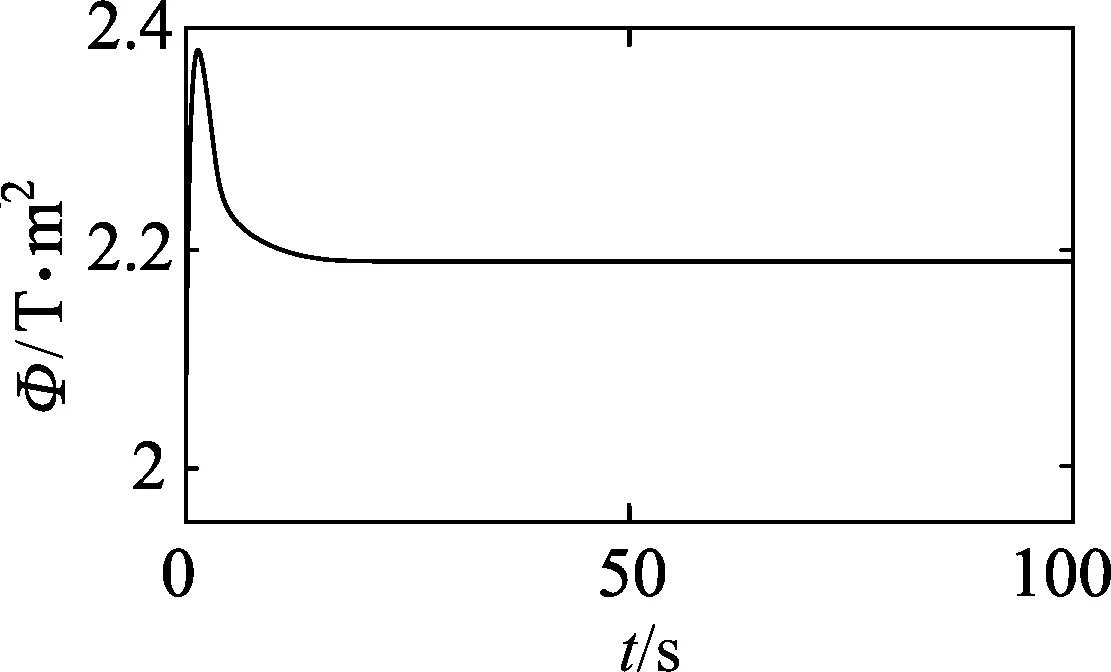
图6 v0=0时Φ-t关系

图2为位移r随时间t的变化图像，图3为速度v随时间t的变化图像，图4是把两个图像在同一图像中显示，图4的小图为20 s内明显变化时段的放大图.(左纵坐标为位移、右纵坐标为速度)，从图中不难发现位移趋向于1 m时，速度趋向于0.

图5是安培力F随时间而变化关系，可以发现足够长时间后力趋向于0，图6是磁通量Φ随时间而变化关系，足够长时间后磁通量趋向于定值.

分析如下.

t=0开始，磁通量Φ增大，安培力F向左，cd向左运动，速度增大.但是可以发现t=0时刻，F最大，此后F慢慢减小.可以推断，开始运动后，在公式中F=BIL中，尽管磁感应强度B在增大，但是k不变，回路面积减小，感生电动势减小，又cd棒向左运动，产生了与感生电动势方向相反的动生电动势，因此总电动势减小，总电流I减小，最终由图像可见F减小.

从图中可以看到，当位移大致为r=0.16 m时，磁通量Φ达到最大值，此后开始减小.可以推断这是由于cd向左的较大速度引起的磁通量减小程度大于由磁感应强度增大所引起的磁通量增大程度而产生的结果(初始Φ=2 Wb，最大时约Φ=2.4 Wb).因此安培力F反向向右(且可以看到此后向右的力先增大后减小最终趋向于0)，相应的速度开始减小(最大速度约v=0.145 m/s).

长时间后磁通量趋向于某一定值(约2.18 Wb)，速度、安培力趋向于0，r趋向于1 m，可以推断出最终cd会停在磁场内侧无限接近于边界处.(磁通量为某一定值是无限大磁感应强大与无限小面积乘积的结果)

由此可得，在上述既定数值的物理条件下，cd边不可能穿出磁场.

为了使结果有普适性，接着笔者更改了上述所有物理量的初始条件(唯有初速度为0保持不变)，经过运行后得到的结果，依然是cd边不可能穿出磁场.(运行过程相似，只不过是速度开始减小的时刻和位移值、各种最大值等改变了)

综上分析，笔者认为本题情景，线框从静止出发，是不可能穿出磁场的.

那么在初速度不为0的情况下，结果又会如何呢？笔者依然保持如上一样的物理量初始条件.并且给予一定的初速度，经过多次运行发现，当初速度比较小的情况下，cd依然不能穿出磁场，如图7中v=0.1 m/s的情况，如图8中v=0.25 m/s的情况.

图7

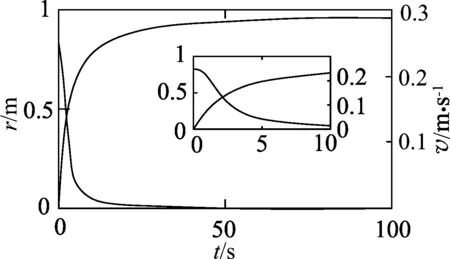
图8

当初速度比较大的情况下，cd可以穿出磁场，如图9中v=0.85 m/s的情况，如图10中v=1.2 m/s的情况.

图9

图10

从上述4种情况，可知当v=0.1 m/s的情况，速度是先增加后减小，另外3种情况速度直接开始减小.可以根据如下的计算得出v=0.25 m/s是直接开始减速的最小初速度.

由(6)式， 要求当t=0，r=0时，

(7)

解得

(8)

即当初速度为0.25 m/s时，一出发cd就开始减速了，从图中也可以看出.

经过多次调试，当初速度大约为v=0.85 m/s，cd刚刚能出磁场，由图9可以看出.

为了结果的普适性，笔者继续更改了上述所有物理量的初始条件，经过运行后得到的结果，依然初速度较小的情况下，cd不能出磁场，当初速度较大的情况下，cd能出磁场，当然不同的初始条件下速度的临界值也就不一样了.

综上可知，当有一定初速度的情况下，初速度较小的情况下，cd不能出磁场，当初速度较大的情况下，cd能出磁场.