基于三维图解静力学的复杂冰雪结构的计算性设计与数控建造＊

王祥 张啸 贾永恒 王聪 余忠晟

1 同济大学建筑与城市规划学院

2 哈尔滨工业大学建筑学院

1 研究背景

图解静力学作为结构静力学理论中的重要工具和设计方法，在近几十年的大量结构创新性项目和研究中被广泛应用[1]。随着当代计算性设计方法的普及以及计算机算法辅助设计的大量应用，相关设计插件的出现也带来了当代众多以图解静力学为依据的基本结构类型的找形设计方法[2]。传统图解静力学以力的多边形法则为基础，通过将空间平衡力系理解成反映结构中力传递的“形”图解以及力系之间平衡所构成的“力”图解，一方面可以将结构平衡问题的求解转化为“力”图解中封闭多边形的构造问题，另一方面也可以将结构中三维平衡的内力快速地可视化呈现。同时，对于设计师而言，结构设计的基本问题也从抽象的平衡方程求解转化成更加直观地对结构内力的主动性控制过程。

然而，传统图解静力学囿于其形与力的二维对偶性质的基本理论依托，往往只能局限地应用于二维桁架、索结构、壳结构等拓扑关系为二维流线的“曲面化”结构找形设计中。2016年，瑞士苏黎世联邦理工学院（ETH）的马苏德·阿克巴扎德（Masoud Akbazardeh）在其博士研究中创新地根据麦克斯韦（Maxwell）和朗肯（Rankine）于19世纪提出的三维多面体力系的平衡与三维封闭多面体的对偶性质[3-4]，将二维图解静力学理论延伸到三维，提出了关于三维图解静力学的基本结构理论、几何理论以及与之相对应的一般性设计方法[5]。顾名思义，三维图解静力学拓展了传统图解静力学所涉及的形态的维度，将图解静力学的应用范围从只可被二维化抽象定义的平衡结构拓展到复杂的三维平衡结构。

本文基于三维图解静力学的基本理论，从两个案例探讨基于三维多面体对偶性质的图解静力学设计方法以及其应用可能，并从数字建造技术的角度展现其在冰雪建造为代表的材料性能化设计探索中的巨大应用潜力。

2 三维图解静力学的一般原理

2.1 二维图解静力学中的力多边形法则

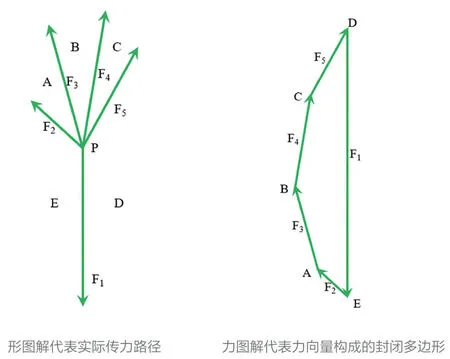
传统图解静力学理论中，二维平面平衡力系可以通过向量平移的方法转化为首尾相接的连续封闭的力多边形，因此也被称为“力的多边形法则”。

如图1左图所示，五个共面外力F1～F5构成平面平衡力系（五个力的合力为零），即为该平衡力系的“形”图解，其中五个外力由FN表示，外力交于一点P，并将平面空间分为顺时针A～E表示的五个子空间。根据力的向量表示法，该平衡力系的五个分量可以通过平移的方式进行首尾相接，从而构成一个围合封闭的连续多边形，如图1右图所示，亦称作该平衡力系的“力”图解。在“力”图解中，原有合力在平面内的共点P转化为一个闭合的力多边形，“力”多边形的顶点即代表“形”图解中被外力分隔形成的子空间，这种图形之间的对偶性质也被称为“形”图解和“力”图解间的“互逆”（Reciprocal）关系。

2.2 三维图解静力学中的多面体对偶性质

三维图解静力学考虑了空间平衡力系的更加一般的对偶性质。其中，三维平衡力系不再使用投影的方法将其转化为平面力系进行求解，而是根据麦克斯韦和朗肯提出的对偶理论，将其与三维封闭的力多面体相匹配，从而建立出更高维度下图解静力学中多面体之间的对偶关系。

如图2所示，四个空间外力在点P处达到平衡，在相应的“力”图解中，交点被表示成一个封闭的力四面体，“形”图解中的四个力被表示为力图解中的四个对应的面，面的方向垂直于“形”图解中“力”向量的方向，其面积等于“形”图解中平衡状态下力的大小。

1 二维图解静力学的基本原理——力的多边形法则

2 三维图解静力学基本原理——推力线形图解和空间多面体力图解间的对偶关系

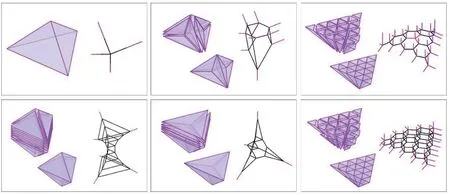
3 基于力多面体组构模式的图解静力学生形的基本原型分析

4 “实验椅”案例中初始力多面体组合方式研究和模式确立

5 “实验椅”案例中针对深化、优化设计的力多面体剖分研究

6 “实验椅”案例的结构有限元分析验证及最终建造效果

3 基于三维图解静力学的空间结构找形设计方法——以一个“实验椅”为例

三维图解静力学中抽象的形与力的关系使其往往很难直接用于结构创新性设计之中，本节针对此问题，结合一个教学课程作业——“实验椅”的设计过程，探讨基于三维图解静力学的基本设计方法。

3.1 力多面体的拆分模式与结构形态

与二维图解静力学不同，三维图解静力学的设计过程往往直接从三维“力”图解的架构开始，因此初始力多面体的构造方式往往决定了结构设计中的基本形态（图3展示了多种初始多面体及多面体组合对应的形图解的几何构造特征）。因此，应用三维图解静力学进行的空间结构找形，首先需要根据结构受力特征的假定，建立相关初始力多面体组合。在本案例的受力模型设计中，将椅腿四个支点作为固定支座，为简化模型将椅背也作为固定支座，施加荷载分解为竖直向下对椅面的压力和水平对椅背的侧推力，由此构造了简单的力多面体簇，初步建立了椅子的受力模型（图4）。

3.2 力多面体的细分与形态优化

初始力多面体的构造代表了初步设计中对于基本结构纯受压传力路径的基本假设，同时，在力图解中对一个力多面体按照某种规则剖分，在保证力多面体仍然封闭的情况下，分解的小多面体簇可以看成是平衡力系中全局力不变条件下对作用力分解的等效。因此，多面体细分的方法也是结构深化设计和优化设计中的重要方法。

在本例中，设计者从椅面开始，通过力多面体的剖分和增加新的多面体来改变结构受力的拓扑关系：首先将椅面看作四个支座点进行细分，形成平衡的平面力系；其次向下增加力多面体改变全局力，使其变为最终受力传向四个椅腿支座点的三维平衡力系；最后对其内部结构进行合适的剖分变成对偶图形理想的力多面体簇（图5）。

3.3 三维图解静力学找形与结构性能的匹配

在三维图解静力学中，结构的初始形态定义和最终的平衡确认过程被独立地分成了结构初始形图解或“力”图解的基本形态组构，以及“形”图解和“力”图解几何关系的二次优化（如“形”图解中的力向量和力图解中对应的平面垂直关系）的问题。因此，在形与力的操作过程中，设计者可以从任何一个图解的形态操作入手，对目标形态进行调整和限定，最后通过针对整体应用最优化方法，使“形”图解和“力”图解实现“垂直化”，以寻找最终平衡后的全局力系。

图解静力学原理在特定边界条件下的设计问题中，通过图解操作和拆分组合的方法给出了符合条件的最优传力的拓扑结构，适合于大量针对材料性能、加工性能等有特殊需求的结构设计问题。如在本案例中，材料的选择为0.5mm超薄钢板，其空腔式的结构形态使其表面受力性能远远弱于延折痕方向的结构性能。同时，平板式的原材料类型也使结构的加工适合于由平面构成的多面体腔体结构。因此，在结构早期的设计过程中对相关传力路径（图6为结构的有限元计算模型，展示了应力主要沿折痕形成的瓦楞区域分布）、结构的基本几何形式加以考虑，可以更加高效地使用材料和结构形式。

4 三维图解静力学启发下的复杂冰雪结构计算性设计与数控建造

冰是一种坚硬而易碎的材料，可以承受较大的压力，而抗拉、抗弯、抗剪等性能较差，因此冰雪结构最合理的设计方法就是通过对结构形态和建造方式的设计，尽量满足材料本身的结构性能要求。图解静力学的原则就是使力与形的关系相互匹配，与“力”图解相匹配的“形”图解受力只沿着杆件的轴向传递，因此每个杆件并不受弯矩，这种受力特点非常适合冰这种材料。

4.1 找形流程

7 冰雪结构的初步三维图解静力学找形

8 冰雪结构的深化设计与几何优化

9 冰雪结构的机器人辅助加工示意

10 冰雪构件的连接工艺试验

11 最终完成的机械臂辅助加工的三维图解静力学冰雪结构

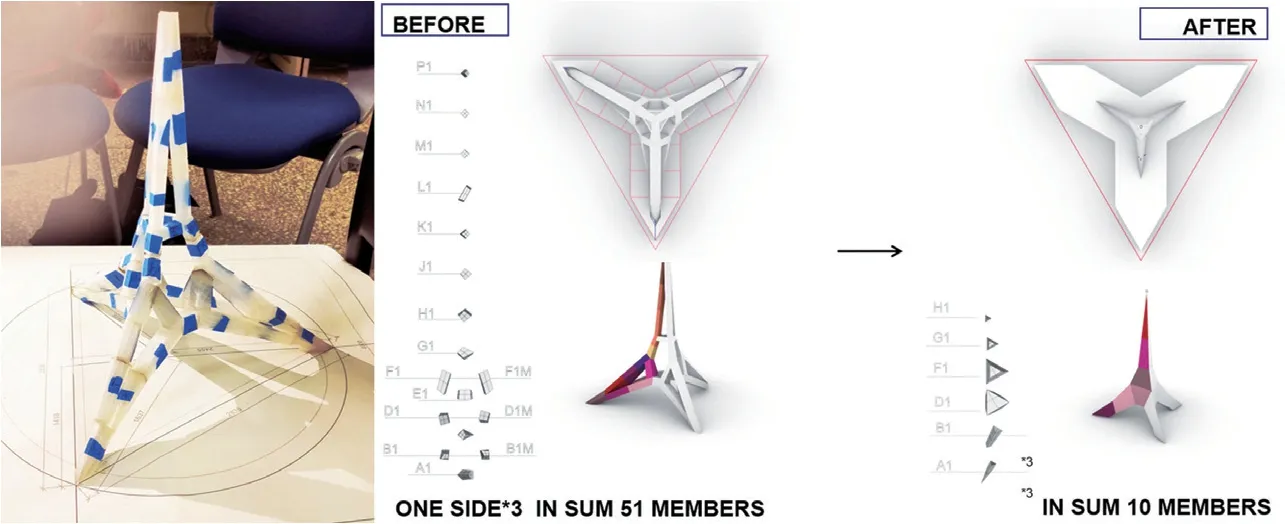
结构找形以基本的三维图解静力学的多面体剖分开始，以正四面体为原型，通过对某一三角平面向上的多面体进行细分，以增加最终结构核心部位的杆件数量。多面体细分基本分为两个层级：第一层级为对构筑物“核心”的细分，以正四面体中心为起点，向四个顶点连线，将正四面体均分为四组四面体；第二层级是对构筑物“枝干”的细分，将其细分为两组四面体组合，以形成枝干三棱锥的几何形态（图7）。同时考虑到加工时间等因素，研究最终选择的杆件数量为30根整，并以此为基础进行几何深化。

4.2 几何优化

为将找形获得的几何线框优化成可供数控加工并组装的冰块构件，需要进行几何深化工作。在此出现过两种深化方式的探讨：方案一是以每条杆件为路径进行单轨扫掠形成柱体；方案二是以每个杆件作为冰块多面体的轮廓，直接形成最终的冰块几何。研究中首先对方案一进行了1:10的模型搭建，即使是通过高精度的3D打印，每个冰块单元在拼接过程中仍出现了较大的累计误差，因此为减少加工冰块的数量并减少累计误差，最终决定采用方案二，即以多面体棱台的基础几何进行切割，并适当缩小构筑物的总体尺寸，以满足选用的机械臂建造方式对每个单元的加工半径需求（图8）。

4.3 机械臂加工及最终结构搭建

结构本身的多面体形态和最终优化的单元构件尺寸，使最终的结构建造可以通过机器人辅助的带锯切割以全过程数字化控制的方式来完成。基于研究团队自主开发的FURobot机器人控制插件[6]，本研究对KUKA机械臂定制了相应刀路，机械臂工具端沿着此路径运动，使线锯的切割路径形成一个直纹曲面（本例中多为平面），完成对冰块的切割（图9）。

在现场搭建过程中，团队以450 mm 高、700mm×1 650mm的三条冰台为基础，在其上进行整体基础定位，并使用泡沫板作为整体核心结构的临时支撑。然后，团队将整个构筑物的三条落地构件先完成粘贴。此工作需要首先将两个连接的冰块表面打磨平滑，再使用热水均匀少量地涂抹在冰块表面，再快速将两个几何体对准粘牢，此后使用少量冰雪混合物加固粘贴的缝隙，最终使水冻结（图10）。在完成冰块的粘贴安装后，将临时泡沫塑料支撑撤除，完成最终构筑物的整体搭建（图11）。

5 结论与展望

综上所述，图解静力学通过对结构传力路径和结构拓扑关系的合理设计和找形，实现了针对材料基本性能和加工工艺双方面优化的性能化设计方法。针对冰雪结构的建造，在传统结构认知的基础之上，整合了更加前沿的数字化设计方法和机器人辅助的高精度加工方式，再结合三维图解静力学的应用，能够为未来新材料驱动下的结构性能化设计提供更加多元、新颖的发展方向。同时，结合相关工艺生成一体化的建造策略以及整合性的设计工具，也是未来计算性设计与结构性能化设计发展的重要方向。

致谢：本研究作为2019 中国建筑学会计算性设计学术委员会第一届数字设计及建造工作坊的研究成果，作者对中国建筑学会计算性设计学术委员会以及学会活动组织者致以衷心的感谢。同时，作者也对全体小组成员仲美玲、国珂宁、邱明楚、何昕宇、吴凌菊、于鑫宇、田凯宁、谢莹粲、宋宣齐、朱映恺、周栩至、赵田、杨岳等的辛苦工作表示感谢。

图片来源

所有图片均为作者自绘或自摄。