改进弦长抽样方法开发及在弥散燃料蒙特卡罗模拟的应用

刘仕倡，王 侃，陈义学

(1.华北电力大学 核科学与工程学院，北京 102206；2.清华大学 工程物理系，北京 102206)

弥散型燃料是将核燃料弥散地分布在非裂变材料(金属、石墨)中。由于其具有燃料温度高、燃耗深度深、裂变产物包容性好等特点，广泛应用于高温气冷堆、钍基熔盐堆、事故容忍燃料、实验研究堆及核动力舰船。针对弥散型燃料的随机非均匀特性，国内外研究提出了3类方法：重复结构随机栅格方法、弦长抽样(CLS)方法和显式模拟方法。其中显式模拟方法对燃料颗粒进行随机堆叠，是采用近似最少的方法。然而，颗粒堆叠最常用的随机序列添加法的体积填充率上限为38%[1]，无法满足一些高体积填充率的设计，如全陶瓷微胶囊封装(FCM)燃料的需求。其他堆叠方法如离散元法步骤复杂且耗时较多。CLS方法无需显式地描述所有随机介质，而是在中子输运过程中对随机介质的距离(即弦长)和角度进行抽样。CLS方法的最大优势在于它能简化几何建模，提高计算效率。自20世纪90年代直至近年来，Zimmerman等[2]、Ji等[3]、Liang等[4]对CLS方法开展了大量研究，MVP[5]和Serpent[6]等程序亦采用了该方法。自主化堆用蒙特卡罗程序RMC[7]中也开发了显式模拟法和CLS方法的相应功能，并对比了不同方法间精度和效率的差别[8-9]。然而，传统CLS方法在高体积填充率时误差较大。另外，传统CLS方法只能描述单种颗粒的填充，无法对多种颗粒(如燃料颗粒和毒物颗粒)混合填充的情况进行模型。本文针对CLS方法的两大问题，在RMC中开发改进CLS方法，并采用含弥散燃料的燃料棒算例及含毒物颗粒的高温堆燃料球算例进行验证。

1 多种类型颗粒的CLS方法

CLS方法的核心思想是使用概率分布函数描述随机介质中颗粒表面的位置。中子到颗粒表面的距离通过抽样产生而非显式地对所有颗粒进行建模，在填充随机几何的区域内只存在1个颗粒，该颗粒的位置不固定，而是在中子输运过程中动态确定，从而可有效减少完全显式建模的时间消耗。

CLS方法的抽样过程如图1所示，分为两步。

图1 CLS方法示意图Fig.1 Schematic diagram of CLS method

第1步确定下一个颗粒表面的入射点A，令中子在离开当前颗粒后，到下一个颗粒表面的距离为λ1，λ1称为基体的弦长。推导可得基体的平均弦长为式(1)，r为颗粒半径，PF为颗粒的体积填充率。λ1分布可近似为指数分布，可得弦长概率分布函数如式(2)所示。通过式(2)抽样出λ1，即可确定入射点A。

(1)

(2)

第2步确定下一个颗粒的球心位置(x,y,z)。中子进入颗粒的夹角θ可通过其余弦值μ=cosθ抽样得到，如式(3)所示，ξ为(0,1)之间的随机数。

(3)

得到夹角θ后，根据A点坐标及颗粒半径r，可得到球心位置(x,y,z)。

CLS方法的优势在于可达到很高的体积填充率，然而传统蒙特卡罗程序(如Serpent)中的CLS方法仅能对1种类型的颗粒进行抽样，无法处理同时填充多种类型颗粒的问题，大幅限制了CLS方法的适用范围。

本文通过理论推导，提出了多种颗粒类型的CLS方法，并在RMC中进行实现。

假设存在两种类型的颗粒，半径分别是r1和r2，则颗粒的弦长分别是4r1/3和4r2/3，填充率为PF1和PF2。假设两种颗粒抽样出现的次数为N1和N2，则抽样次数与填充率的关系为：

(4)

可得：

(5)

根据N1/N2即可得到在弦长抽样过程中不同类型颗粒抽样出现的概率，其概率分别为N1/(N1+N2)和N2/(N1+N2)。还需求出平均弦长L，根据颗粒的总体积填充率PF1+PF2，可得：

(6)

则：

(7)

如果r1=r2，则式(7)退回到式(1)，进而，可推广到N种颗粒的情况下，平均弦长为：

(8)

第i种颗粒的抽样概率为：

(9)

在多种颗粒类型的CLS方法中，与图1不同有两处，首先是抽样λ1所用的平均弦长由式(1)改成式(7)，然后根据式(9)抽样中子进入的颗粒的类型，如图2所示，再根据λ1和该类型颗粒的半径，确定颗粒的球心位置。

图2 多种类型颗粒的CLS方法示意图Fig.2 Schematic diagram of CLS method with polytype particles

2 体积填充率修正方法

传统CLS方法在高体积填充率时误差较大，这是由于CLS方法本身的理论假设未考虑颗粒间不能重叠的因素，从而在填充率较高时会产生方法本身的理论误差。本文提出一种体积填充率的修正方法，保证体积填充率的准确性。步骤如下：

1) 将所有材料设为真空，中子在真空中输运，不抽样碰撞距离，因此只能进行穿面，通过设定最大的穿面数，达到后中子死去；

2) 设置输入的目标体积填充率为PF1，进行通量统计，从而得到不同栅格的径迹长度，即得实际体积填充率PF2；

3) 根据PF1和PF2，可得到新的输入体积填充率PF3=PF1PF1/PF2；

4) 将输入体积填充率设置为PF3，重复步骤2，直到输入体积填充率与蒙特卡罗统计的实际体积填充率的误差在允许范围内。

通过RMC的体积计算功能，可对CLS方法的输入体积填充率进行定量修正，从而解决了CLS方法在高体积填充率时输入填充率与目标填充率不一致的问题，提高了CLS方法的准确性。同时由于RMC的体积计算耗时较少，因此体积填充率修正的耗时与蒙特卡罗输运计算相比是很少的。

3 结果与分析

采用FCM燃料棒算例及含毒物颗粒的高温堆燃料球算例，进行中子输运及燃耗计算，对改进CLS方法进行验证。除了CLS方法，还采用了显示建模法作为参考解。需指出的是，CLS方法与燃耗计算结合时，相当于同种类型颗粒合并为1个燃耗区进行燃耗计算。

3.1 FCM燃料棒算例

第1个算例为FCM燃料六边形组件算例，该组件以VVER-1000组件为基础，将其中的UO2燃料棒替换为FCM燃料，即以碳化铀(UC)为燃料核心的TRISO颗粒，随机弥散在碳化硅基体中，包壳材料采用FeCrAl，气隙为氦气，其参数列于表1。组件共有160根燃料棒，每根燃料棒有170 417个燃料颗粒，如图3所示。

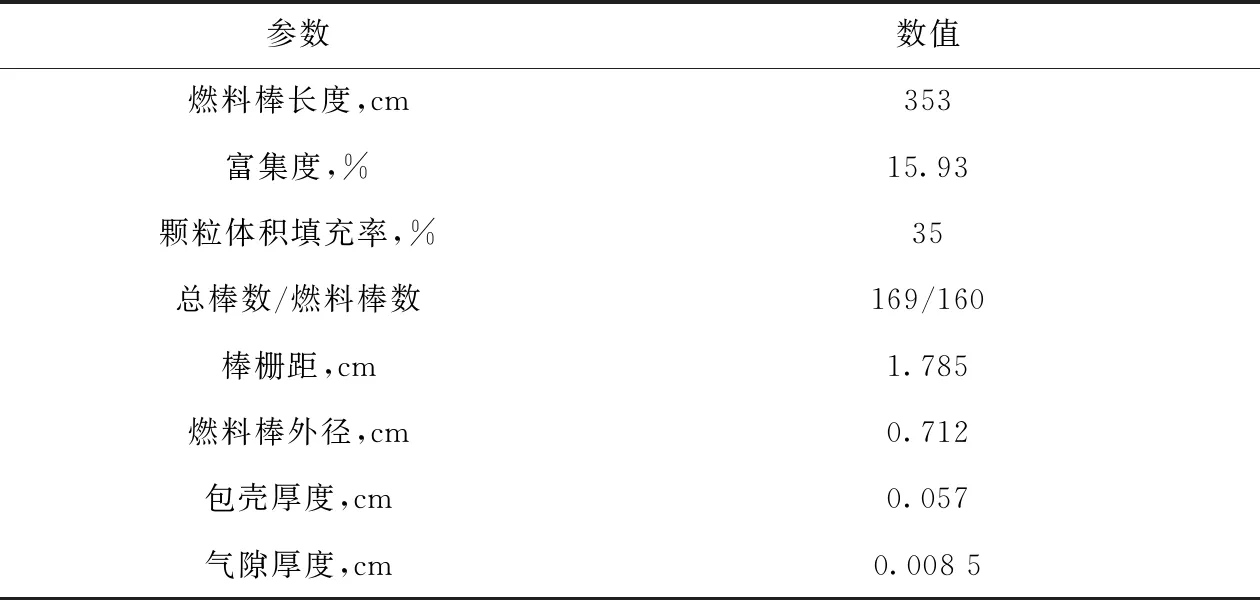
表1 FCM燃料六边形组件参数Table 1 Parameter of hexagon assembly for FCM fuel

图3 FCM燃料六边形组件Fig.3 Hexagon assembly of FCM fuel

在FCM燃料中，颗粒的实际填充率为35.000%。首先对输入体积填充率进行修改，如表2所列。当输入填充率达到35.000%时，实际填充率和输入填充率的相对误差达到9.065%。根据PF3=PF1PF1/PF2，利用RMC体积计算的功能，调整输入填充率为38.660%，从而达到目标填充率。

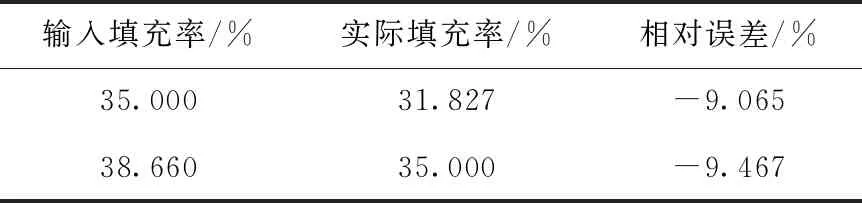
表2 CLS方法体积修正Table 2 Packing fraction correction of CLS method

然后分别采用显式建模法和CLS方法进行蒙特卡罗输运-燃耗计算。由于组件中总燃料颗粒数达到两千七百多万，显式建模法采用燃耗区合并策略，将每根燃料棒作为1个整体，将其中的170 417个燃料颗粒合并为同1个燃耗区，共160个燃耗区。同样，CLS方法也有160个燃耗区。采用3种情况进行对比：显式建模法、CLS方法(填充率35.000%，记为“CLS_35”)、CLS方法(填充率38.660%，记为“CLS_38”)。kinf对比如图4所示，图5为两种填充率的CLS方法与显式建模法对比的误差。计算条件为每代10 000个粒子，200个非活跃代，500个活跃代，kinf统计标准差为0.000 25。

图4 显式建模法和CLS方法kinf对比Fig.4 kinf comparison of CLS method and explicit modeling method

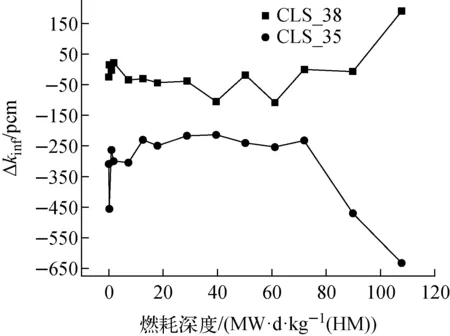
图5 两种填充率的CLS方法与显式建模法对比的误差Fig.5 Error between CLS method and explicit modeling method with two packing fractions

可看出，两种CLS方法与显式建模法的误差均较小，经过填充率修正后的CLS方法与显式建模法更接近，燃耗深度为107.806 MW·d/kg(HM)时，修正后的CLS方法的最大误差为190.8 pcm。

3.2 含毒物颗粒的高温堆燃料球算例

第2个算例采用含毒物颗粒的高温堆燃料球设计，燃料球外围是反射边界条件，参数列于表3，示意图如图6所示。

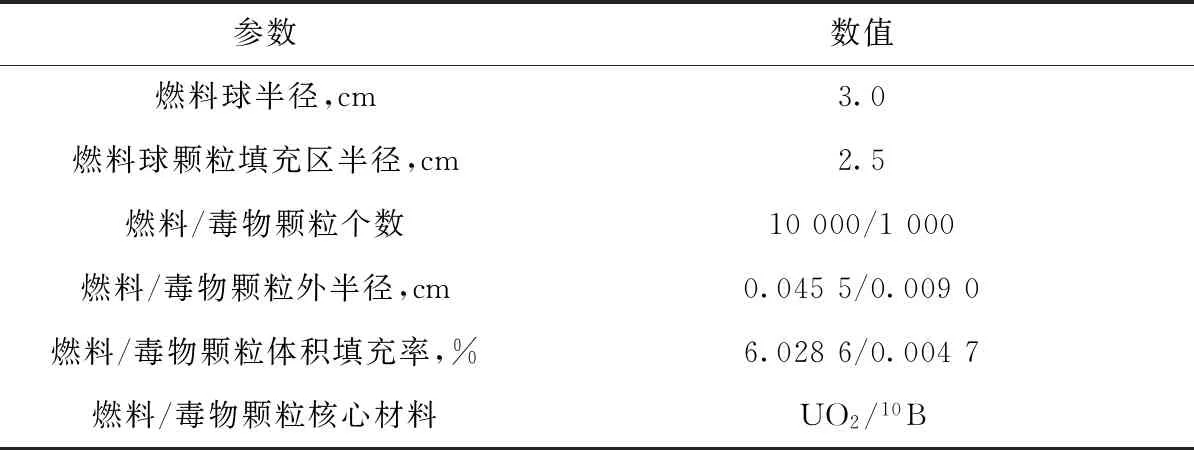
表3 含毒物燃料球参数Table 3 Parameter of fuel pebble with poison

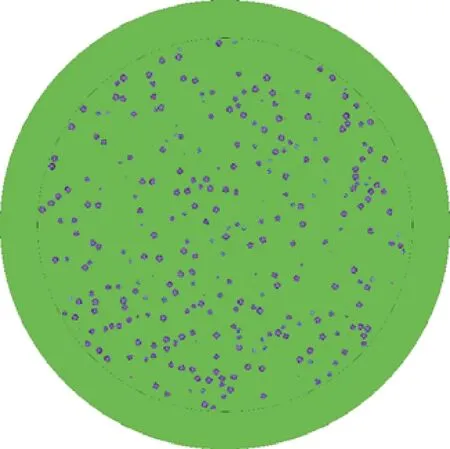
图6 含毒物的HTGR燃料球Fig.6 HTGR fuel pebble with poison

计算条件为每代10 000个粒子，50个非活跃代，550个活跃代，kinf统计标准差为0.000 32。采用4种方法对该算例进行计算，分别是显式建模法、显式建模法(合并燃耗区)、CLS方法、CLS方法(修正)，其中显式建模法有11 000个燃耗区，而其他3个方法均有两个燃耗区，分别对应燃料颗粒和毒物颗粒。CLS方法(修正)指根据实际体积填充率对输入体积填充率进行调整，分别是燃料颗粒填充率调整为6.117 9%，毒物颗粒填充率调整为0.004 8%。kinf对比如图7所示，以11 000个燃耗区的显式建模法为参考值，kinf差别如图8所示。可看出，显式建模法(合并燃耗区)的最大误差为99 pcm，而CLS方法修正后较修正前更接近参考值，修正后CLS方法的最大误差为169.7 pcm，未修正的CLS方法最大误差为308.5 pcm。

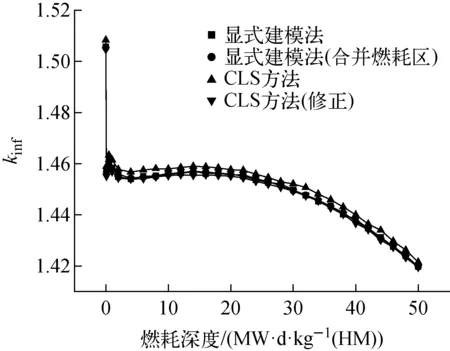
图7 含毒物HTGR燃料球的kinfFig.7 kinf of HTGR fuel pebble with poison

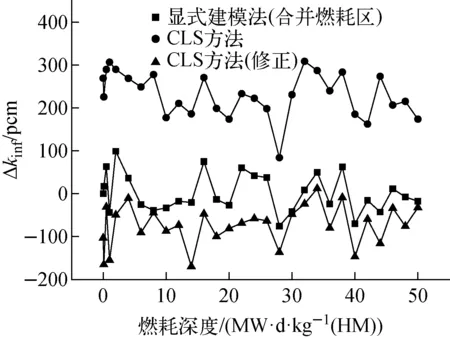
图8 含毒物HTGR燃料球的kinf对比Fig.8 kinf comparison of HTGR fuel pebble with poison

可见，显式建模法通过合理地合并燃耗区，可使误差在3倍统计标准差以内。另外，通过填充率修正后的CLS方法可提高计算的精度。

同时，表4比较了不同方法的耗时，可看出，合并燃耗区的显式建模法是不合并的显式建模法输运计算耗时的63.27%，燃耗计算耗时的0.31%；而CLS方法是不合并的显式建模法输运计算耗时的47.55%，燃耗计算耗时的0.31%。可见，合并燃耗区后，输运和燃耗计算耗时均大幅缩减。合并燃耗区时，CLS方法输运计算的效率较带网格加速的显式建模法的要高，耗时是其75.16%。

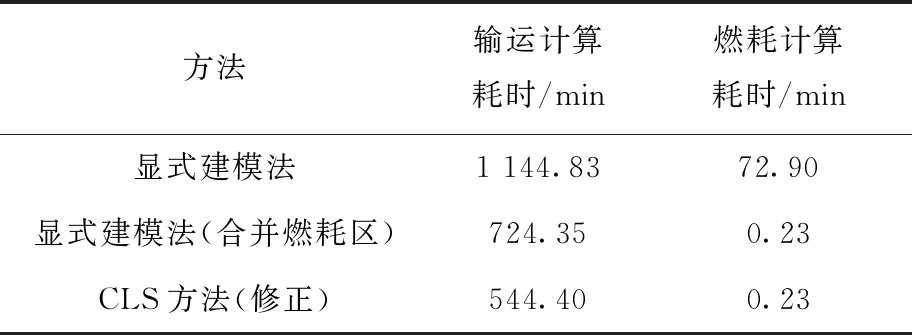
表4 含毒物燃料球算例计算时间对比Table 4 Calculation time comparison of fuel pebble with poison

4 结论

针对CLS方法的两大问题，本文在自主化堆用蒙特卡罗程序RMC中开发了改进CLS方法，包括多种类型颗粒处理及体积填充率修正方法。结果表明，该方法可解决多种颗粒混合填充的问题，并且可保证体积填充率的准确性，为弥散燃料的临界及燃耗计算提供了高效、精确的方法。