严重事故下气溶胶再悬浮的ECART模型分析

孙雪霆，季松涛，陈林林，史晓磊，魏严凇

(中国原子能科学研究院 反应堆工程技术研究部，北京 102413)

核电厂发生严重事故时，裂变产物以气溶胶形式沉积在固体表面。严重事故晚期，当在结构表面沉积的气溶胶所受的去除力大于使其附着在表面上的作用力时即可发生再悬浮。向重定位的堆芯熔融物注水造成的蒸汽爆炸、氢燃及氢爆等作用产生的气流会使沉积的气溶胶发生再悬浮。此外，事故造成的或有目的的回路卸压也会显著增加气流速率[1]。

气溶胶再悬浮的计算模型可分为两类[2-3]：1) 基于气动力或力矩与颗粒沉积表面的附着力或力矩之间平衡的准静态模型，包括力平衡模型、Reeks-Hall模型、Biasi模型、ECART模型等，其特点是当颗粒所受的气动力大于附着力时即会发生再悬浮，一旦超过颗粒悬浮的阈值，悬浮率由湍流爆的频率决定；2) 从能量积累角度分析的动态模型，颗粒振动获得足够能量脱离吸附势阱而离开表面，并由气流带走，包括RRH模型、VZFG模型和Rock’n’Roll模型等[2]，认为颗粒只有两点与表面接触，在空气动力学作用力波动影响下，颗粒在第2点附近振动，直到吸收足够旋转能量最终离开第1点。颗粒可在牵引力作用下滚动，也可在提升力足够时使自身升高，两种情况都会发生再悬浮。

ECART模型是根据颗粒受力来确定气溶胶再悬浮情况的准静态模型，当气动力超过附着力时就会导致再悬浮[4-5]。中国原子能科学研究院开发的严重事故下气溶胶行为分析程序CABSA的再悬浮模块中包括ECART模型，本文利用该模型对STORM项目的SR11试验[6]进行计算，分析气溶胶再悬浮的特性。

1 ECART模型

再悬浮基本发生在湍流流动中，且与湿度相关：周围气氛、沉积表面应为干燥。当气动力Faero超过使气溶胶附着在表面上的附着力Fadh时就会发生再悬浮，如图1所示[7]。以向上表面为例，沉积颗粒所受的气动力Faero包括由于湍流流动造成的拖曳力Fd和爆发力Fb，附着力Fadh包括使气溶胶维持在固体表面上的黏着力Fc和摩擦力Ff。当表面向上时，附着力中还包括重力Fg。这些力相互作用的结果是再悬浮的准则。ECART模型利用沉积在结构表面上的颗粒在各方向上的受力得出悬浮率，并通过试验数据推导得出半经验公式，悬浮率可对在各方向结构表面沉积的各种直径的气溶胶进行计算。

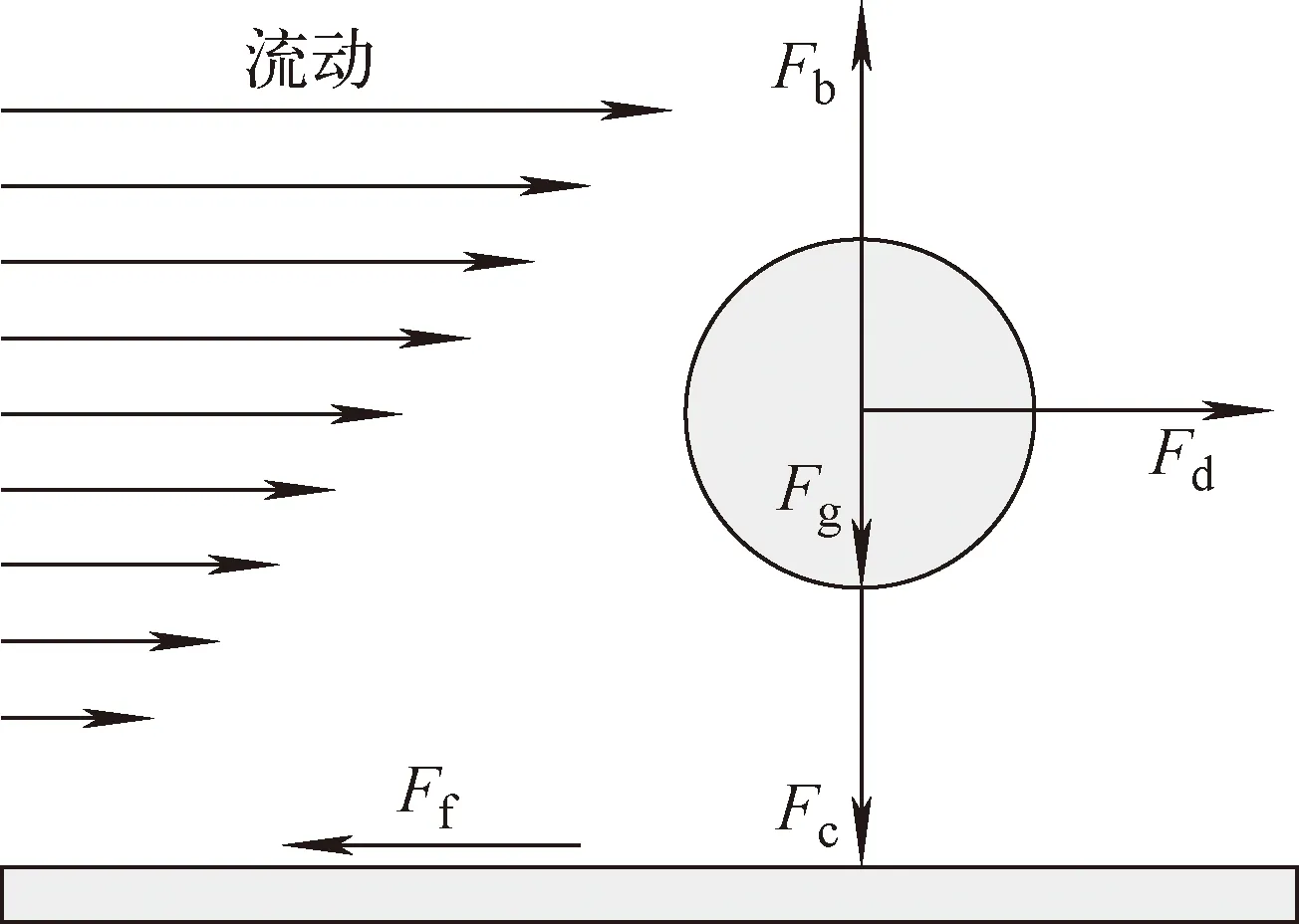
图1 气溶胶再悬浮受力Fig.1 Force of aerosol resuspension

1.1 再悬浮条件

当满足以下3个条件时，已沉积的气溶胶会发生再悬浮。

1) 湍流流动接近壁面，雷诺数Re满足Re≥2 300。

2) 系统干度。液相缺失，不存在水或其他液体。蒸汽饱和温度Tsat与温度裕度Tsr之和小于载流温度Tf与表面温度Tw二者最小值：

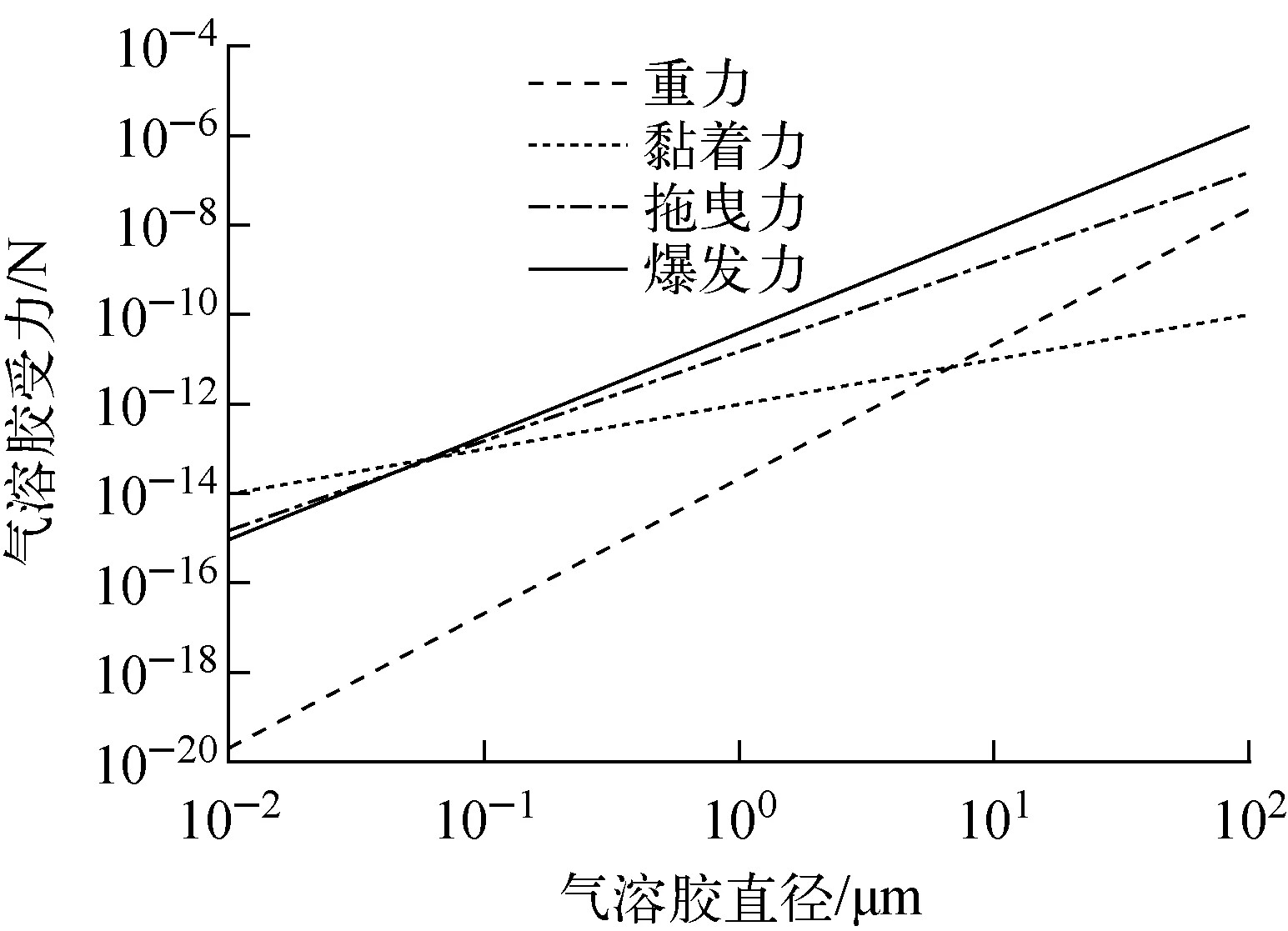
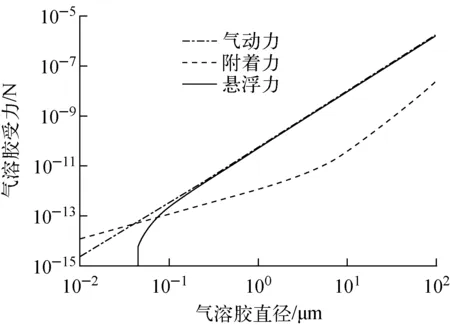
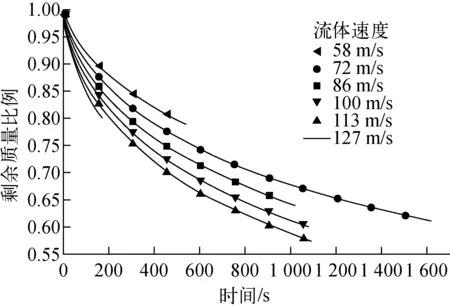
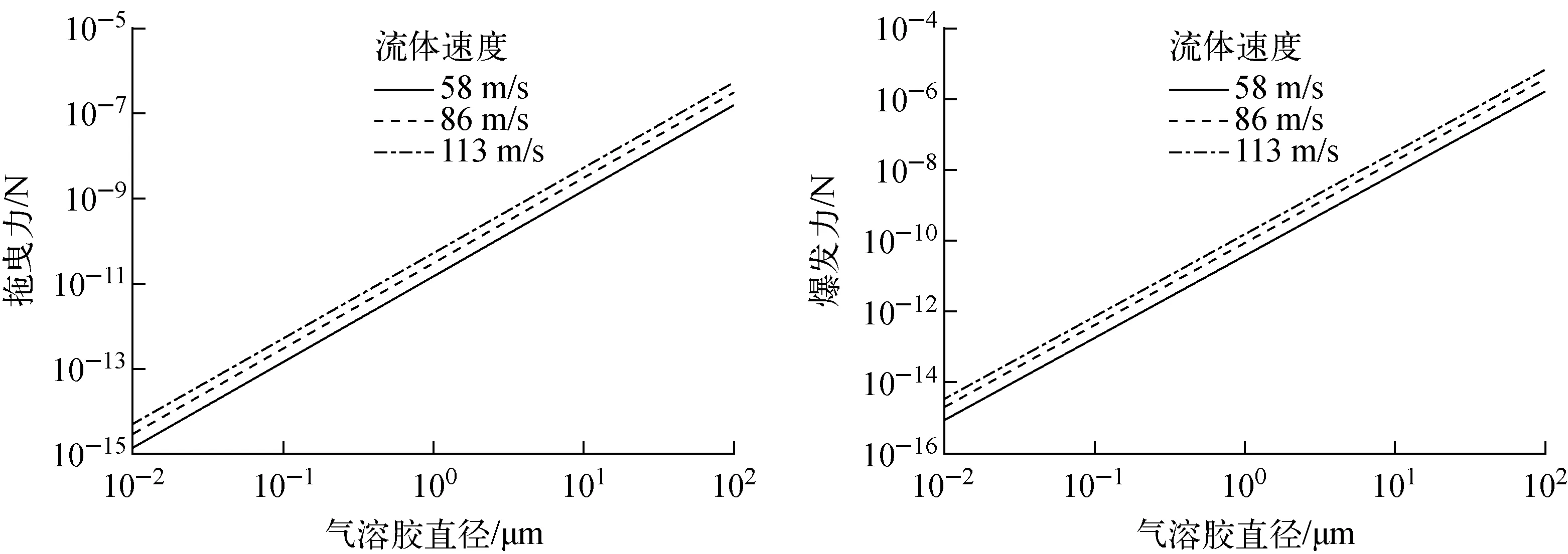
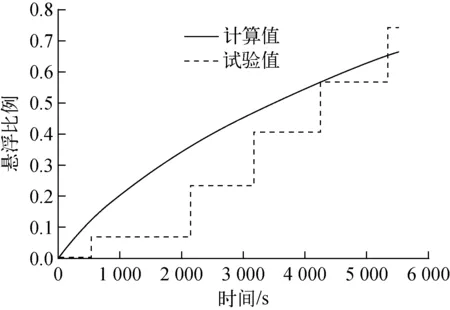
Tsat+Tsr

(1)

且min(Tf，Tw)小于沉积物质最低熔点温度TM，min与温度裕度Tsr之差，即：

min(Tf，Tw)

(2)

蒸汽饱和温度由下式得出：

(3)

其中：Tc为水的临界温度，647.3 K；pc为水的临界压力，22.064×106Pa；pH2O为蒸汽分压，Pa；Af为归一化系数，7.34[5]。

最低熔点温度TM，min定义为：当空间中无挥发性物质时，现有不挥发物质的最低熔点温度；当空间中有挥发性物质时，若挥发性物质凝结在气溶胶上并随之沉积，所有挥发性和非挥发性物质的最低熔点温度。

3) 悬浮力Fres。只有湍流流动造成的气动力Faero超过壁面上的附着力Fadh时才会发生再悬浮：

Fres=Faero-Fadh>0

(4)

1.2 与再悬浮相关的力

1) 使气溶胶保持沉积的附着力

ECART模型[5]中，附着力Fadh包括3种使气溶胶附着在固体表面的力，分别为重力Fg、黏着力Fc、摩擦力Ff。

重力Fg仅对水平向上表面有效：

(5)

其中：ρp为气溶胶密度，kg/m3；g为重力加速度，m/s2；d为气溶胶颗粒直径，m。

黏着力Fc为分子间相互吸引的作用力，包括静电力、范德华力等。

Fc=Hcγd

(6)

其中：Hc为取决于材料和系统属性的系数，对于两个光滑球体之间或完全光滑的球体与平面之间，0.000 8 N/m

摩擦力Ff是气溶胶在表面滚动或滑动时所受的阻力，来源于所有黏着力Fc。对于向上表面还包括重力Fg。对于竖直或向下表面：

Ff=fγFc

(7)

对于向上表面：

Ff=fγ(Fg+Fc)

(8)

其中，f为摩擦系数，0.2≤f≤0.55。

附着力Fadh为黏着力Fc和摩擦力Ff之和，对于向上表面还包含重力Fg。由式(5)～(7)可看出，附着力Fadh的3个分力均与结构表面流体速度无关。

2) 使气溶胶悬浮的气动力

气动力Faero能使气溶胶发生悬浮，分为与剪应力相关的拖曳力Fd和与湍流爆发相关的爆发力Fb。

假定沉积的气溶胶完全沉没在层流层中，且不会影响流速。流体作用在气溶胶上的拖曳力来源于经典流体力学：

(9)

剪应力τ0通过流体摩擦速度关系计算：

(10)

其中：u*为摩擦速度，m/s；χ为气溶胶动态形状因子，对于球形颗粒，动态形状因子为1；ρf为流体密度，kg/m3；u为流体速度，m/s；f为壁面范宁摩擦系数：

f=0.001 4 + 0.25Re-0.23

(11)

基于试验数据[8]，爆发力Fb为：

(12)

其中：Ab、Bb为常数，默认值取Ab=4.21±0.32，Bb=2.31±0.02[8]；ν为运动黏度。

气动力Faero为拖曳力Fd和爆发力Fb之和。由式(9)～(12)可看出，拖曳力Fd和爆发力Fb均与速度相关。

悬浮力Fres为气动力Faero和附着力Fadh之差，且对壁面及顶面和底面不同。对壁面及顶面：

Fres=Faero-Fadh=Fd+Fb-(Fc+fγFc)

(13)

对于底面，悬浮力Fres因受重力而更小：

Fres=Faero-Fadh=Fd+Fb-

(Fg+Fc+fγ(Fg+Fc))

(14)

1.3 气溶胶悬浮率

ECART模型是对Wurelingen、ART和STORM试验数据的经验修正而得出[9]。当悬浮力Fres>0时，有：

Λ(d)=e1(106Fres(d))e2

(15)

其中：Λ(d)为直径为d气溶胶的悬浮率，s-1；e1和e2为经验系数，当Fres<3.065×10-4μN时，e1=0.403 7，e2=0.600 3，当Fres≥3.065×10-4μN时，e1=90.28，e2=1.269[7]。

1.4 气溶胶悬浮质量

气溶胶悬浮的质量是对各时间步长的气溶胶悬浮质量求和，即：

(16)

其中：mres为气溶胶悬浮质量，kg；mdep为初始时刻沉积气溶胶质量，kg；Δt为时间步长，s。

2 计算分析

2.1 STORM试验

STORM试验的气溶胶再悬浮在长5 m、内径63 mm的试验段内进行，分为4个步骤[3]：1) 用氮气流将试验段温度提高至预定温度，以避免蒸汽凝结；2) 汽化室注入氮气/蒸汽混合气作为载流气体，并稳定一段时间；3) 利用等离子炬产生SnO2气溶胶，由氮气流带入试验段并在其中沉积；4) 当旁路再悬浮管中的氮气流温度压力稳定后，将气流切换到试验段开始再悬浮。其中步骤4分为多个阶段，各阶段氮气流的速度呈阶梯状提高。

2.2 计算模型

以试验SR11为例，用ECART模型计算再悬浮情况。悬浮开始时刻试验段内沉积颗粒质量为162 g，试验结束时试验段内沉积颗粒质量为42 g，试验各阶段的参数列于表1[3，10-11]。

表1 STORM SR11试验参数Table 1 Parameter of STORM SR11 test

计算控制体设为与试验段体积相等的长方体，流动截面设为与试验段截面面积相等的正方形，另外4个表面面积均为0.247 4 m2，表面温度为364 ℃。控制体内流体为纯N2，温度为370 ℃，压力为0.1 MPa。在壁面上沉积的小孔隙率SnO2气溶胶密度为4 000 kg/m3，质量浓度服从对数正态分布，几何平均直径μ=0.43 μm，几何标准差σ=1.7[3]。

2.3 计算结果与分析

1) 气溶胶受力

当流体速度u=58 m/s时，气溶胶所受各分力与气溶胶直径的关系如图2所示，可看出，重力Fg、黏着力Fc、拖曳力Fd、爆发力Fb均随气溶胶直径的增大而增大。由于气溶胶直径很小，与直径3次方呈正比的重力Fg在小直径范围相对于其他力要小2个数量级，但其随直径的增长要比其他力更快；拖曳力Fd和爆发力Fb随直径的增速比黏着力Fc更快。

图2 气溶胶受力Fig.2 Force on aerosol

图3示出气溶胶所受合力。由图3可见，气动力Faero和附着力Fadh均随直径的增大而增大，其中气动力Faero增大得更快。根据式(13)和(14)，气溶胶所受的悬浮力Fres也随直径的增大而增大。当d<0.049 8 μm时，附着力Fadh大于气动力Faero，在该范围内，悬浮力Fres<0，即该直径范围的气溶胶附着在结构表面未发生悬浮。故从气溶胶所受合力对气溶胶直径的关系可看出，直径大的气溶胶更容易发生悬浮。

图3 气溶胶所受合力Fig.3 Composite force on aerosol

2) 气溶胶悬浮率

气溶胶悬浮率与直径的关系如图4所示。对比图3可看出，悬浮率Λ和气溶胶受力的变化趋势相同。根据式(15)，悬浮率Λ与悬浮力Fres呈正比，故气溶胶直径越大，悬浮率Λ越大。图4中存在一临界直径dcrit[12]，比该直径大的颗粒会发生悬浮，比该直径小的颗粒则不会发生悬浮。

3) 剩余质量比例

各阶段剩余质量比例随时间的变化如图5所示。为便于比较，将各阶段进行归一化处理。即将各阶段的开始时刻设为0，各阶段开始时刻剩余质量比例设为1。由图5可见，随着再悬浮的进行，剩余质量比例逐渐降低。随着阶段1到阶段6流体速度的提高，剩余质量比例下降得更快。这表明速度越大，悬浮得越快，即悬浮率Λ越大。而在同一流速下，悬浮质量与悬浮率和悬浮时间相关，随着悬浮的进行，大颗粒逐渐脱离固体表面，悬浮率逐渐降低，悬浮过程直到比临界直径大的颗粒全部悬浮脱离固体表面而终止。

图4 气溶胶悬浮率Fig.4 Aerosol resuspension rate

图5 剩余质量比例Fig.5 Percentage of remaining mass

4) 颗粒受力与流体速度的关系

与气溶胶再悬浮相关的受力中，只有拖曳力Fd和爆发力Fb与流体速度相关。不同速度下二者与直径的关系如图6所示，二者均随直径的增大而增大，且在全部直径范围均随流体速度而增长。

图6 拖曳力和爆发力Fig.6 Drag force and burst force

5) 计算值与试验值的比较

悬浮比例计算值与试验值的对比如图7所示。由图7可看出，试验测量得出的悬浮比例呈阶梯状增长，而计算结果呈光滑状增长，且多数时间中，悬浮比例的计算值比试验值偏大。ECART模型的特点是颗粒的悬浮质量与悬浮率和悬浮时间有关，其悬浮比例呈平滑增长。悬浮过程中，由于大颗粒的悬浮率更大而首先悬浮，直到达到该流动速度下的临界直径时悬浮终止。而在试验中，悬浮仅发生在速度变化的最初一段时间，故悬浮的测量值呈阶梯状增长。ECART模型的计算值与试验值间的差别可能因为模型下仅考虑了一定流速下单层沉积颗粒的悬浮作用，认为全部沉积颗粒都暴露在流动中，表层到深层颗粒的悬浮率相同，即模型没有模拟颗粒通过多层沉积物夹带的深度过程，使得同一流速下的悬浮率增大，最终导致同一流速下悬浮比例结果中的计算值大于试验值。ECART模型是半经验公式模型，其经验参数通过试验数据得出，在敏感性分析中可通过改变模型中的经验参数，使计算值更贴近试验值[13]。

图7 悬浮比例Fig.7 Percentage of resuspension

3 结论

利用CABSA程序再悬浮模块的ECART模型对STORM项目中的SR11试验进行了气溶胶再悬浮计算，所得结果如下。

1) 与气溶胶再悬浮相关的各分力均随直径的增大而增大，其中使气溶胶悬浮的拖曳力和爆发力比使气溶胶附着的黏着力随气溶胶直径增长得更快；存在某一临界直径，使得比该直径大的气溶胶所受悬浮力大于0而发生再悬浮，而直径越大的气溶胶越容易发生再悬浮。

2) 悬浮率与气溶胶所受悬浮力呈正比，气溶胶直径越大，悬浮率越大，越容易发生再悬浮。

3) 气溶胶沉积表面流体速度增大时，各直径颗粒的拖曳力和爆发力均变大，最终导致悬浮率的增加。

4) 气溶胶悬浮质量与悬浮率和悬浮时间相关，在沉积表面的一定流速下，悬浮发生到临界直径而停止。

在严重事故晚期，可利用气溶胶再悬浮的上述特性，通过降低气溶胶沉积表面的流体速度，降低拖曳力和爆发力，减小悬浮率，最终减小裂变产物向空间内的重新释放。