静水中单气泡运动特性实验研究

李文强，焦守华，唐 珂，杨宜昂，曲文海，柴 翔

(1.上海交通大学 核科学与工程学院，上海 200240；2.普渡大学 核工程系，美国 西拉法叶 47906)

气液两相流动和传热广泛存在于核能工程、石油工程等工业领域以及自然科学研究领域。核反应堆正常工况运行时，定位格架前后的两相流特性将大大影响反应堆燃料组件的热工水力性能[1]，当反应堆发生事故，且堆芯熔融物融穿压力容器下封头掉进堆坑内后，由于堆芯余热导致的堆坑水内两相流动特性将显著影响放射性物质的释放速率[2]。板式核燃料组件矩形流道内的流动换热研究中[3]，矩形通道内的热工特性与气泡的生成和分布密切相关，气泡的生成将极大影响矩形通道内的热工特性。在海上石油钻井平台中，气态天然气和水的混合物形成两相流动，显著增强了钻井内流动阻力，增加了海底井口的堵塞风险[4]。对气泡的运动速度、形态和轨迹特性进一步研究将有助于提高工程的安全等级或生产效率。针对单气泡上升运动特性，文献[5-11]进行了广泛的理论和实验研究，然而由于静止水中气泡运动过程存在着随机性，气泡上升轨迹对壁面与气泡发生点距离、气泡产生方法等初始条件敏感，气泡运动轨迹、变形程度和瞬时速度之间存在着复杂的相互作用，因此迄今为止仍未形成完整、通用、准确的末速度预测关系式。

本文采用高速摄像机和图像识别技术，对不同等效体积直径下气泡的运动轨迹、变形程度、瞬时速度和末速度进行研究。

1 实验装置

实验装置如图1所示，主要由气泡发生装置、实验段、光源系统、高速摄像机和图像处理程序组成。气泡发生装置由注射泵、针阀、毛细管、橡胶塞组成，注射泵采用雷弗TSD-01双向推拉型注射泵，注射速率控制范围为1 μL/min～87 mL/min，通过同步器快速切换针阀达到快速切换注射器正负行程的目的。毛细管内径分别为0.3、0.7、1、2、3、4和5 mm，采用可控缓慢生长的方式产生气泡，橡胶塞用于固定可更换的毛细管，用于产生等效体积直径为2.5～7.11 mm的气泡。为消除壁面效应影响，实验段采用200 mm×200 mm×600 mm的透明亚克力水箱组成，为保证方形水箱内具有很低的导热系数来排除外界温度变化的影响，水箱厚度达20 mm，方形水箱内为去离子水工质。实验照明系统为200 mm×200 mm的平行白色光源，背面打光。采用400帧/s的帧率拍摄气泡上升过程。本文实验条件接近Liu等[12]的实验条件，气泡脱离毛细管150 mm后，速度已充分发展，达到稳定状态，基于保守性的考虑，本文选取的拍摄中心位于管嘴出口265 mm处，测量面积为60 mm×90 mm的矩形区域。测量得到的运动图像通过图像处理程序进行处理，最终得到气泡运动瞬时坐标、瞬时速度、变形程度等相关信息。

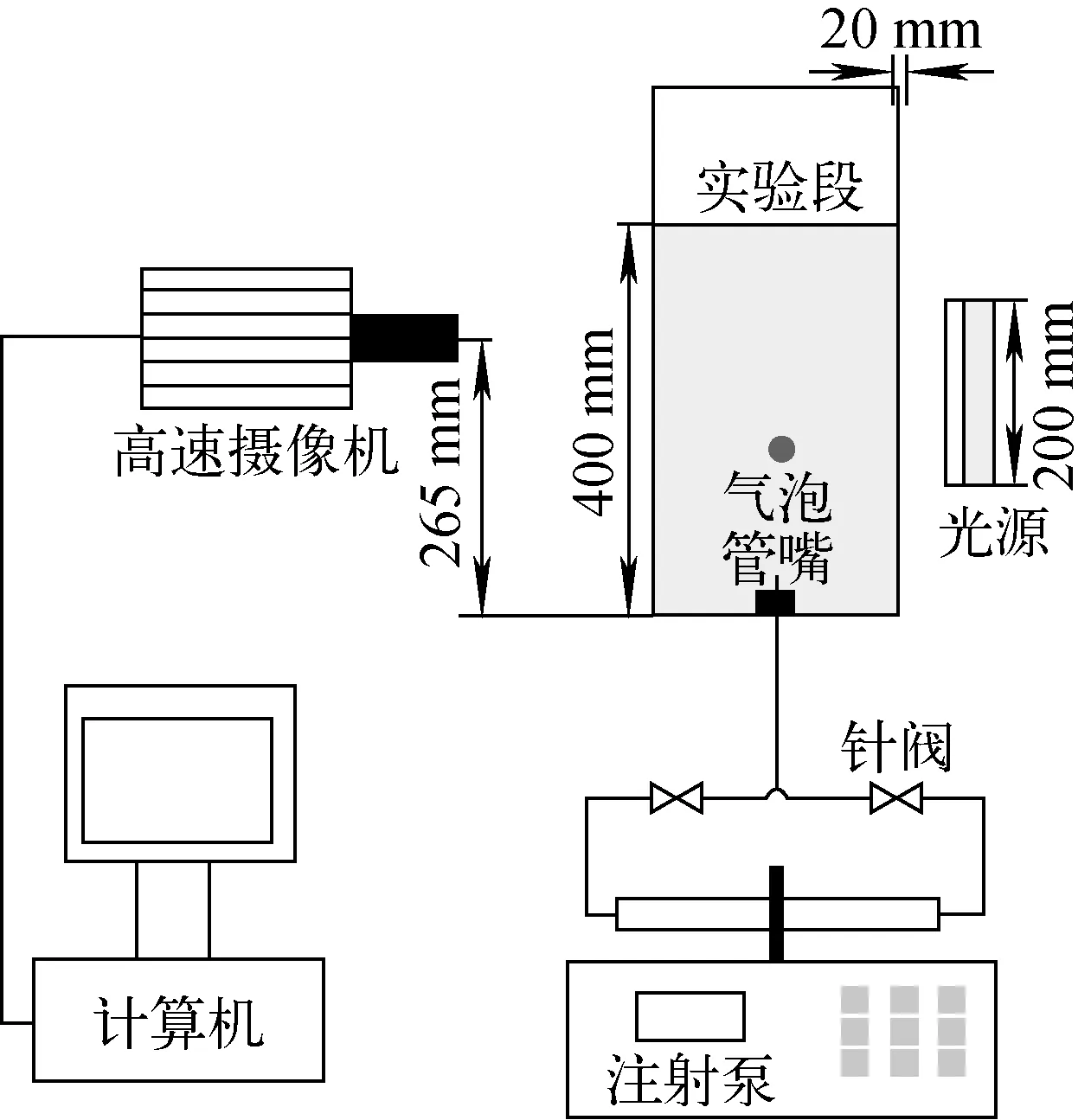
图1 实验装置示意图Fig.1 Schematic diagram of experimental system

2 图像处理技术和误差分析

2.1 图像处理技术

图形处理流程如图2所示，经过背景减除、对比度增强、边缘识别、形态学处理等过程后即可获得图3所示的气泡轮廓图像，进一步处理即可获得气泡速度、气泡变形程度和气泡等效直径等信息。计算气泡速度前先通过下式计算气泡质心：

(1)

(2)

式中：xi和zi为气泡轮廓内的所有像素坐标；X和Z为求得的气泡质心坐标；N为记录的气泡上升过程所用的总帧数。

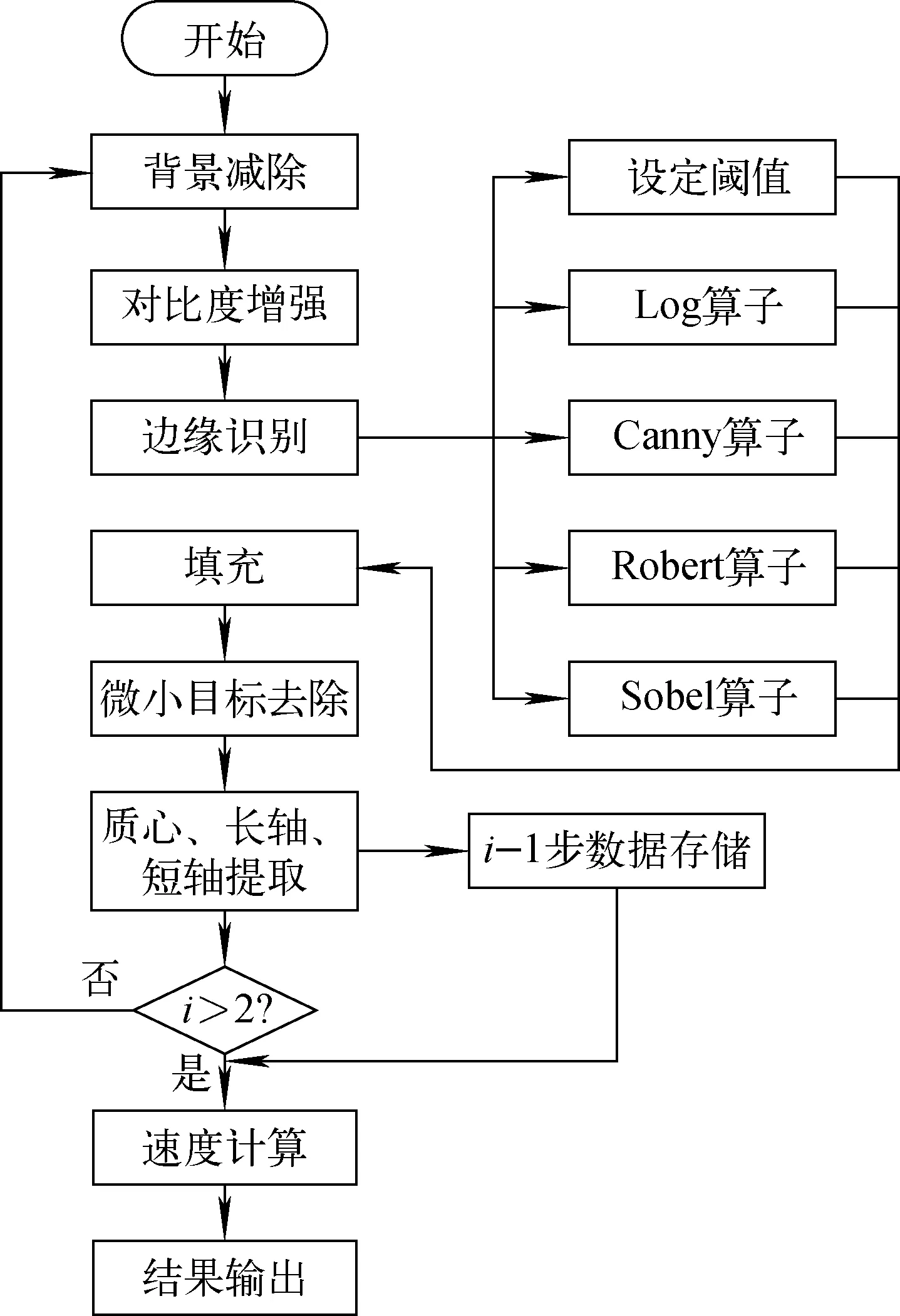
图2 图形处理流程Fig.2 Flow chart of image processing

图3 气泡的长轴短轴示意图Fig.3 Schematic diagram of bubble major axis and minor axis

气泡速度为：

(3)

(4)

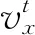
气泡的变形程度和等效体积直径均与气泡图像长轴a和短轴b有关(图3)，气泡的变形程度采用纵横比E表示：

(5)

气泡等效体积直径de采用下式计算：

(6)

不同边缘识别算法的纵横比和等效体积直径对比如图4所示，经过Canny、Robert、Sobel、Prewitt边缘算子得到的纵横比和等效体积直径差异很小，不同算子的图像处理过程对后续得到气泡运动参数敏感性很小，因此理论上4种算子均可采用。鉴于Canny算子通常具有更强的抑制噪声的能力[13]，本文选择Canny算子。

2.2 气泡运动参数不确定度分析

借鉴Celata等[14]和Zhang等[15]气泡运动参数不确定度处理方法，对气泡末速度、纵横比和等效体积直径进行不确定度分析。图像识别过程中，气泡边缘处某个方向上多识别或少识别1个像素所造成的质心不确定度为±0.5像素，气泡长轴和短轴的识别不确定度为±1像素。

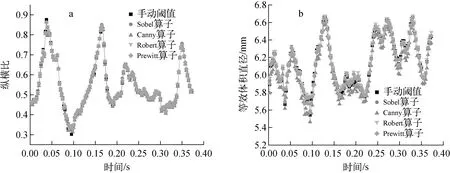
图4 不同边缘识别算法的纵横比(a)和等效体积直径(b)的对比Fig.4 Comparison of aspect ratio (a) and equivalent volume diameter (b) for different edge detection algorithms

根据不确定度传递公式，气泡末速度的绝对不确定度εu为：

εu=

(7)

式中：u为气泡末速度；Z1、Z2分别为气泡前后两帧的像素坐标。

气泡等效体积直径不确定度εde和纵横比不确定度εE分别为：

(8)

(9)

根据以上分析方式得到了气泡末速度、等效体积直径和纵横比的相对不确定度分别为0.67%、2.17%和4.63%，所有参数的相对不确定度均小于5%。

3 实验结果和讨论

3.1 气泡运动轨迹和变形程度

图5示出不同等效体积直径气泡运动的轨迹。由图5可见，不同等效体积直径的气泡在上升过程中受到空间不对称的湍流涡脱离的影响，运动轨迹呈现出不同振荡幅度的运动形态，等效体积直径小于5 mm的气泡呈现出螺旋形运动，等效体积直径大于5 mm的气泡逐渐变为Z字形运动。

气泡在浮力作用下开始逐渐加速到末速度状态，受到阻力和浮力影响，气泡上部与下部存在一较大的压力差，压力差作用下气泡底部形成涡环并引导射流向上运动引发气泡变形。气泡直径越大，Eo越大，气泡顶部和底部诱导出的压力差越大[16]，气泡底部射流越大，而表面张力越弱，表面张力引起的气泡内部附加压强越小，因此气泡变形越大。由图5不难发现，气泡直径越大，变形程度越明显。

3.2 气泡振荡幅度、瞬时速度和瞬时纵横比

单气泡上升过程中变形程度、瞬时速度、运动轨迹之间存在复杂的相互耦合关系，气泡变形程度的瞬时变化程度会影响气泡上升过程中曳力受力面积，受力面积的瞬时变化进而会影响气泡在横向和纵向运动的速度，气泡横向运动的瞬时变化速度会影响气泡上升过程中气泡横向迁移的轨迹，气泡纵向速度的瞬时变化会影响曳力大小，而曳力大小瞬时变化将改变气泡运动过程中的受力平衡，最终影响气泡变形程度。

图6示出不同等效体积直径下气泡的横向振荡幅度，图7示出不同等效体积直径下气泡瞬时速度与瞬时纵横比的对比。由图6、7可见，气泡等效体积直径为2.51 mm时，气泡横向速度振荡幅度为150 mm/s，横向振荡幅度为6 mm，当气泡直径增加到6.86 mm时，气泡横向速度振荡幅度为130 mm/s，横向振荡幅度为3 mm，因此气泡横向振荡幅度与横向速度vx峰值呈正比。

由图7可见，气泡等效体积直径由2.51 mm逐渐增加至6.86 mm时，气泡瞬时纵横比振荡幅度由0.075增大至0.2，气泡的瞬时纵向速度vz的振荡幅度由12.5 mm/s增大至50 mm/s，气泡瞬时横向速度振荡幅度由150 mm/s降低至130 mm/s。这表明，小直径气泡的瞬时纵横比振荡幅度较小，气泡瞬时横向速度振荡幅度较大，瞬时纵向速度振荡幅度较小；大直径气泡瞬时纵横比振荡幅度较大，气泡瞬时横向速度振荡幅度较小，而气泡瞬时纵向振荡频率较大。其原因为气泡直径增大后，表面张力对气泡变形程度的影响逐渐变弱，气泡周围流场的变化更容易导致气泡发生大幅度的变形，气泡瞬时纵横比的振荡幅度增大，气泡的变形程度最终影响了气泡横向速度的变化。从不同直径下气泡瞬时横向速度、瞬时纵向速度及瞬时纵横比的变化频率来看，气泡纵向运动频率和纵横比变化频率为气泡横向运动频率的两倍，不随直径的变化而发生变化。同样不难发现，气泡瞬时纵横比的大小与瞬时纵向速度之间呈反比关系，这种反比关系可根据Moore[17]的理论进行解释：气泡速度越大，气泡顶部的动压更强，因此变形程度更大，瞬时纵横比越小；反之气泡速度越小，气泡顶部的动压更弱，因此变形程度更小，瞬时纵横比越大。

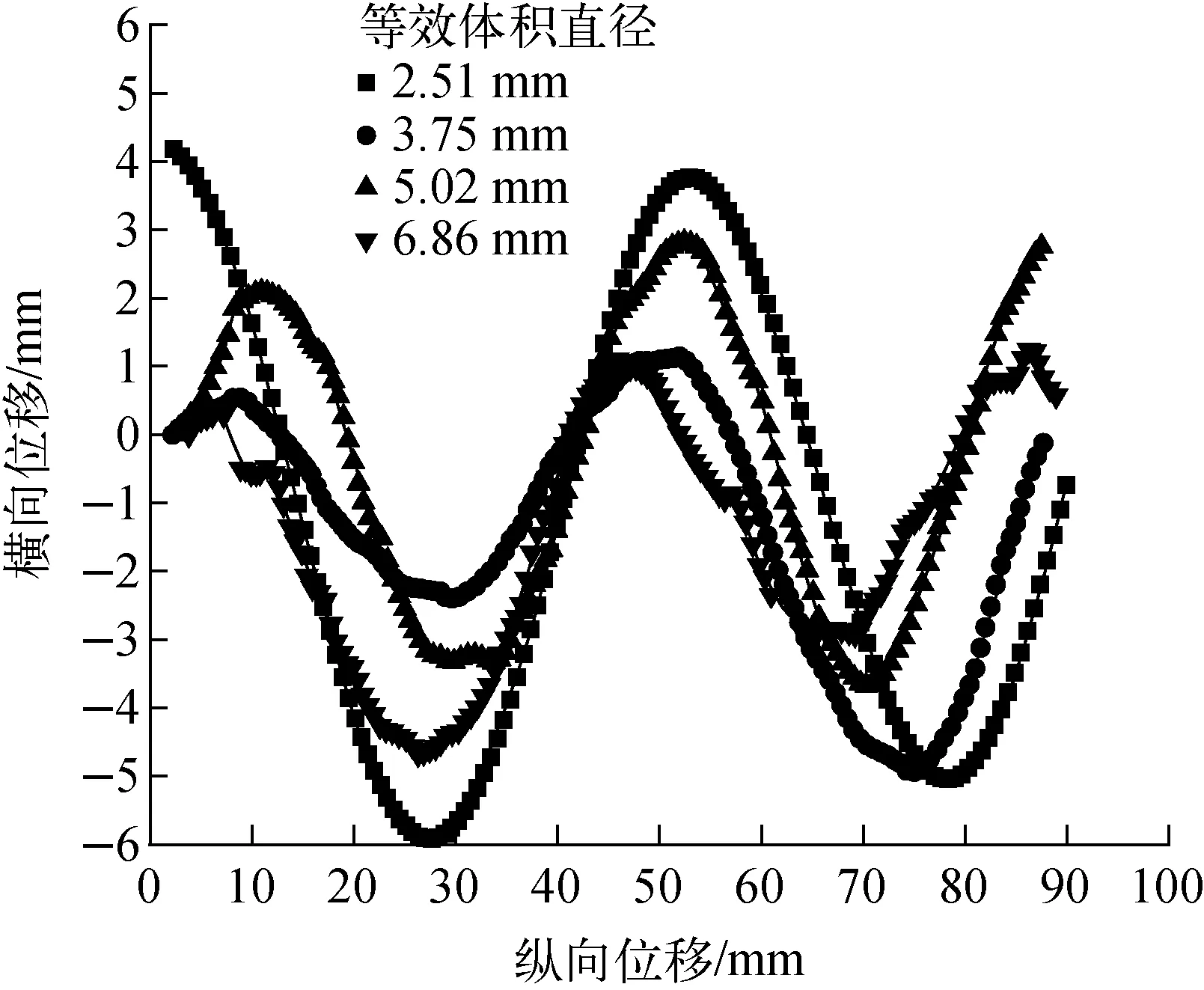
图6 不同等效体积直径下气泡的横向振荡幅度Fig.6 Bubble axial oscillation amplitude for different equivalent volume diameters

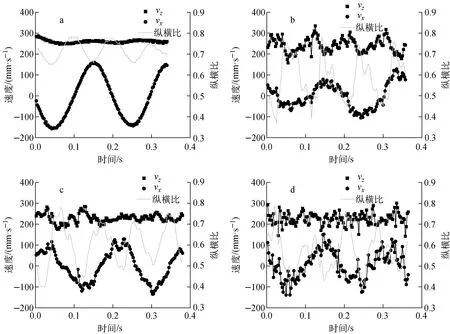
等效体积直径：a——2.51 mm；b——3.75 mm；c——5.02 mm；d——6.86 mm图7 不同等效直径下气泡瞬时速度与瞬时纵横比的对比Fig.7 Comparison of bubble instaneous velocity and instaneous aspect ratio under different equivalent volume diameters

图8示出气泡横向位移、横向速度和纵横比的对比，图9示出气泡运动坐标示意图。由图8、9可见：当气泡速度从0逐渐加速到速度最大时，气泡的纵横比逐渐变小，气泡逐渐接近椭球形，位置越接近中轴线。根据Fan等[18]的研究结果，气泡在上升过程中下表面附近形成了不对称的湍流涡，其周期性从气泡表面脱落，影响了气泡周围流场的分布和气泡受力，从而造成上升速度和气泡横纵比周期性变化。

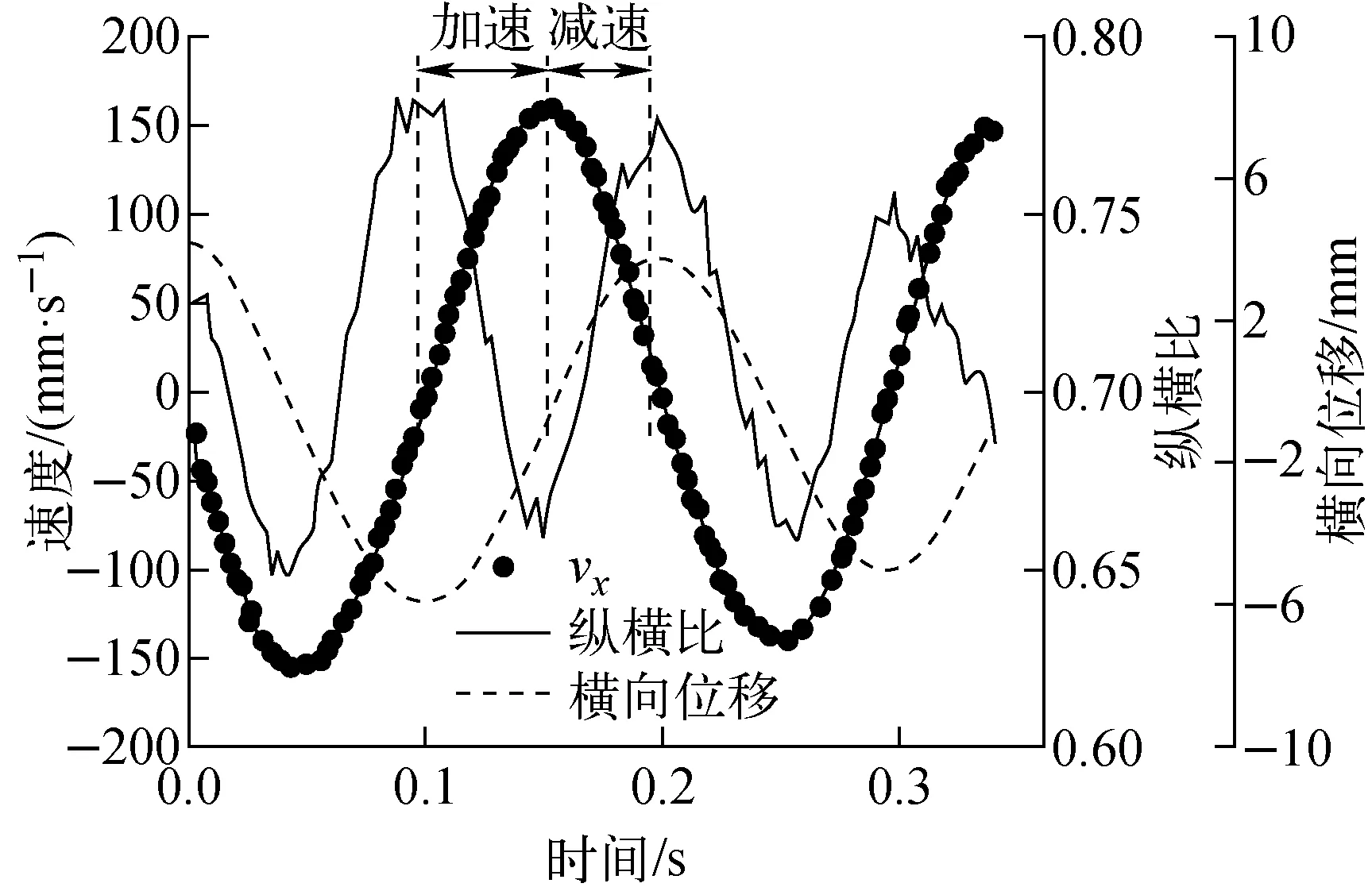
图8 气泡横向位移、横向速度和纵横比示意图Fig.8 Schematic diagram of lateral motion,lateral velocity and aspect ratio of bubble

3.3 气泡末速度与等效体积直径的关系

在工程应用领域，更关注的是气泡的末速度vT，在分析气泡末速度时，多数学者仅考虑浮力和曳力：

(10)

式中：g为重力；ρL、ρg分别为水和气体的密度；Cd为曳力系数。

图9 气泡运动坐标示意图Fig.9 Schematic diagram of bubble motion coordinate

气泡末速度由重力、气液密度之比、等效体积直径、曳力系数共同决定。其中：Rybczynski[5]从理论出发推导出了Re小于1的适用于球形气泡的运动末速度关系式；Wallis[6]将该关系式推广到Re介于1～100之间，适用于微变形的球形气泡；考虑到气泡运动过程中存在的巨大变形，Davies等[7]推导得到了一个半经验末速度运动关系式；Mendelson[8]从波动理论出发，得到了气泡直径介于1.4～6 mm之间的末速度理论关系式；Tomiyama等[10]从势流理论出发，推导得到了纯净水中气泡末速度与气泡纵横比、气泡直径和物性的显式关系式；Park等[11]总结了文献中不同直径下单气泡运动末速度实验数据，获得了气泡末速度与气泡直径、物性之间的通用显式关系式。

图10示出不同等效体积直径下气泡末速度的对比。由图10可见，Rybczynski、Davies等的关系式在预测等效体积直径为2～8 mm的气泡末速度时，预测值与实验值存在100%以上的相对误差，不再适用。Mendelson的关系式在预测小直径气泡末速度关系式时存在过高估计，直径越小，误差越大。Wallis的关系式在预测等效体积直径为2～5 mm的气泡末速度时，存在20%左右的相对误差。Tomiyama等的关系式低估了单气泡运动在等效体积直径为2～8 mm之间的末速度，这与Tang[19]的结论一致。Park等的显式关系式与实验值相比偏高，其主要原因为该关系式采用函数构造的方式获得，通过抑制因子fsc来调节水中杂质对球形气泡区域阻力系数的影响，而在纯净水中Park等认为fsc=1。

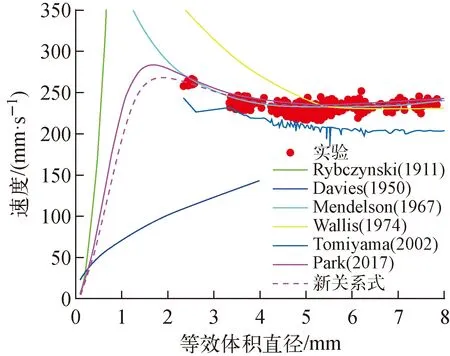
图10 不同等效体积直径下气泡末速度的对比Fig.10 Comparison of bubble terminal velocity with different equivalent volume diameters

为获得更加通用的精确显式关系式，借鉴Park等的关系式重新构建一新的显式关系式，引入A2和B2两个参数修正关系式中的分母，并根据实验数据拟合出如下关系式：

(11)

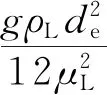
采用均方根误差RMS来衡量各关系式间的预测精度，其定义如下：

(12)

式中：vei为实验获得的气泡末速度；vsi为通过关系式拟合得到的气泡末速度。经计算，新关系式、Park、Tomiyama和Wallis等的关系式的RMS分别为2.75%、3.63%、10.01%和20.12%，新关系式的RMS明显更小。因此在纯净水中，新关系式在预测等效体积直径介于2～8 mm之间的气泡末速度时精度更高。

4 结论

针对单气泡上升过程，本文从气泡运动轨迹、气泡瞬时速度、气泡瞬时纵横比、气泡末速度等方面对气泡运动特性进行了研究，研究结论如下。

1) 气泡横向振荡幅度与气泡横向速度峰值呈正比，两者均随气泡等效体积直径的增加而降低。

2) 气泡瞬时纵横比变化频率与气泡瞬时纵向速度变化频率一致，是气泡瞬时横向速度变化频率的两倍，与气泡等效体积直径无关。

3) 随气泡等效体积直径增大，气泡瞬时纵横比振荡幅度不断加大，瞬时横向速度振荡幅度不断减小，纵向速度振荡幅度减小。

4) 大多数气泡在横向偏移为0时横向速度趋向于最大值，纵横比趋向于最小值，反之亦然。气泡下表面涡的不对称脱离是导致气泡纵横比、上升速度、横向位置周期性变化的原因。

5) 气泡纵横比大小与纵向速度大小呈反比关系，即气泡纵横比最大时气泡纵向速度最小，气泡纵横比最小时气泡纵向速度最大。

6) 本文针对气泡末速度关系式目前绝大多数为隐式关系式的弊端，提出了兼顾精确性和便利性的显式关系式，新关系式的RMS明显更小。