窄矩形通道两相流动沸腾压降特性实验研究
孙汝雷,张大林,周健成,宋功乐,田文喜,苏光辉,秋穗正
(1.西安交通大学 核科学与技术学院,动力工程多相流国家重点实验室,陕西 西安 710049;2.陕西省先进核能技术重点实验室,陕西 西安 710049)
板型燃料元件具有结构紧凑、体积功率密度高、燃耗高等优点[1],在先进研究堆和舰船核动力装置中广泛应用。由于相邻燃料板间隙通常为1~3 mm,且具有较大的宽高比,因此其内部冷却剂的两相流动沸腾特性与常规管道明显不同。近年来,国内外研究人员针对大宽高比的窄矩形通道内的单相和两相流动换热特性进行了一系列研究[2-6],但两相研究主要针对气-水或制冷剂为工质,因此对于蒸汽-水系统的适用性还有待进一步验证。另外,由于自屏效应及堆内布置形式的影响[7-8],板型燃料元件沿宽度方向上的功率分布不均匀,并且这种不均匀性还会随轴向位置和反应堆的工作条件发生变化。横向功率分布不均匀性必然会影响气泡核化位置及气泡运动特性,从而对两相流动压降产生影响。目前对于矩形通道横向非均匀加热条件下两相流动沸腾特性的研究较少,主要是在韩国[9-11],且其研究也主要是针对核态沸腾起始点、流动不稳定性等。
本文实验研究横向均匀和非均匀加热条件下窄矩形通道内两相流动沸腾压降特性,基于实验数据对现有关系式的适用性进行评价,并在此基础上提出改进形式的关系式。
1 实验装置和实验段
1.1 实验系统
本研究在西安交通大学核反应堆工程热工水力实验室开展,实验系统如图1所示,主要由主回路和冷却回路组成。主回路设计为开式回路,由水箱、柱塞泵、回热器、预热器、实验段、冷凝器、测量仪表、阀门和管道等组成。实验工质为去离子水,回路最大流量为2 t/h。冷却回路主要由冷却水箱、循环泵、冷却塔及其他阀门和管线组成。实验流程为常压过冷水由水箱流出经柱塞泵做功升压后,经流量调节和测量模块后进入回热器吸收流出实验段工质的废热,并通过预热器进一步加热至实验要求的入口状态,流入实验段;从实验段出来的高温水依次经回热器和冷凝器后回到水箱。
1.2 实验段
实验段设计为双面加热,包括矩形通道、加热元件、导热铜块、出入口变径接管、绝缘板、支撑结构和测量模块(图2a)。矩形通道的横截面为2 mm×60 mm,长度为1 000 mm。有效加热部分长度为700 mm,宽度为56 mm。考虑到实际板型燃料元件包壳的影响,两侧各留有2 mm宽的非加热区(图2b)。入口和有效加热段之间留有145 mm长的非加热段,使流体在进入有效加热区之前得以充分发展。同样地,在加热段和出口之间留有相同的距离,以减少出口尾流对加热区的影响(图2a)。
实验段两侧对称布置5组平行放置的加热元件,加热元件由Ni20Cr80高强度电热合金制成。在每个加热元件与矩形通道壁之间放置高纯度无氧铜块,沿铜块轴向上切割有若干气隙以阻止轴向热传导。每个铜块沿轴向上布置6组测温热电偶,每组放置两个直径1.5 mm的K型热电偶,间距为8 mm(图3)。在铜块和电加热元件之间放置0.5 mm厚的高导热氮化铝陶瓷片进行绝缘。此外,在铜块、氮化铝陶瓷片和发热元件之间,以及铜块和通道壁之间涂覆一薄层高温无机导热填料,降低界面接触热阻。距离有效加热段两端15 mm处各设置1组热电偶测量出入口流体温度,采用罗斯蒙特压力和差压变送器测量实验段的入口压力和压降,采用NI数采系统和基于LabVIEW的程序接口对实验数据进行采集和存储,测量参数及其不确定度列于表1。
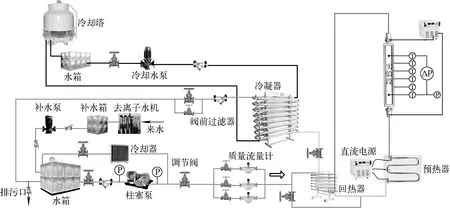
图1 实验回路系统图Fig.1 Schematic of experimental loop

a——实验段装配图;b——流道截面示意图图2 实验段示意图Fig.2 Details of test section

图3 测点布置图Fig.3 Schematic diagram of measuring point

表1 测量参数及其不确定度Table 1 Measurement parameter and instrument uncertainty
2 实验参数和数据处理
2.1 实验参数
实验用去离子水电导率<0.8 μS/cm,实验中调节旁通阀开度和泵频率对流量进行调节,系统压力由回路的背压阀调节。首先调节预热器的加热功率,将实验段入口温度控制在相应入口压力下饱和温度的0.5 ℃偏差范围内,然后逐渐调整实验段的加热功率,使其达到设定值。当5 min内出入口温度变化在±0.1 ℃、压差在±0.1 kPa范围内时,认为系统达到稳态。然后以1 kHz的采集频率记录流量、入口压力、压差和温度信号,持续5 min。
选取3种典型的加热功率分布研究横向加热功率分布的影响,结果如图4所示,图中曲线为理想状态,阶梯线为实验加热功率分布。

图4 横向加热功率分布曲线Fig.4 Heating power distribution profile
横向无量纲功率分布因子:
P*=P/P均匀
(1)
均匀功率分布:
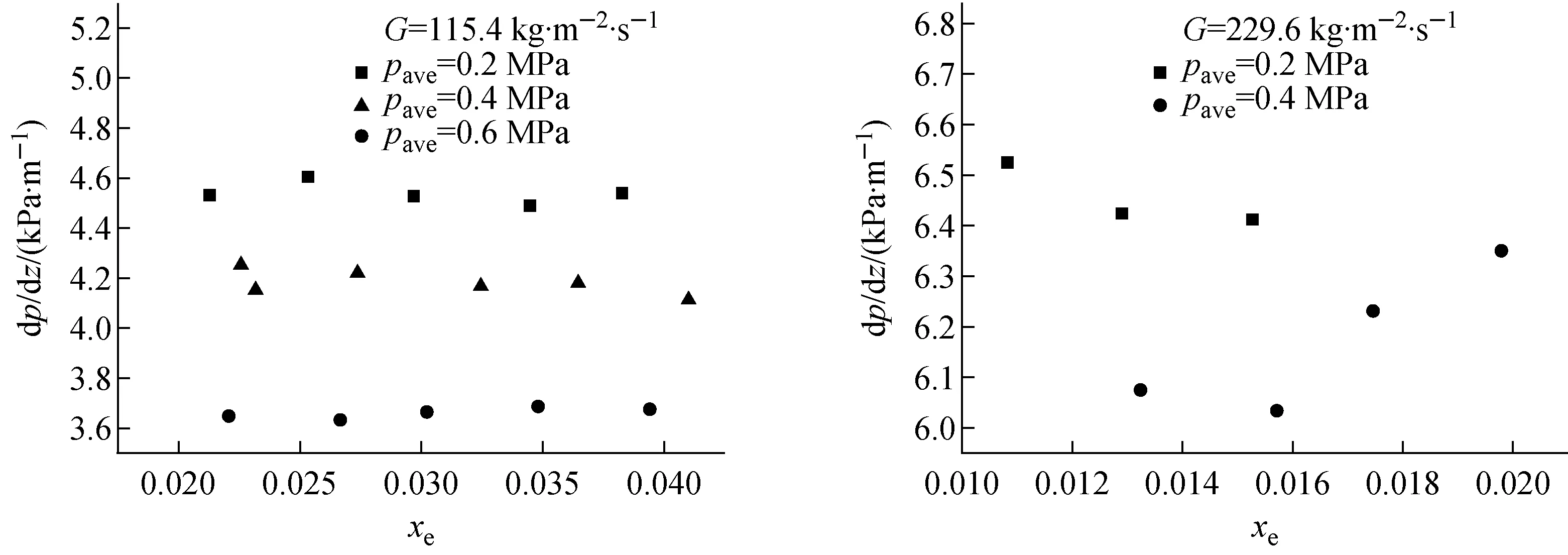
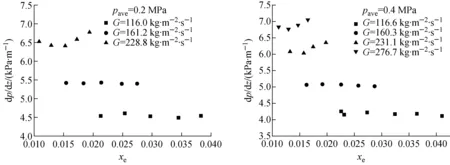
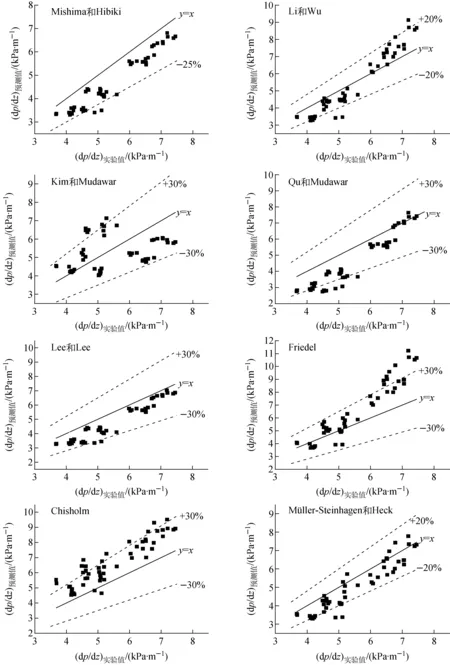
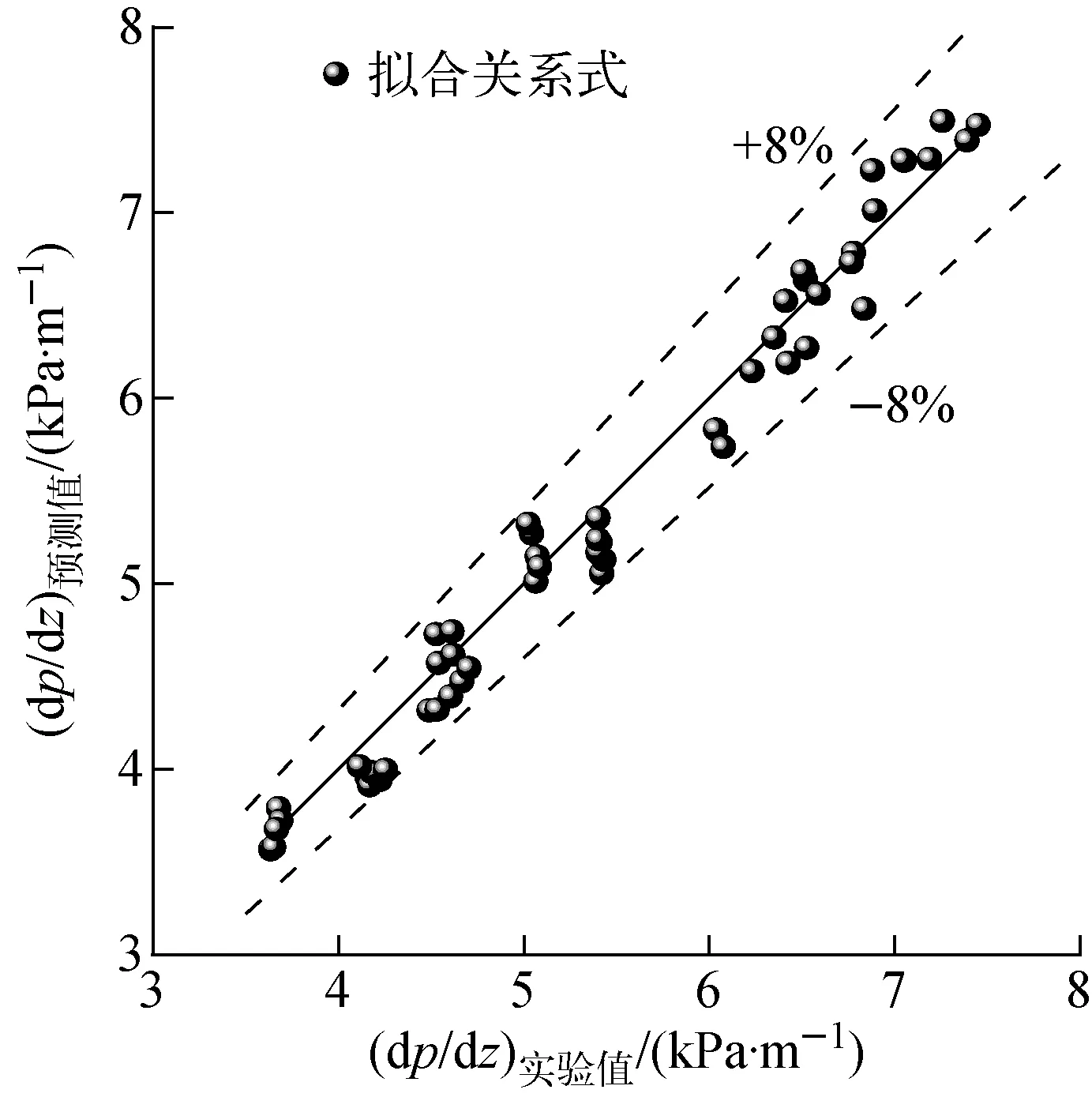
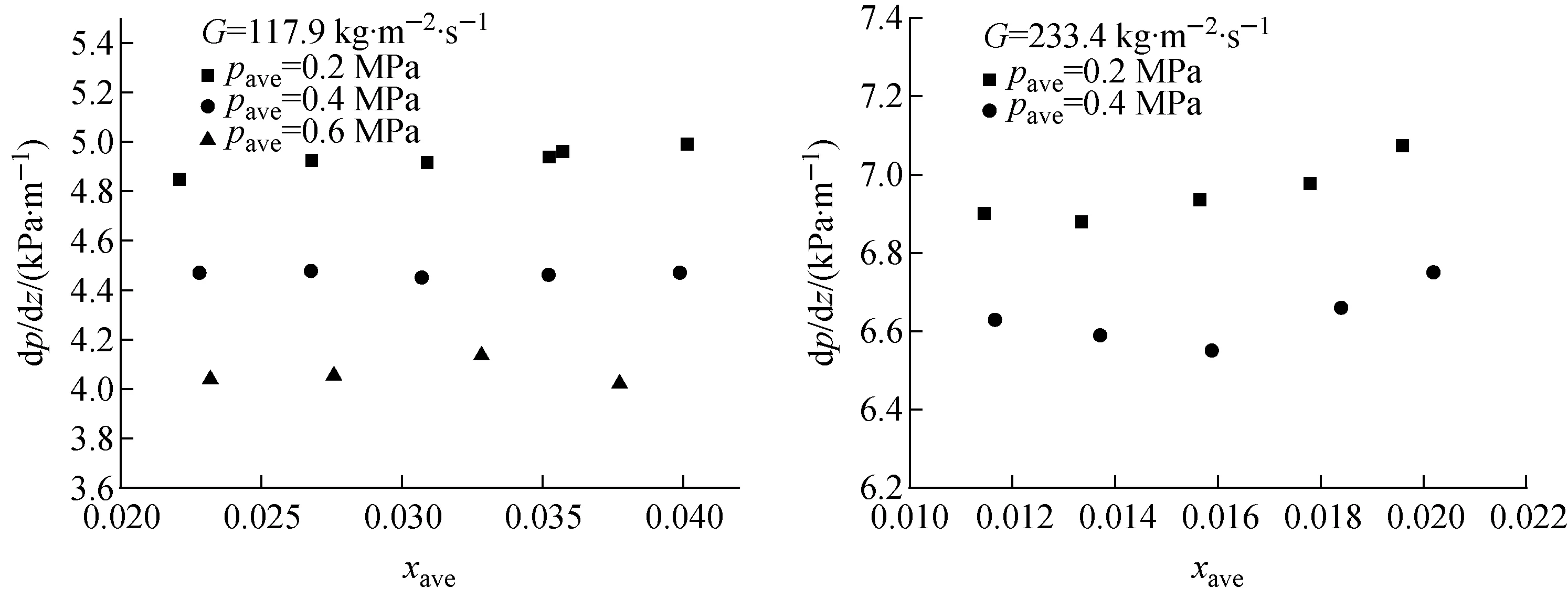
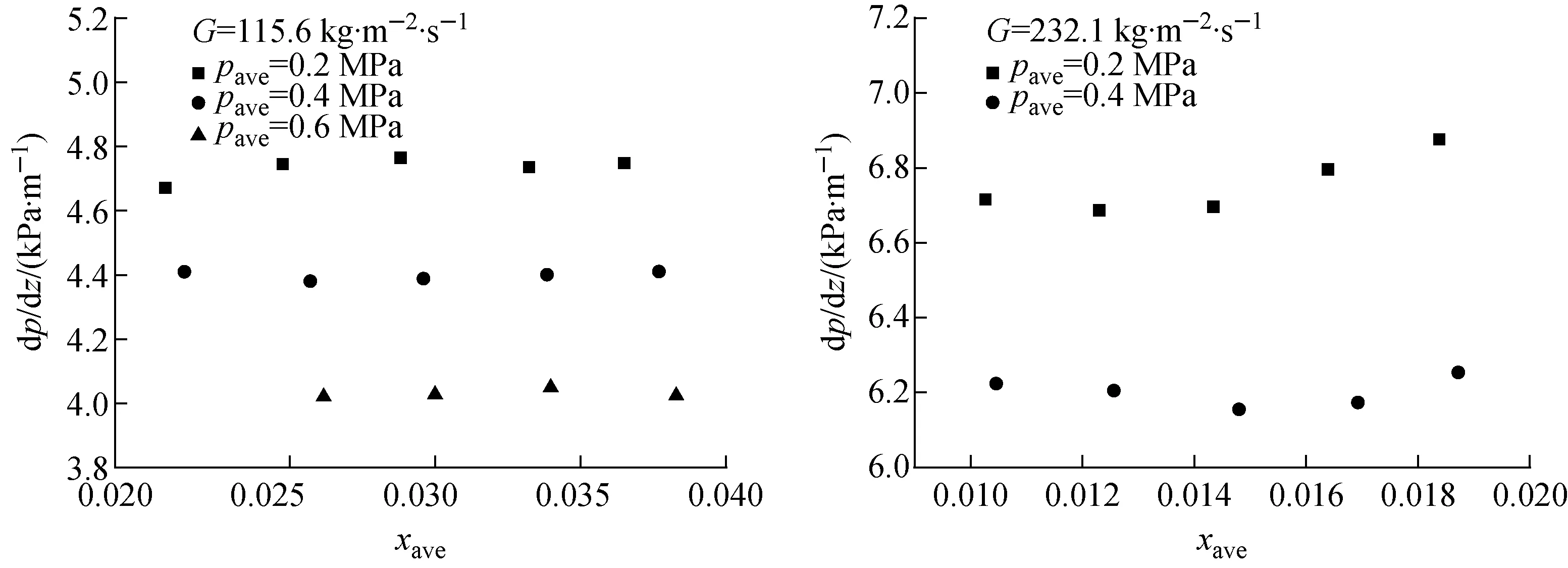
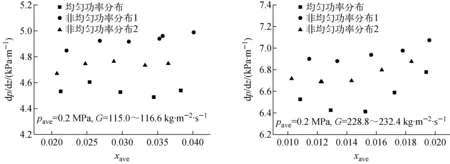
P*=1-2.8 cm (2) 非均匀功率分布1(正弦分布): -2.8 cm (3) 非均匀功率分布2(多项式分布): P*=0.001 1x6+0.000 4x5-0.004 4x4- 0.003 1x3+0.047 9x2+0.038 7x+0.846 1 -2.8 cm (4) 3种功率分布形式的选择依据和标准为:首先,均匀功率分布是传热研究中最常见和最基本的壁面边界条件之一,且广泛用于许多复杂问题的近似处理。如在反应堆的热工水力研究中,多数现有实验研究和商用分析程序(RELAP5和COBRA等)均假设板状燃料元件的横向功率是均匀分布的。在本研究中,均匀功率分布还作为与非均匀功率分布比较的基础。其次,非均匀功率分布1(正弦分布)通常出现在核燃料元件轴向功率分布的假设中,且在微通道散热器和辐射散热器[12]领域,在垂直冷却剂流动方向上也存在相似的热通量分布。最后,非均匀功率分布2(多项式分布)的选择是基于板型燃料元件的精细物理计算,Jo等[13]基于MCNP分析结果拟合得到板型燃料元件横向上的6阶多项式功率分布,其他研究人员在研究报告中也提到了类似的分布(Wilson等[14]和Meyer[15])。因此,选择此3种功率分布进行研究,以便为反应堆燃料元件和其他工业热交换器的设计和分析提供帮助。 实验基于单变量原则,确保对比实验中3种功率分布沿横向和轴向上的总积分功率一致,实验段每侧加热面设置相互独立的5个电加热元件,前、后两个加热面上相对的两个加热元件为1组,由同1个电源模块按并联方式加热,因此整个实验段共有5个独立的电源模块。实验过程中可根据预先设计的加热功率分布,分别调节每个电源模块的输出功率,完成实验研究。实验参数范围列于表2。 表2 实验参数范围Table 2 Range of experiment parameter 根据动量守恒定律可得到: Δpf=ΔpDP+Δpg,DP-Δpg-Δpa (5) 式中:ΔpDP、Δpg,DP分别为差压变送器测量值和引压管内流体重位压降;Δpg为引压管间实验段内流体重位压降;Δpa为流体加速压降;Δpf为摩擦压降。 加速压降均相流模型: (6) 加速压降分相流模型: (7) 实验段重位压降: (8) 引压管重位压降: (9) 本文空泡份额的计算采用Smith模型[16],ψ=0.4。 (10) 轴向不同位置局部含气率: (11) 1) 参数分析 图5为不同饱和压力pave下两相压降梯度dp/dz随热平衡含气率xe的变化。在一定的质量流速和含气率下,随饱和压力的增大,压降梯度明显减小。这是由于随着饱和压力的增大,液体密度略有减小,饱和蒸汽密度显著增大,从而混合物密度增大,重力压降分量增大;但由于蒸汽-水密度差和黏性差显著减小,导致两相速度差减小、相间黏性剪切应力减小,从而摩擦压降分量显著减小;加速压降分量随饱和压力的变化非常小,因此综合效应表现为两相压降随饱和压力的增大而减小。 图6为不同质量流速下的两相压降梯度随热平衡含气率的变化。在一定的压力和含气率下,随着质量流量的增加,重力压降分量和加速压降分量几乎不变,摩擦压降分量增加(图7b),因此总的两相压降梯度明显增大,这与传统圆管的结论一致。另外,图5、6均反映了在低质量流速下,两相压降梯度几乎不随含气率发生变化。因为在较低的质量流速和含气率下,两相之间的扰动较弱。随含气率的增加,虽然加速压降和摩擦压降略有增加,但重力压降减小。叠加效应表现为两相压降梯度几乎不发生变化。 图5 两相压降梯度随含气率和饱和压力的变化Fig.5 Two-phase pressure drop gradient variations with vapor quality and saturated pressure 图6 两相压降梯度随含气率和质量流速的变化Fig.6 Two-phase pressure drop gradient variations with vapor quality and mass flux 在高质量流速下,存在1个临界含气率xcr。当xe 2) 关系式评价 本文分别采用均相模型、分相模型和其他经验关系式进行预测,并与实验结果进行比较。图8为均相模型两相压降梯度预测值与实验值的比值随平均含气率xave的变化,其中等效黏度关系式分别为McAdams[17]、Cicchitti等[18]、Dukler等[19]、Akers等[20]、Beattie 和Whalley[21]、Lin等[22]和Garcia等[23]。图中显示预测值明显低估了实验值,且数据分散度较大。这是因为本研究参数为低压、低质量流速,液体和蒸汽密度很大,同时,由于窄矩形通道内气泡的生长受间隙尺寸的限制,气泡易扭曲变形,流型也易过渡为弹状流、块状流甚至环状流。因此,两相间的滑移速度较显著,相间界面摩擦引起的耗散也不容忽视。表3列出了不同等效黏度关系式计算值和实验值的误差分析结果,Beattie和Whalley关系式的预测性较好,MAE=27.1%,RSME=31.7%。因此,基于混合物等效黏度假设的均相模型对使用环境有严格的限制,高压和较大质量流速下可能有较好的预测效果,但对于低压和低质量流速,预测结果通常不是很好。 表4列出了分相模型和其他经验关系式的预测误差分析结果,图9为几个关系式的预测压降梯度与实验值的比较。其中,Müller-Steinhagen和Heck、Li和Wu关系式的预测效果最好,MAE分别为11.8%和12.3%,预测值与实验值的相对误差在±20%以内。其次是Lee和Lee、Mishima和Hibiki关系式,MAE分别为14.4%和14.7%。然而两种关系式的预测值均低估了实验值。此外,Kim和Mudawar、Qu和Mudawar、Friedel、Chisholm关系式的MAE值较接近,分别为18.0%、19.4%、20.1%和22.5%。Zhang等、Lee等、Tran等、Hwang和Kim、Zhang和Webb关系式的预测误差较大。尤其,Zhang和Webb关系式的预测MAE高达261.9%,这是由于水的对比压力远小于制冷剂和甲醇,导致其物理性质差异较大。因此单纯的基于1种或几种工质下的两相实验数据开发的关系式在应用于其他工质时需仔细评估。 图7 两相压降分量随热工参数的变化Fig.7 Two-phase pressure drop component as a function of thermal parameter 图8 均相模型压降梯度预测值和实验值比较Fig.8 Ratio of calculated and experimental values of pressure drop gradient with homogeneous model 表3 矩形模型预测结果统计分析Table 3 Statistical analysis of homogeneous model 表4 分相模型预测结果统计分析Table 4 Statistical analysis of separated flow model 图9 分相模型压降梯度预测值和实验值比较Fig.9 Comparison of calculated and experimental pressure drop gradients with separated flow model 3) 新关系式拟合 根据上述评价结果,在Müller-Steinhagen和Heck公式的基础上,提出了改进的关联式。新关系式中考虑了表面张力σ的影响,因为在微/小通道等受限流动中,表面张力的影响将变得更明显。 (B-A)Cx(1-x)1/3 (12) 1) 参数分析 图11~13示出了非均匀功率分布1和2下两相压降梯度随热力学平衡含气率、饱和压力和质量流速的变化,参数的影响趋势和均匀加热的基本一致。压降梯度随饱和压力的增大而减小,随质量流量的增大而显著增大。此外,在低质量流速时,随着含气率的增加,压降梯度基本保持不变或略有下降,而在高质量流速时,开始略有下降,然后迅速上升。 图10 拟合关系式预测值和实验数据比较Fig.10 Comparison of predicted values and experimental data 2) 与均匀加热对比 图14为两相压降梯度随含气率和横向加热功率分布方式的变化。尽管实验段总加热功率相等,横向功率分布形式对流动沸腾压降仍有重要影响。在本文研究的3种加热功率分布方式中,非均匀功率分布1的压降梯度最大,其次是非均匀功率分布2,均匀分布时的压降梯度最小。这是由于不同加热功率分布形式导致了流道内壁面温度分布的差异,从而对截面上空泡分布和横向流动产生影响(图15、16)。对于非均匀功率分布1,壁温中间高、两边低,气泡首先会在中间生成并聚合,同时受矩形通道间隙尺寸的限制,气泡容易发生扭曲变形占据较大的中心区域。随着中心区域气泡的不断产生和融合,导致同一横截面上局部压力不平衡,促使部分流体由中心区域向两侧横向流动。对于非均匀功率分布2,壁温两边高、中间低,气泡首先会在两侧区域生成和聚合,且由于窄间隙的限制,气泡挤压变形占据较大区域。类似地,横截面上有一显著的压力梯度,驱使部分流体由两侧向中心区域流动。由图4还可看出非均匀功率分布1相比功率分布2更为陡峭,无量纲功率因子大于1的部分所占面积更大。因此,在非均匀功率分布1下气泡可更早生成和聚合,从而引起的横向流动强度更大。另一方面,非均匀功率分布1和2导致的横向流动方向是相反的,角部区域流体受到的黏性耗散和剪切应力要大于中心区的,因此非均匀功率分布1的压降损失要大于非均匀功率分布2的。对于均匀加热,横向上壁温分布较为均匀,气泡几乎在整个横截面上均匀生成和分布,相同情况下,局部不易产生气泡聚集和融合形成大的气弹,横截面上压力分布更均匀,有效减少了横向上流体的流动和搅混,因而其压降梯度最小。 图11 非均匀功率分布1下两相压降梯度随含气率和饱和压力的变化Fig.11 Two-phase pressure drop gradient variations with vapor quality and saturated pressure under non-uniform power distribution 1 图12 非均匀功率分布2下两相压降梯度随含气率和饱和压力的变化Fig.12 Two-phase pressure drop gradient variations with vapor quality and saturated pressure under non-uniform power distribution 2 图13 非均匀功率分布下两相压降梯度随含气率和质量流速的变化Fig.13 Two-phase pressure drop gradient variations with vapor quality and mass flux under non-uniform power distribution 图14 两相压降梯度随含气率和功率分布方式的变化Fig.14 Two-phase pressure drop gradient variations with vapor quality and heating power distribution 图15 长度方向第3排热电偶流道内壁面温度横向分布Fig.15 Inner wall temperature distribution in transverse direction at the third row of thermocouples along length 图16 流道截面空泡分布和横向流动示意图Fig.16 Schematic diagram of void distribution and transverse flow in cross section of channel 1) 压降梯度随饱和压力增大而减小,随质量流量增大而显著增大。此外,在低质量流速时,随含气率的增加压降梯度基本不变,而在高质量流速时,随含气率的增加压降梯度先略有下降后迅速上升。 2) 利用实验数据对现有的均相、分相和经验拟合压降关系式进行了评价。采用等效黏度假设的均相模型明显低估了实验值,且数据离散度较大。经验关系式Müller-Steinhagen和Heck、Li和Wu关系式的预测性能最好,MAE分别为11.8%和12.3%,且大多数预测值在±20%的误差范围内。 3) 基于Müller-Steinhagen和Heck关系式,引入Bo考虑表面张力的影响,拟合得到一个新的两相压降预测关系式,实验数据的预测误差在±8%以内。 4) 横向功率分布对流动沸腾压降有重要影响。在本研究中,非均匀功率分布1的压降梯度最大,其次是非均匀功率分布2,均匀功率分布下的压降梯度最小。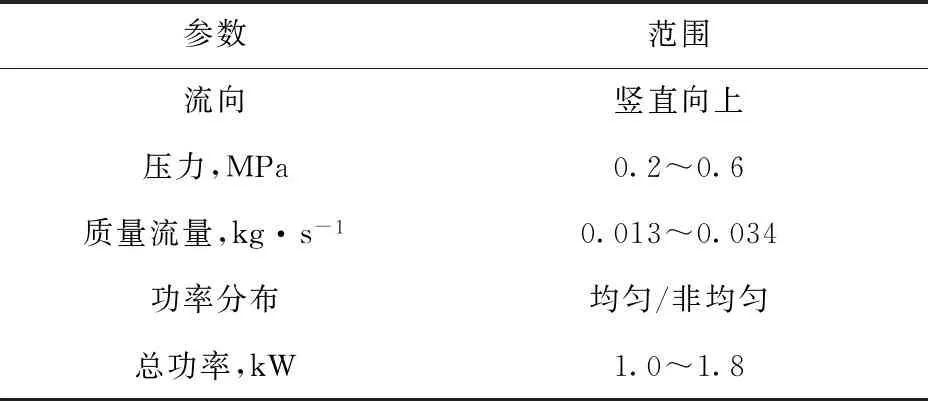
2.2 数据处理

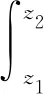

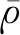

3 实验结果分析和讨论
3.1 均匀加热两相压降特性




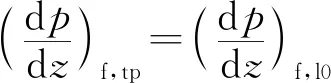
3.2 非均匀加热两相压降特性



4 结论

