弱胶结软岩巷道稳定性影响因素数值模拟研究

袁光明，张传朋

(1.重庆工程职业技术学院，重庆 402260；2.山东能源临矿集团菏泽煤电公司，山东 菏泽 274700)

0 引言

我国西部煤矿侏罗系地层居多，特点是岩体软弱，泥质胶结、遇水泥化、强度低[1]。而处在其中的软岩巷道极易出现大变形、大范围失稳破坏等一系列工程响应问题。为此大批专家学者展开了大量的研究并取得了较大的进展[2]。侯朝炯[3]基于经典的理想弹塑性理论分析了深部巷道围岩稳定性的影响因素，认为改善巷道围岩应力状态和围岩力学性能及提高支护阻力等是深部巷道围岩控制的有效途径。王卫军[4]等理论分析了深部高应力巷道围岩塑性区与支护阻力的关系，结论是塑性区半径对较小的支护阻力敏感性比较高，当支护阻力较大时，随着支护阻力的增大，敏感程度明显降低。赵志伟[5]等利用相似材料模拟试验得出巷道底鼓和顶板下沉现象除受预加高应力和连续载荷影响外，巷道的左右边墙破坏对巷道顶底板结构稳定性也有影响。芦德伟[6]基于采用水压致裂法对煤层地应力实测数据的分析，得出了巷道顶板稳定性受最大水平地应力的影响程度以及不同掘进方向巷道状况的差异。任杰[7]、张钊[8]理论分析了巷道围岩稳定性影响因素包括原岩应力、围岩性质、采动影响、支护结构属性等。陈曦[9]等采用正交数值模拟试验研究了岩体力学参数对隧道水平收敛、拱顶下沉量的影响。综上所述，目前针对弱胶结软岩巷道围岩稳定性影响因素与变形破坏的直接关系的研究还不多见。鉴于此，本文以宁夏榆树井煤矿11801工作面顺槽为工程背景，利用直观形象的数值模拟方法，探寻岩体力学性质、地应力、支护阻力等影响围岩稳定性的因素与巷道四周变形破坏的直接关系。

1 建立数值模型

11801工作面顺槽巷宽4.2 m，高3.0 m，为矩形巷道，设计长度为950m(如图1所示)。工作面开采煤田8#煤层，厚度大且较稳定，平均厚度2.52 m，属中含煤组上部第三含煤段中部煤层，局部含1层粉砂岩或细砂岩夹矸，煤层倾角大致为8°。8#煤层顶板为粉砂岩，深灰黑色，粉砂质结构，泥质胶结，含炭屑，煤屑、植物化石及黄铁矿结核，厚度15.12 m；底板也为粉砂岩，浅灰色，分选较好，局部波状层理发育，泥质胶结，含少量炭屑，厚度5.12 m(如图2所示)。基于莫尔-库仑屈服准则，运用FLAC3D建立数值模型，如图1所示。模型坐标系原点设在巷道顶板中点，巷道轴向设为Y方向，水平面内与Y垂直的方向设为X方向，与水平面垂直的方向即为Z向。模型Y方向取5 m，另两个方向均取30 m。为更精确地研究巷道围岩的位移场分布规律，模型基准单元大小为0.75 m，并以1.05的比率向外扩展，由此得模型共16000个单元，17491个节点。模拟所用岩体原始参数见表1，水平应力值为17.15 MPa，垂直应力值为8.35 MPa，所有参数均为该矿地质分析报告所提供。

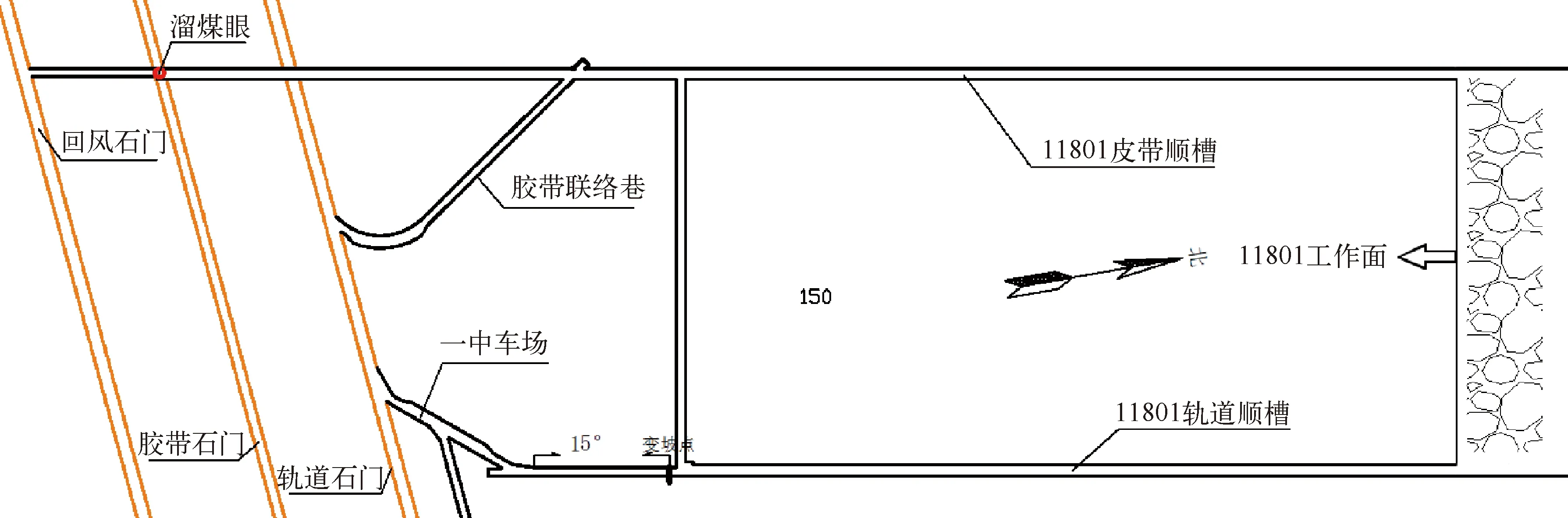
图1 工作面位置及顺槽位置示意图

图2 煤层顶底板综合柱状图

图3 数值计算几何模型

表1 各岩层物理力学参数

2 岩性与围岩稳定性的关系

围岩物理力学性能(弹性模量、粘聚力、内摩擦角等)是影响巷道围岩稳定性的主要因素，著名学者Kastener已经给出了数学表达式[3]。为探究这些因素与弱胶结软岩巷道围岩顶底板、两帮变形的具体关系，依次采用成比例改变其中一个因素，固定另两个因素的方式开展数值模拟。

2.1 弹性模量对巷道稳定性的影响

基于岩体原始参数(见表1)作为一个模拟方案2，然后将弹性模量分别减小1倍，增大2倍、4倍作为模拟方案1，3，4(见表2)。模拟结果见图4 和图5。

表2 弹性模量变化表

图4 不同方案x和z方向位移云图

图5 不同弹性模量条件下巷道表面围岩最大位移比较图

由图4和5可以看出随着弹性模量的逐渐增加，巷道表面位移均单调递减。方案1中，巷道围岩左右帮的位移分别为477.8 mm和477.3 mm，顶底板位移分别为939.4 mm和655.8 mm。而方案4中，巷道围岩左右帮的位移分别为59.72 mm和59.66 mm，分别都减小了8倍，顶底板位移分别为117.4 mm和81.98 mm，也分别减小了8倍。可见，随着弹性模量增加，巷道围岩变形量显著减小。有研究表明沉积岩石的弹性模量均随围压增大而增大[10]，而围压等价于支护体的支护阻力，因此，为增强巷道围岩整体性和稳定性，应尽量提高支护阻力；也可发现，随着弹性模量逐渐增大，巷道围岩变形速率呈现先快后慢的规律。例如弹性模量从方案1变化到方案2时左帮最大位移变化了469.7 mm，而从方案3变化到方案4时左帮最大位移仅变化了117.4 mm。由图表推测可知当弹性模量再增大时巷道围岩位移变化将保持较低的变形速率；4个方案中巷道围岩变形规律一致，具体为顶板下沉量最大，底板臌起量次之，顶底板的收敛量大于两帮收敛量。以方案3为例，巷道顶板下沉量234.8 mm是底板臌起量164 mm的1.43倍。顶底收敛量398.8 mm是两帮收敛量238.7 mm的1.67倍。总之，巷道围岩变形都是顶板下沉量最大，底板鼓起量次之，两帮变形量最小。

2.2 粘聚力对巷道稳定性的影响

基于岩体原始参数(见表1)作为模拟方案6，然后将粘聚力分别减小1倍，增大2倍、4倍作为模拟方案5，7，8(见表3)。模拟结果见图6和图7。

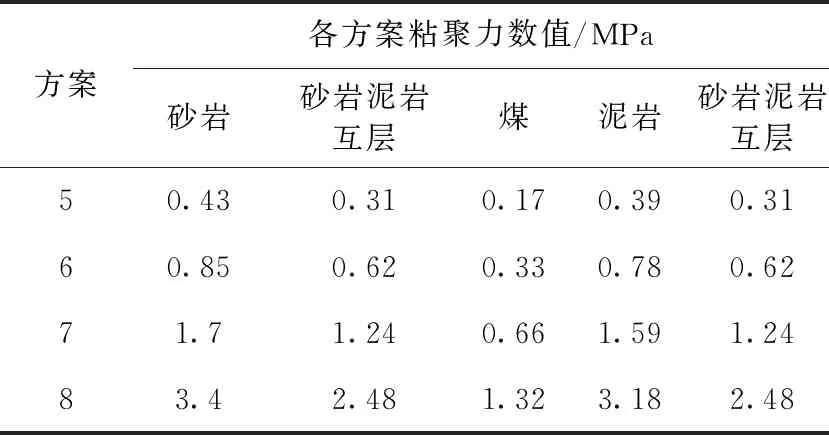
表3 粘聚力变化表

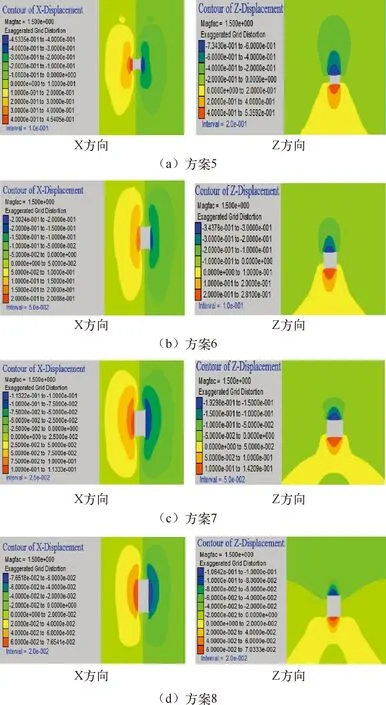
图6 不同方案x和z方向位移云图

图7 不同粘聚力条件下巷道表面围岩最大位移比较图

由图6和图7可以看出随着粘聚力的逐渐增加，巷道表面位移均单调递减。粘聚力在方案5时，巷道围岩左右帮的位移分别为463.8 mm和464.5 mm，顶底板位移分别为734.4 mm和535.6 mm。而粘聚力在方案8时，巷道围岩左右帮的位移分别为77.9 mm和77.94 mm，分别都减小了6倍，顶底板位移分别为106.4 mm和70.31 mm，分别减小了6.9倍和7.6倍，可见，随着粘聚力增加，巷道围岩变形量显著减小。因此，应优先选择锚杆、注浆等能有效提高锚固区围岩粘聚力的支护方式；也可发现，随着粘聚力的逐渐增大，巷道围岩变形递减速率呈现先快后慢的规律。例如粘聚力从方案5变化到方案6时左帮最大位移变化了261.6 mm，而从方案7变化到方案8时左帮最大位移仅变化了35.76 mm。由图表推测可知当粘聚力再增大时巷道围岩位移变化将保持较低的变形速率；4个方案中巷道围岩变形也均呈现出不对称，具体与弹性模量变化引起的变化规律一致。如以方案6为例，巷道顶板下沉量343.8 mm，是底板臌起量280.9 mm的1.22倍，顶底收敛量624.7 mm，是两帮收敛量403.9 mm的1.55倍。但是当粘聚力在增大到一定数值以后，底板鼓起量将小于两帮变形量。

2.3 内摩擦角对巷道稳定性的影响

基于岩体原始参数(见表1)作为模拟方案10，然后将粘聚力分别减小1倍，增大2倍、4倍作为模拟方案9，11，12(见表4)。模拟结果如图8 和图9所示。

表4 内摩擦角变化表

续表

图9 不同内摩擦角条件下巷道表面围岩最大位移比较图

由图8和图9可以看出随着内摩擦角的逐渐增加，巷道表面位移也均是单调递减，但减小量较小。在方案9中，顶底板位移分别为129.1 mm和84.98 mm，而在方案12中，顶底板位移分别为75.82 mm和53.61 mm，分别只减小了1.7倍和1.6倍。尤其是两帮的变形减小量更小，近乎一条水平线。如在方案9中，巷道围岩左右帮的位移分别为85.29 mm和85.19 mm，而在方案12中，巷道围岩左右帮的位移分别为69.76 mm和69.74 mm，分别仅减小了15.53 mm和15.45 mm。可见内摩擦角的变化对两帮变形的影响很小，因此，内摩擦角的变化主要对巷道顶板和底板产生影响；也可发现，不同内摩擦角条件下巷道围岩变形不对称的特点表现不明显。以方案12为例，巷道顶板下沉量75.82 mm，仅比底板臌起量大22.21 mm，两帮收敛量139.5 mm，仅是顶底板收敛量129.43 mm的1.08倍，变形量相近。

3 地应力对巷道稳定性的影响

地应力组成因素很多，岩体的变形破坏与所处的应力环境密切相关，它的大小是巷道围岩产生大变形与破坏失稳的主要影响因素[4,11，12]。为详细分析地应力对弱胶结软岩巷道围岩稳定性的影响，通过控制侧压系数不变，改变垂直应力值和控制垂直应力值不变，改变侧压系数两种情况来模拟巷道围岩的位移变化规律。

3.1 垂直应力对稳定的影响

控制原岩侧压系数λ=17.15/8.5≈2，分别取垂直应力为4 MPa、6 MPa、8 MPa和10 MPa 4种情况模拟应力应变变化规律，结果见图10和图11。

图10 不同垂直应力时x和z方向位移云图

图11 不同垂直应力条件下巷道表面围岩最大位移比较图

由图10和图11可知，垂直应力与巷道围岩变形基本呈现正比例关系，随着垂直应力的增大，巷道变形线性增加。随着垂直应力的增大，巷道顶底板和两帮变形图还呈现出一个共同的特点：图线斜率先小后大再变小，如当垂直应力从4 MPa 增加到4 MPa时图线斜率小于垂直应力从6 MPa增加到8 MPa时的斜率，而垂直应力从8 MPa增加到10 MPa时图线斜率也小于垂直应力从6 MPa增加到8 MPa时的斜率。由此可知，随着垂直应力的增大，巷道变形速率表现出先小后大再变小的规律；垂直应力对巷道顶板下沉量的影响最大，例如垂直应力为4 MPa时，顶板下沉量为114.6 mm，而底板鼓起量为69.89 mm，左右两帮分别为58.51 mm 和58.62 mm，顶板下沉量是底板鼓起量的1.64倍，是两帮位移量的1.95倍。当垂直应力为8 MPa时，顶板下沉量为453.8 mm，而底板鼓起量为311.3 mm，左右两帮分别为230.10 mm 和229.71 mm，顶板下沉量是底板鼓起量的1.46倍，是两帮位移量的1.97倍。可见，巷道设计和支护时应充分考虑垂直应力对顶板下沉量的影响。

3.2 测压系数对稳定的影响

保持垂直应力为8 MPa不变，设置侧压系数以0.1的增加幅度从0.4一直增加到2.0，模拟17个侧压系数情况下巷道围岩变形状态。

由图12可知，巷道围岩变形与侧压系数的大小也均呈正比例相关关系，随着侧压系数的增大，巷道顶底板和两帮变形均线性增加。整个过程巷道顶板变形量和增加幅度始终最大，如λ为0.4时，顶板下沉量为156.37 mm，底板下沉量为58.77 mm，左右两帮分别为102.74 mm和100.87 mm。λ为2.0时，顶板下沉量为417.11 mm，底板下沉量为288.14 mm，左右两帮分别为210.52 mm 和208.97 mm。顶底板和两帮位移量增加幅度依次为261.40 mm，229.37 mm，107.78 mm和108.10 mm，这说明侧压系数对顶板位移的影响最大。也可发现，在λ为1.1的位置，底板和两帮的变形图线出现了交叉，在交叉之前(λ≤1.1)时左右两帮位移量大于底板的鼓起量，交叉之后(λ>1.1)底板的鼓起量大于两帮的位移量。由此说明，底板的变形对侧压系数的改变相比两帮更为敏感。由此也印证了有的学者关于水平应力是引起软岩巷道底鼓的主要因素的观点。

图12 围岩变形与侧压系数的关系

4 支护阻力对巷道稳定性的影响

通常情况下，较大的支护阻力对减小围岩变形是有利的，因为支护阻力可以抑制破碎的岩体张开和滑动，巷道围岩的整体性和稳定性从而得到保证[2,13,14]。为详细分析支护阻力与弱胶结软岩巷道四周变形的具体关系，模拟支护阻力分别为0 MPa、0.2 MPa、0.3 MPa、0.4 MPa、0.5 MPa、0.6 MPa 六种方案下巷道围岩变形规律。

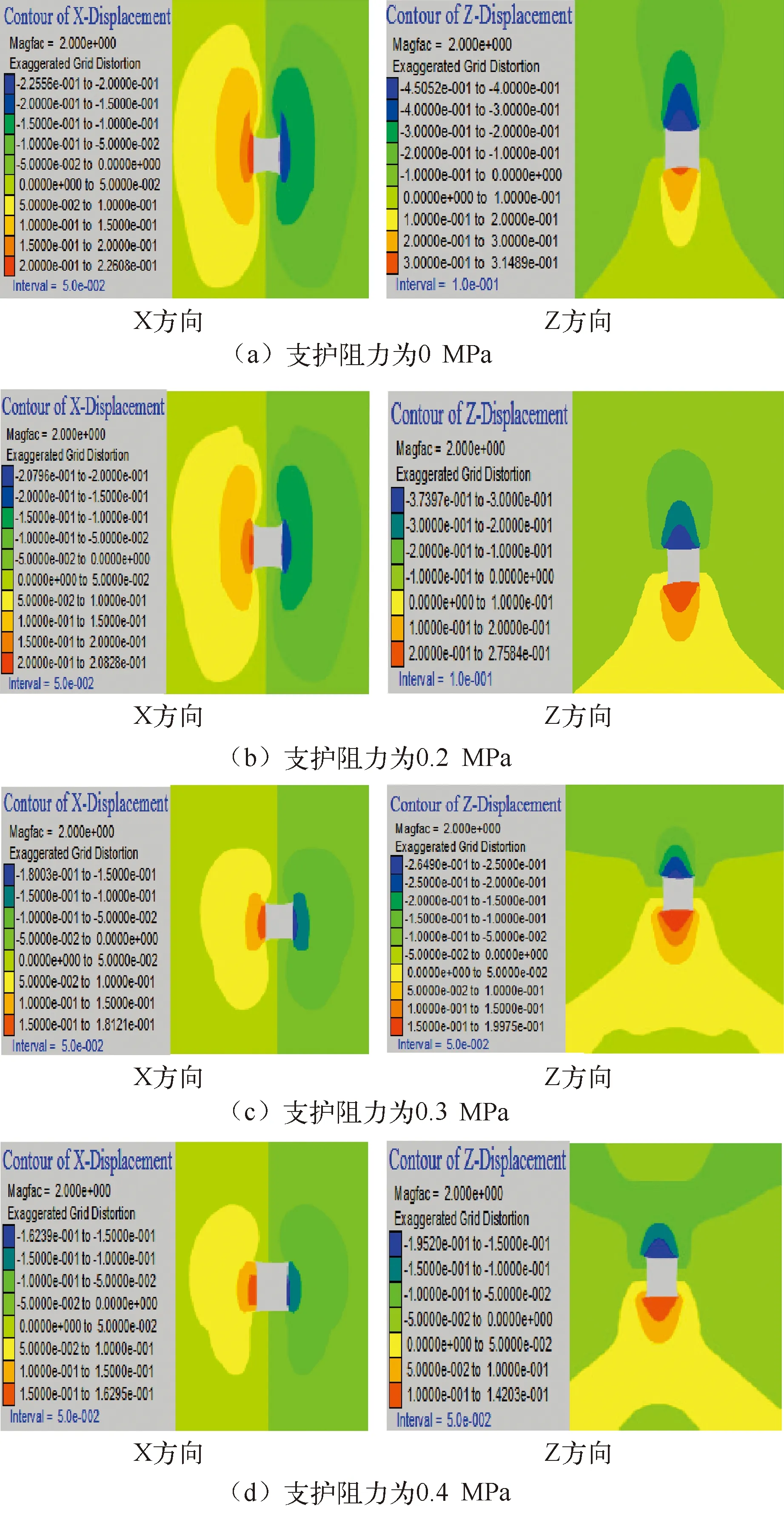
图13 不同支护阻力时x和z方向位移云图

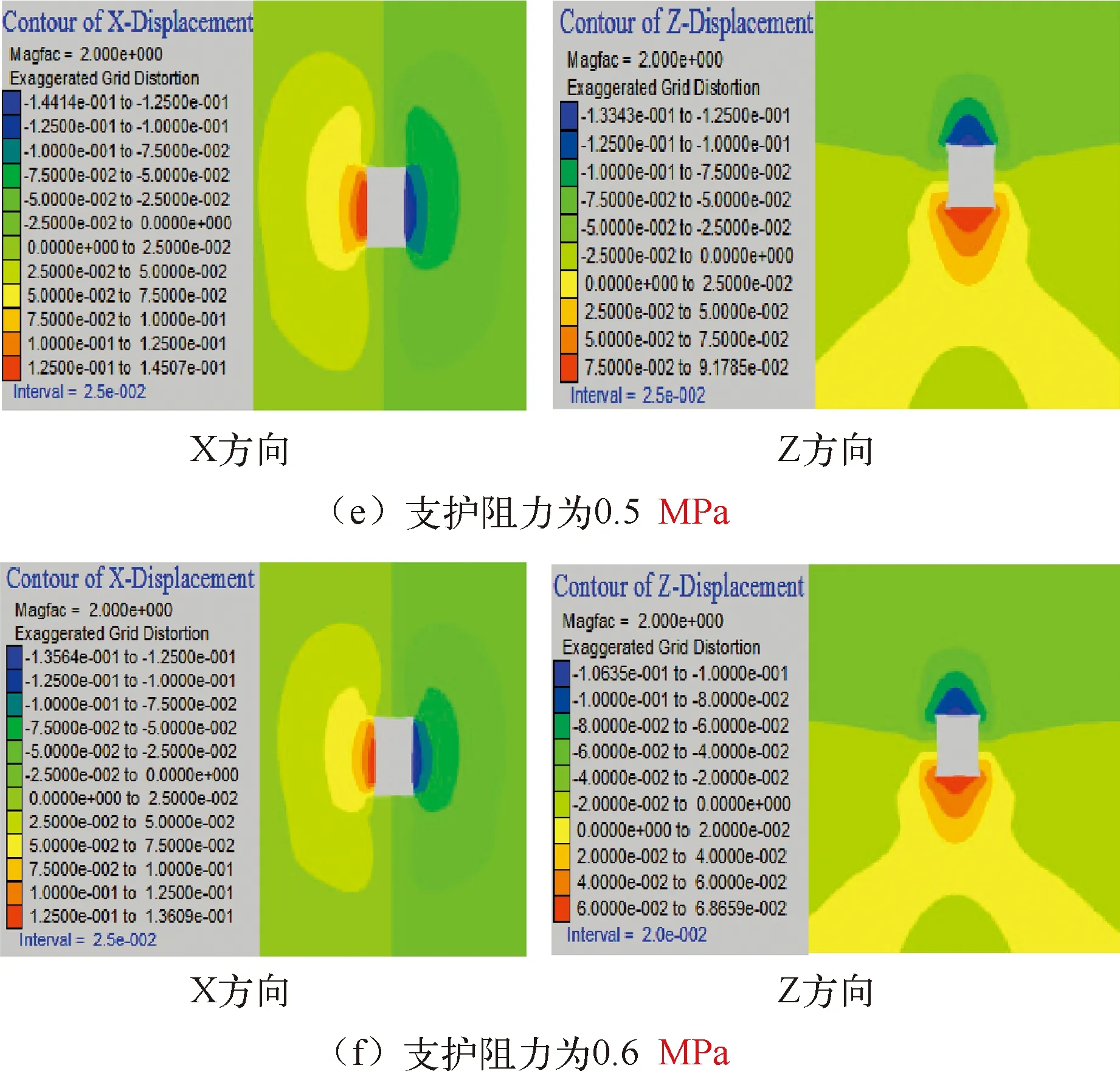
图13 不同支护阻力时x和z方向位移云图(续)

由图14可知支护阻力对巷道围岩变形影响较大，随着支护阻力的增大巷道四周变形均在单调递减。例如支护阻力为0.2 MPa时，顶板下沉量为377.12 mm，底板鼓起量为280.27 mm，左右两帮位移量分别为207.15 mm和205.77 mm，而支护阻力增大到0.5 MPa时顶板下沉量降到了140.55 mm，底板鼓起量则降到了91.77 mm，左右两帮也降到了147.24 mm和148.56 mm，顶底板和左右两帮变形减小量分别达236.57 mm，188.50 mm，59.91 mm和57.21 mm。巷道四周变形还表现出一个共同规律：根据位移减小幅度可将整个过程分为三个阶段，支护阻力较小时(00.5 MPa)，随着支护阻力的增大，巷道四周变形递减速率又开始降低。如支护阻力为0.5 MPa时底板位移为91.77 mm，已经控制在了100 mm范围内。支护阻力为0.6 MPa时底板位移为74.71 mm，相比0.5 MPa的阻力仅减小了17.06 mm。由此可知，在考虑支护方案时不能一味寻求提高支护阻力，而是应要求在持续提供较高支护阻力前提下，支护结构还具有一定的连续变形能力，以容纳围岩部分“给定变形”。这里的74.71 mm可以认为是巷道围岩控制时所应考虑的底板“给定变形”量；也可发现，左右两帮的位移曲线与顶底板的位移曲线在图中一些位置出现了交叉，从总体上看左右两帮的位移曲线相对变化比较平稳，顶底板的位移曲线相对比较陡峭，此说明支护阻力对抑制巷道顶底板位移的能力强于抑制左右两帮收敛变形的能力。

图14 不同支护阻力时表面围岩最大位移比较图

5 结论

(1) 弹性模量和粘聚力的变化对巷道围岩变形量的改变有显著的影响，内摩擦角的变化对巷道围岩变形量的改变也有一定的影响，但是影响程度与前两者相比较小。一定范围内，弹性模量和粘聚力的变化对巷道顶底板收敛量的影响大于对两帮收敛量的影响，而内摩擦角的变化巷道围岩变形不对称的特点不明显。

(2) 地应力越大，围岩稳定性越差。垂直应力和测压系数的改变对顶底板围岩位移量的影响较大，对两帮的影响相对较小。但随着侧压系数的增大，围岩顶底板和两帮变形均呈单调递增的趋势，说明水平应力对巷道变形破坏的影响更为突出。

(3) 支护阻力越大，围岩稳定性越好。支护阻力较小时，支护阻力的提高可以迅速减小围岩的变形量，尤其是顶底板的位移量。当支护阻力超过0.5 MPa时，围岩位移量变化幅度大大减小，最佳的支护方案是支护结构既具有持续较高的支护阻力又有一定的连续变形能力，以允许围岩一定的变形。