空间机械臂关节电流环预测控制研究*

唐艺伟，吕振华，孙 欣，肖 曦，张 猛

0 引 言

空间在轨服务任务(on-orbit servicing，OOS)包括设备组装、燃料加注、维修升级等，是节约空间设备在轨运行成本的重要手段，而空间机械臂技术是执行在轨服务任务最有前景的方向[1].机械臂关节是空间机械臂的核心部件，起着机械连接、位置感知、产生与传递动力三种作用，是影响机械臂运动精度、跟踪速度以及工作安全性等系列指标的关键因素.

空间机械臂关节大多采用电气驱动，以基于坐标变换的电流解耦控制为核心，在此基础上实现转速控制及位置控制，其整体结构通常呈现多控制环嵌套式，如图1所示.图中，ω为电机转速，id,iq为电机d/q轴电流，ia,ib为电机a相和b相电流，ud,uq为电机d/q轴电压，上标“*”表示各物理量目标值.电流环是多控制环嵌套结构的最内层，其主要性能指标是动态响应速度，在频域表示下即为闭环系统带宽.动态响应快、超调量小、且具有一定参数鲁棒性的电流环是高性能伺服系统的必要条件.传统PI控制器简单可靠，广泛运用于各种工业场合，然而难以兼顾响应速度和超调量.

上世纪70年代中后期以来，预测控制在多个工业过程控制领域得到了成功应用.在预测控制中，控制器不只利用已有的状态量和控制量信息，而且基于被控对象的数学模型对系统未来一段时间的状态作出预测.近年来，有不少学者对预测控制在电力传动领域的应用开展了研究[2-5].其中，预测控制方法应用于永磁同步电机与逆变器系统中，可实现对电机电流的高精度控制，进而提升伺服系统的整体性能.MOREL等[6]将电流预测控制分为3类：直接预测控制(direct predictive control, DPC)、双矢量预测控制(two-configuration Predictive control, 2PC) 和PWM预测控制(PWM Predictive control, PPC)，其中PWM预测控制也被称为无差拍控制，是指让离散系统的输出在最少的周期内进入稳态的一类控制方法.对于常规的电流环数字实现方案而言，输出最快可在两周期达到稳定，这是电流环动态响应的理论上限.利用永磁同步电机和逆变器系统离散数学模型，借助无差拍控制思想，可以直接计算得到使电流在两周期内跟踪目标值的参考电压.这种算法思路自然、结构简单，控制效果优于传统PI调节器，但严重依赖于被控对象的精确数学模型.对此很多学者进行了深入研究，提出各种改进算法[7-11].文献[7]中削弱无差拍控制的约束条件，降低了电流偏差项的权值，同时采用电压的平滑预测值，相比传统预测控制方法增强了系统鲁棒性，但其电流响应则变缓.文献[8]通过在d轴电压指令中加入误差积分项消除由于模型参数不匹配造成的d轴电流静差，同时利用磁链的动态调整间接消除q轴电流静差，提升了在参数失配时的系统鲁棒性.文献[9]使用在线参数辨识方法对电感电阻等参数进行实时校正，消除了不准确的参数对预测控制效果的影响.文献[10]引入权重因子，采用一种改进的无差拍鲁棒电流控制结构，并提出了转子角度的补偿方法，但同时也在一定程度上降低了动态性能.文献[11]引入龙伯格观测器，提出了一种鲁棒电流预测控制算法，可以通过鲁棒性系数的调节提高系统相角裕量从而提升系统的稳定性，但该方法同样以牺牲系统带宽为代价.

传统的无差拍预测控制本质上采用的是开环控制结构，对模型参数依赖明显，在参数不准确时容易产生电流静差.本文在传统的一阶无差拍电流预测控制的基础上，提出一种高阶无差拍电流预测控制策略，此种策略可使电流环动态响应速度逼近理论上限，同时结构简单、便于数字实现、具有一定参数适应能力.相比PI调节器，系统进入稳态的响应时间明显缩短，系统带宽得到极大提升；相比传统的无差拍预测控制，高阶无差拍方法对于电机电阻与磁链参数变化具有更强的适应性，在参数失配的条件下具有更好的动态与稳态性能.

图1 永磁同步电机磁场定向控制系统框图Fig.1 Diagram of PMSM FOC system

1 永磁同步电机电流环离散模型

在永磁同步电机的实际应用中，常使用电压型PWM逆变器驱动.在此种场合下，电流环是一个典型的混杂系统，电枢模型为其连续部分，PWM逆变器模型为其离散部分.通常，控制周期和PWM周期等长，在每个控制周期开始时，控制器对电机物理量进行数值采样，并依据控制律计算得到控制输出，在下个控制周期开始时更新控制输出.

现有对永磁同步电机磁场定向控制的研究大多基于如式(1)所示的经典理想模型：

(1)

式中，R为电枢电阻，Ld,Lq为电机d/q轴电感，ψd为永磁体d轴磁链，Tem为电机输出的电磁转矩，其余符号意义同前.伺服控制领域里，常选择d轴电流目标值为0，而q轴电流目标值由转速环控制器给出；转速目标值则由外界直接给定或由位置环控制器给出.考虑到d轴电流环的动态性能对伺服系统整体影响不大，可以采用传统的PI控制器，以下仅考虑q轴电流环的设计.改写式(1)中的q轴电压方程并解得：

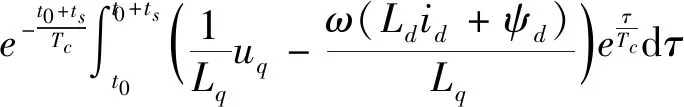
(2)

其中t0,ts分别代表起止时间，Tc=LqR，为q轴电流环的时间常数.

记iq[n]=iq(nT)为第n个控制周期开始时的q轴电流值，其中n为整数，T为控制周期，方括号表示离散量，圆括号表示连续量.在式(2)中取t0=nT,ts=T，可得

(3)

记uq[n]为控制器在获得iq[n]信息后，依据控制律计算得到的q轴电压输出.忽略逆变器的SVPWM实现细节及死区效应，由前述的控制时序可知：

uq(τ)=uq[n-1],nT≤τ<(n+1)T

(4)

从而有

(5)

(6)

将式(5)、(6)代入式(4)，同时令

(7)

可得

iq[n+1]=αiq[n]+β(uq[n-1]-q[n+1]

(8)

频域表示为

(z-α)Iq(z)=βz-1Uq(z)-βzEq(z)

(9)

此即q轴电流环的离散模型.

2 一阶形式无差拍预测控制器

2.1 一阶无差拍预测控制器

按作用不同将式(8)中的q轴电压分解为两部分，即

uq[n-1]=uq1[n-1]+uq2[n-1]

(10)

其中uq1用作调节电流，由q轴电流环控制策略给出；uq2用作抵消反电动势，由q轴电流环补偿策略给出.

首先假设补偿完全精确，讨论控制策略的设计，为此令

uq2[n]=q[n+2]

(11)

后文将讨论补偿策略的设计及不精确补偿的影响，并针对此问题发展高阶形式无差拍控制器.

(12)

式(12)中含有iq[n+1]，这是第n+1个控制周期开始时的测量值，在第n个控制周期开始时尚不可知，但通过式(8)可以进行预测：

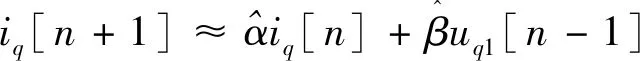
(13)

式(13)右侧各物理量在第n个控制周期开始时已知.

将式(13)代入式(12)可得

(14)

频域表示为

(15)

容易得到闭环系统传递函数如下：

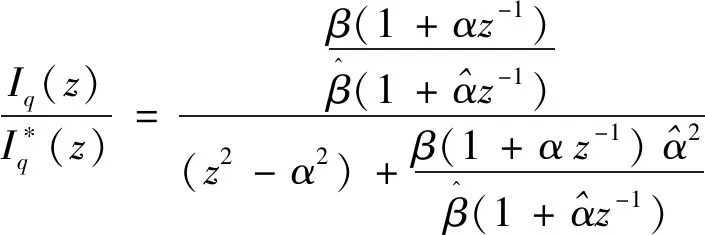
(16)

(17)

即q轴电流环对阶跃电流指令的响应存在稳态误差，这在实际系统中是难以接受的.

2.2 并联积分器的一阶无差拍预测控制器

2.1节指出当控制器存在参数误差时，即使反电动势的影响被精确补偿，一阶无差拍预测控制器仍然无法消除q轴电流阶跃响应稳态误差，对此一个自然的改进方法是在控制器两端并联积分器，如图2所示.由于控制周期内反电动势相对于q轴电流变化缓慢，其影响效果也近似体现为阶跃响应下产生稳态误差，因而使用积分器有望抵消反电动势影响，不必要额外对反电动势进行补偿.

图2 并联积分器的一阶无差拍预测控制器示意Fig.2 Diagram of first order deadbeat predictive controller with parallel integrator

取

(18)

其中f(z)/(z-1)为积分器的传递函数，f(z)=1和f(z)=z分别对应于前向欧拉积分和后向欧拉积分.

(19)

(20)

容易发现，由于f(1)≠0，

(21)

即q轴电流环对阶跃电流指令的响应不存在稳态误差，即使存在常数反电动势或者参数误差也不改变此结论.一般而言，Iq(z)/Eq(z)呈现高通特性，调整f(z)可以改变Iq(z)/Eq(z)的极点，进而改变q轴电流环对反电动势的抑制性能.

3 高阶形式无差拍预测控制器

基于2.2小节的分析，容易得到一阶无差拍预测控制器的高阶推广.类似于并联积分器，使用高阶形式控制器最主要的动机是消除低频反电动势的影响.

(22)

在式(22)等号左右两侧分别差分，可得

(23)

频域表示为

(24)

(25)

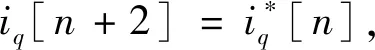
(26)

选择N=2作为算例进行说明.为消除等号两侧同乘(1+η1z-1+η2z-2)后的zIq(z)项，令

(27)

(28)

从而得到控制律

(29)

时域形式为：

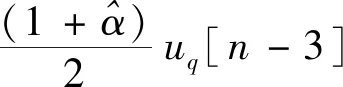
(30)

4 仿真验证

使用MATLAB/Simulink对式(30)给出的控制律进行仿真验证，仿真算例的参数如表1所示.定子绕组每相电阻、d/q轴电感、d轴磁链参数来自于科尔摩根型号为TBMS-12941-A的无框永磁同步电机；PWM周期为100 μs，对应于开关频率10 kHz.

首先使用传统PI控制器对d轴电流环和q轴电流环进行控制，其频域表示为

(31)

通过多次数值实验，选取控制效果较好的一组参数kp=2.6,ki=700作为控制器效果对照.

表1 电流环高阶无差拍预测控制器仿真参数Tab.1 Simulation parameters of high-order deadbeat predictive controller for current loop

可以看出，使用PI控制器时，闭环系统对q轴电流目标值的正弦稳态响应既有相位滞后、又有幅值衰减，而使用无差拍预测控制器时仅有两拍的滞后；使用PI控制器时，闭环系统大约经过6 ms进入稳态，而使用预测控制器时仅需两倍控制周期，即200 μs.综上，无差拍预测控制器相对于传统的PI控制器具备更高的动态响应速度和更高的带宽.

图3 传统PI控制器与无差拍预测控制器电流环伺服控制效果对比Fig.3 Comparison of current loop servo performance between conventional PI controller and deadbeat predictive controller

以下基于仿真算例考虑控制器参数误差的影响.由式(29)和式(9)可得闭环系统的特征方程

(32)

(33)

(34)

图4给出了闭环系统随γ的根轨迹.由图中可以看出，当电感参数的相对误差不超过20%时，闭环系统的极点均有较小的幅值，此时q轴电流环仍有较好的动态性能，即本文提出的无差拍预测控制器具有一定的电感参数适应能力.

图4 电流环不同电感参数误差下闭环系统根轨迹图Fig.4 Root locus of closed loop system under different inductance errors

选取和前文相同的仿真条件，分别令γ=-0.2,γ=0,γ=0.2，对控制效果进行比较，结果见于图5，可发现20%的电感误差对q轴电流环的性能无明显负面影响.

图5 电流环不同电感参数误差下闭环系统伺服控制效果对比Fig.5 Comparison of closed loop system servo per for mance under different inductance errors

图6～8分别给出了磁链和电阻参数不准确时，高阶无差拍预测控制器与传统一阶无差拍预测控制器的性能比较.考虑闭环系统的电流阶跃响应，令q轴电流目标值在0.03 s时刻由0A跳变至1A，过程中保持电机转速不变.观察图6可以发现，当磁链参数出现50%的误差时，使用传统一阶预测控制器时，q轴电流阶跃响应存在稳态误差，而使用高阶预测控制器时不受影响.这是因为一阶预测控制器中，反电势补偿项因磁链误差而产生偏差，进而导致q轴电流出现稳态误差，而高阶预测控制器没有使用磁链项，因此阶跃响应不受磁链误差的影响.观察图7和8可以发现，当电阻参数出现50%的误差时，使用一阶预测控制器的闭环系统动态性能受影响的同时，q轴电流也出现了稳态误差，而使用高阶预测控制器可有效消除此稳态误差.因此，相比传统的一阶无差拍预测控制器，高阶无差拍预测控制器对于磁链与电阻参数变化具有更强的适应性.

图6 无差拍预测控制器磁链参数变化适应性Fig.6 Adaptability of deadbeat predictive controller under resistance variation

图7 无差拍预测控制器电阻参数变化适应性-总览Fig.7 Adaptability of deadbeat predictive controller under resistance variation

图8 无差拍预测控制器电阻参数变化适应性-细节Fig.8 Adaptability of deadbeat predictive controller under resistance variation

5 结 论

本文介绍了一种高动态响应的永磁同步电机无差拍电流预测控制方法.首先根据电流环的离散模型设计和分析了一阶无差拍预测控制器，在此基础上给出了高阶形式无差拍预测控制器的设计方法.仿真结果表明，与传统的PI控制器相比，本文提出的高阶形式无差拍预测控制器有效提高了电流环动态响应速度，将系统进入稳态响应的时间从6 ms降至200 μs.频域角度下，高阶形式无差拍预测控制器提升了闭环系统带宽，大幅减小了正弦响应的幅值误差.此外，无差拍预测控制器具备一定的参数鲁棒性，仿真算例表明高阶无差拍预测控制闭环系统能容忍达20%的电感参数误差.与传统一阶形式的无差拍控制器相比，高阶无差拍预测控制器对于电机电阻与磁链参数变化具有较好的适应性，可完全消除模型参数误差引起的q轴电流稳态误差.

应用本文提出的方法可使永磁同步电机电流环具有良好的动态和稳态性能，同时较好地适应电阻和磁链变化，作为伺服控制的基础有望在空间机械臂运动伺服系统中发挥重要作用.