打造以思维培养为导向的数学课堂——以人教版《数学》五年级下册“探索图形”教学为例

洪菲菲

（福建省厦门实验小学集美分校）

数学是思维的体操。在数学教学中，学生思维的参与是学习效果的前提和保证，其思维能力的培养是数学教学的重要目标。数学教学不仅要重视知识技能的习得，更要重视学生思维的激活、引导和提升。下面以人教版《义务教育教科书·数学》五年级下册“探索图形”一课为例，谈谈以思维培养为导向的数学课堂教学如何为学生的思维而教，为提升学生的数学素养而教。

一、驱动——点燃思维“火花”

学生与生俱来就带着“灵气”。这种“灵气”，体现在他们对未知世界强烈的好奇心上，体现在他们对未知领域的挑战和探索上。好的数学课应当是灵活的，是闪烁着学生思维的火花的。数学教学中，教师要善于运用合适的问题和恰当的引导，将学生思维的“小火苗”烧得旺旺的，呈现出活泼的课堂样态。

在教学“探索图形”这节课时，我在课件上展示了边长为10厘米的大正方体，并开展了如下教学活动。

师：同学们请看，这个棱长为10厘米的大正方体是由多少个棱长为1厘米的小正方体拼成的？

生：10×10×10=1000。它是由1000个小正方体拼成的。

师：如果老师把这个大正方体的表面涂上颜色，这些小正方体会有几个面被涂上颜色呢？根据涂色情况把这些小正方体进行分类，你打算分为几类？先观察一下，再和同桌讨论。

生：可以分为四类。有三面涂色的，两面涂色的，一面涂色的和没有涂色的。

师：每一类小正方体各有多少个？请你们数一数，算一算。

生：太多了，太复杂了，算不清楚。

师：小正方体的数量太多，算起来不方便，怎么办？

生：可以从棱长小一些的正方体开始研究，看看是不是能找到规律。

师：你们建议从棱长是几厘米的正方体来研究呢？

生：从棱长是3厘米的正方体开始。

师：好，老师为你们提供了棱长为3厘米的正方体。请你们看一下活动要求。

课件出示：

（1）找出四类小正方体在大正方体中的位置；

（2）分类数出四类小正方体的块数；

（3）把想法和同桌交流讨论，把结果填入学习单中。

当学生沉浸于挑战某一个未知领域的乐趣中时，往往是其最富“灵气”的时刻。教师要善于创设情境，激发学生参与学习的欲望和热情。在本节课教学之初，我先抛出一个具有挑战性的问题——由1000个棱长为1厘米的小正方体所组成的大正方体在表面涂色之后，根据小正方体的涂色情况可以把它们分为几类，各有多少个？这样一个看似不难实则不易的问题，瞬间激起了学生继续探究的欲望。当学生自己提出从简单的情况入手研究时，也就寻找到了一种解决复杂问题的重要方法——化繁为简。这样的教学过程，比直接从棱长为3厘米的正方体入手研究，效果要好得多。原因在于学生总是喜欢挑战，享受征服未知领域的成就感。

学生的思维不仅要激活，也要引导。教师在教学中适时、适当的点拨，可以使学生的思维聚焦在重点处，思之有法，思之有益。如果不加引导，让学生直接数棱长为3厘米的正方体中四类小正方体的数量，学生可以较为轻松地数出来。但“随意地数”属于低层次思维，学生虽然数出了结果，却对探究后续问题没有明显益处。换而言之，学生要数，但要数得有思考，有方法。这里，需要教师及时点拨引导，凸显教师导的作用。在上述片段中，我在学生操作之前给出了活动提示——找出四类小正方体在大正方体中的位置，再数出每一类小正方体有多少个。这就要求学生在数小正方体数量的同时，必须关注每一类小正方体与大正方体点、棱、面之间的关系。学生明确了思考的方向，数小正方体的数量时就有了更多思维的参与，这样就数出了发现，数出了规律。

每个学生都带着天然的“灵气”，有时闪现，有时隐藏。教师既要充分激活学生的数学思维，让学生自然地投入到对问题的探究中去；又要做好学生的引路人，在适当的时机指明方向，点燃学生思维的“火花”，使得课堂更加灵动。

二、开放——拓展思维空间

大多数数学教师对死气沉沉的课堂都是反感的。很多教师时常抱怨学生脑子不活，思维跟不上自己的教学节奏。在看到这些课堂表象的同时，我们应当反思其背后的原因。要让学生的思维真正激活并且涌动起来，教师至少应当做好两件事情：一是设置精巧且具有思维价值的教学环节，二是营造轻松开放的课堂教学环境。教师应当重视教学情境的设计以及课堂氛围的营造，力求为学生提供更加开放的思维空间，使学生能够积极思考、踊跃发表、敢于批判。

学生在探究了棱长为3厘米的正方体之后，我为每个合作小组提供了棱长为4厘米的正方体，让学生数一数三面涂色、两面涂色、一面涂色和没有涂色的小正方体各有多少个。学生充分地观察讨论，在全班进行了汇报。

生：三面涂色的小正方体在大正方体的点上，有8个；两面涂色的小正方体在大正方体的棱上，每条棱上有2个，2×12，有24个；一面涂色的小正方体在大正方体的面的中间，每个面4个，4×6，有24个；没有涂色的小正方体在大正方体的内部，有4个。

生：三面涂色、两面涂色和一面涂色的小正方体的个数，我同意他的意见。但是没有涂色的小正方体，我认为是8个。

生：这个大正方体掰不开，看不到里面的情况。你们看（指着大正方体的上面，如图1），中间一面涂色的四个小正方体下面，不是藏着四个没有涂色的小正方体吗？

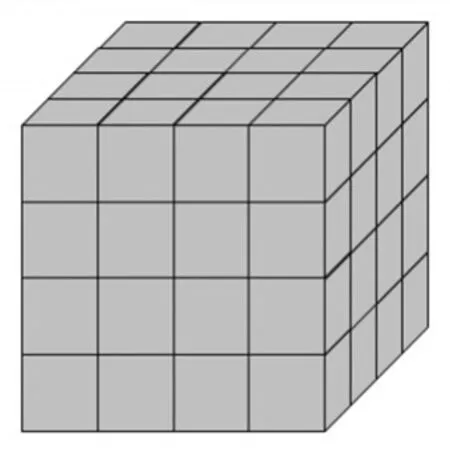
图1

生：你只看到了一层。去掉大正方体上面涂色的一层和下面涂色的一层，中间没有涂色的小正方体会有几层呢？所以应该是8个。

生：我用计算的方法来思考。小正方体的总数量是64个，去掉三面涂色的小正方体8个，两面涂色的24个，一面涂色的24个，64-8-24-24=8，没有涂色的小正方体应该有8个。

师：看得见的小正方体好数，看不见的小正方体难住了一些同学。到底是4个还是8个呢？

生：是8个。

师：让我们打开大正方体看看，是不是你们所想象的样子。（教师播放课件，如图2）

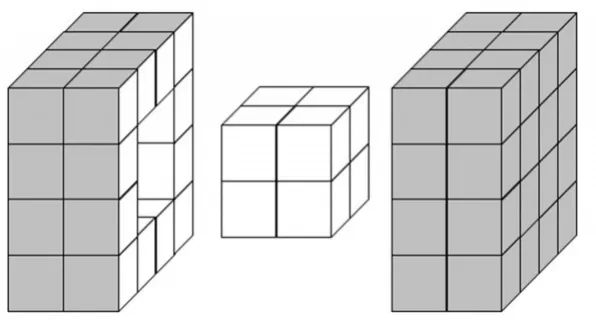
图2

数学教学应该努力为学生拓展思维空间，力图让学生的学习困惑暴露在外，并通过学生自身的“辨”及彼此间的“辩”，达到突破难点、提升思维的效果。数棱长为4厘米的正方体中三面涂色、两面涂色、一面涂色和没有涂色的小正方体的数量对学生而言具有一定的难度。一是要有序地数、找规律地数，才能数得清楚，数得有意义；二是没有涂色的小正方体包含在内，“看不见”的部分需要依靠学生的想象、推理才能数清楚。许多教师在教学本节课时，为学生提供了可拆分的大正方体，其目的就在于降低思维难度，使学生能够拆开看一看，一探究竟。本节课我反其道而行，提供的是不能拆开的大正方体。其目的就在于断了学生去“看”和去“数”的路子，而“逼”着学生去思考，去想象。一个小小的改变，为学生提供了思考和辨析的空间。

在上述教学片段中，空间想象和推理能力较弱的学生，在数没有涂色的小正方体数量时出现了困难，这正是学生思维困惑的真实体现。这个思维难点的暴露，成了学生“辩”的好时机。学生通过实物操作辅助想象，通过计算进行验证，多角度入手，在辨析中突破了这一难点。正是我在学具上动的“小手脚”，以及给予学生充分的时空和自由，学生的思维才得以充分激发，才使他们在思辨中培养了空间想象能力和推理能力。

三、抽象——提升思维品质

数学教学既要重视学生思维的激活与参与，更要重视将学生的思维引向深入，在深度思考中提升其思维品质。教学中，教师不能满足于学生学会解决一个问题，而要由一个问题引申开去解决一类问题。由“题”走向“类”的过程，是数学抽象的过程，也是学生数学思维提升的过程。

学生在探究棱长分别为3厘米、4厘米的大正方体中四类小正方体的数量时，已经感悟到了四类小正方体的数量与大正方体的点、棱、面之间的关系。即三面涂色的小正方体在大正方体的“点”上，两面涂色的小正方体在“棱”上，一面涂色的小正方体在“面”上，没有涂色的小正方体在“体”中间。即便发现了这样的关系，很多学生仍然停留在“数”和“算”的具体直观操作阶段。此时，教师应当引导学生继续深入探究，摆脱直观操作的局限，去寻觅其背后隐藏的数学奥秘。

（学生汇报棱长为4厘米的大正方体中四类小正方体的数量之后）

师：刚才汇报当中，我们得到了四类小正方体的数量。三面涂色的小正方体在大正方体的顶点上，有8个；两面涂色的小正方体在大正方体的棱上，有2×12=24个；一面涂色的小正方体在大正方体的面上，有2×2×6=24个；没有涂色的小正方体在大正方体中间，有2×2×2=8个。大正方体的棱长是4，为什么我们都用2来计算呢？这个2是怎么得来的？它和棱长4有什么关系吗？

生：两面涂色的小正方体在大正方体的棱上，一条棱上有4个小正方体，去掉头和尾的两个三面涂色的小正方体，剩下2个两面涂色的小正方体。所以，用（4-2）×12=24个。

生：一面涂色的小正方体在大正方体每一面的中间，每一面去掉上下两行和左右两列，用（4-2）²算出一个面有4个，再乘6个面，得到24个小正方体。

生：没有涂色的小正方体在大正方体的内部。去掉外面涂色的一层，用（4-2）³算出有8个。

师：如果计算棱长更大一些的正方体，你们有信心吗？没有学具让你们操作了，你们还能算得出来吗？

生：能。（合作小组计算棱长分别为5厘米、10厘米的大正方体中四类小正方体的数量）

师：这样算下去，算得完吗？如果棱长为n，你们能写出每一类小正方体的数量吗？

生：三面涂色的有8个，两面涂色的有（n-2）×12个，一面涂色的有（n-2）²×6个，没有涂色的小正方体有（n-2）³个。

师：总结得太棒了！你们找到了这个规律，就能解决这一类问题。请你们再思考一下，这个n可以是任意自然数吗？

生：不可以，n≥2。

学生在前面的操作中，发现了四类小正方体与大正方体点、面、棱之间的关系，品尝到了自主探究发现的美妙“滋味”。这时，教师应该趁热打铁，继续带着学生向知识的更深处探寻。

在上述教学中，我先引导学生思考一个关键问题：为什么棱长为4厘米，而我们都用“2”来计算呢？通过对这个问题的思考，使学生将关注点从计算转移到算式中的“2”与棱长的关系上来。在对这个问题的思考和讨论中，计算模型逐渐“浮出水面”。这时，我提出新的要求，不再提供学具，让学生计算出棱长分别为5厘米、10厘米乃至n厘米的大正方体中四类小正方体的数量。学生有了前面思考的基础，抽象出计算公式也就变得水到渠成。公式的提炼，使得学生掌握了解决这一类题目的“通法”。提炼公式的过程，使得学生的思维得到了锻炼，思维品质得到了显著提升。

好的数学课，因为有了学生思维的积极参与而变得生动有趣，因为有了学生思维的发展提升而显得更有价值。数学教学应当着力于增加学生的思维活跃度，开拓其思维空间，提升其思维品质。数学教学应当为学生的思维而教，为提升学生数学素养而教。