基于CEEMD小波包算法的降噪方法研究

孙晓娟,王 利

(宝鸡文理学院电子电气工程学院,陕西 宝鸡 721013)

0 引 言

脑电信号(Electroencephalograph, EEG)是一种能够揭示大脑活动状态的生物电信号。人体的许多生理与病理信息都能通过脑电信号反映出来[1]，因而脑电信号在大脑功能的开发与临床疾病的诊断等方面应用非常广泛[2]。但是，由于脑电信号具有十分微弱的特性，在采集时很容易受到噪声的干扰，从而对后续脑电信号的信息提取与特征分析产生极大的影响，因此对脑电信号进行降噪已经成为脑电信号分析中不可或缺的组成部分。

目前，EEG的降噪方法主要包括独立分量分析(Independent Component Analysis, ICA)[3-4]、小波变换(Wavelet Transform, WT)[5-7]和经验模态分解(Empirical Mode Decomposition, EMD)[8-9]。独立分量分析可以把脑电信号中的理想信号与噪声作为独立成分进行分离，从而实现降噪，但是仅适用于脑电信号通道数大于所分离的信号源数的情况[10-11]。小波变换则是通过先将脑电信号进行多尺度分解，然后对得到的小波系数进行处理来完成降噪的过程，但是这种方法的计算量较大，且小波基的选择需要大量的先验知识[12-13]。而经验模态分解方法不受上述问题的限制，它只需结合信号的特性，将脑电信号自适应地分解成多个固有模态函数(Intrinsic Mode Function, IMF)分量，从中选出部分IMF分量进行去除或者阈值处理，再进行信号重构就可以获取降噪后的脑电信号[8,14-15]。然而在使用过程中，EMD方法会出现模态混叠的现象[16-17]，为了解决此类问题，文献[18]提出了集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)，通过添加白噪声来修正EMD的模态混叠问题。随后，文献[19]又提出了完全集合经验模态分解(Complete Ensemble Empirical Mode Decomposition, CEEMD)，进一步完善了EEMD方法的不足。文献[20]成功地将CEEMD方法应用于脑电信号的降噪中，但是它将脑电信号进行CEEMD分解后，仅选取近似熵最大的IMF分量作为降噪后的脑电信号，损失了一部分有用信息。文献[7]在2017年提出并应用小波变换的方法进行心电信号的去噪研究，文献[9]在2019年提出了以经验模态分解和极限学习机的脑电信号提取分类方法。综合以上各种去噪方法的利弊，本文在CEEMD分解的分频特性基础上[21]，结合小波包的优点，提出一种新的脑电信号的降噪方法——CEEMD小波包降噪法。首先利用CEEMD对含噪的脑电信号进行分解，然后用小波包阈值对含有部分噪声的IMF分量实施降噪，同时保留低频的IMF分量，最后将使用小波包阈值降噪的IMF分量和保留的IMF分量进行累加重构，从而得到最终降噪后的脑电信号。

1 基本理论

1.1 CEEMD算法

CEEMD方法的具体步骤如下：

将某原始信号记为x(t)，根据CEEMD理论，向其添加白噪声，白噪声记为ωi(t)，则原始信号变为x(t)+λ0ωi(t)，其中，噪音系数用λ0表示。使用经验模态分解方法对原始信号进行N次分解，按照EED方法可以得到第1个IMF分量:

(1)

分解后，其剩余的分量可以用以下方式表示：

r1(t)=x(t)-IMF1(t)

(2)

继续执行以上过程，将信号r1(t)+λ1E1(ωi(t))进行N次分解，第2次分解后的结果可以表示为：

(3)

将分解出的模态分量用Mi表示，则第j个剩余的分量可以表示为：

rj(t)=rj-1(t)-IMFj(t)

(4)

对于某次分解后的信号rj(t)+λjEj(ωi(t))，对其再次进行分解，可以得到j+1个分量，表示成如下形式：

(5)

重复执行以上过程，直至某次模态分量不可再分时，停止分解过程。可以得到J个分量，将最终的残差值记为：

(6)

公式(6)变形可得原始信号x(t)表达如下：

(7)

根据以上过程，CEEMD方法的基本过程就是对信号进行若干次模态分解，对其高频信号进行剔除或者降噪，然后再对剩余分量进行重构以得到最终的降噪后的信号信息，该方法较好地利用了EMD的优点，又能实现较好的去噪效果。

1.2 小波包去噪

1.2.1 去噪的阈值函数

在多分辨率分析信号时，高频段的信号分辨率较差，一般是对信号的频段进行指数等间隔划分，再在低频段部分做进一步的分解，这样做无法反映出损伤信息，很难表征信号的非平稳信息。小波包方法为信号分析提供更加精细的方法，在信号分析过程中对信号进行多层次划分，分别对低频带部分和高频带部分进行分解，而且可以自适应选择频段与信号频谱相对应。

在小波包去噪中，选择合适的阈值函数至关重要，在目前的阈值函数中，广泛应用的是硬阈值函数和软阈值函数。

硬阈值函数的表达式如式(8)所示，其中w表示小波系数，λ为给定阈值。

(8)

从式(8)中可以看出，硬阈值函数在-λ和λ处不连续，因此，重构信号在-λ和λ附近会出现振荡，不能达到原始信号的光滑性。

软阈值函数的表达式如式(9)所示，其中sgn(w)为符号函数。

(9)

从式(9)中可以看出，软阈值函数的连续性较好，但是软阈值函数的导数不连续，具有一定的局限性。

综合软、硬阈值函数的优缺点，构造如下阈值函数，其中k为调节因数。

(10)

1.2.2 阈值λ的选择

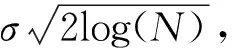
1.3 降噪效果的评价指标

在降噪效果上，一般有2个指标来进行评价，一个是信噪比(SNR)，另一个是均方根误差(RMSE)[22]。

SNR定义：

(11)

RMSE定义：

(12)

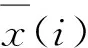
2 仿真信号分析

2.1 原始脑电信号和含噪声脑电信号仿真

本文采用MATLAB进行数据仿真，仿真过程如下：

1)建立脑电信号数学模型，脑电信号的模型相对复杂，但常用的模型在很多文献中已经提到，本文采用文献[23]中的脑电信号仿真模型来验证本文算法的降噪能力。原始的脑电信号仿真模型为：

(13)

2)选择合适的采样频率、采用点数。本文设计中选择采样频率f=250 Hz，采样点数为1001。

3)在信号s(t)中加入信噪比为2 dB的高斯白噪声，形成包含噪声的脑电信号。

4)编写MATLAB程序代码进行仿真，仿真结果如图1所示，图1包含了原始脑电信号和含噪声脑电信号波形。

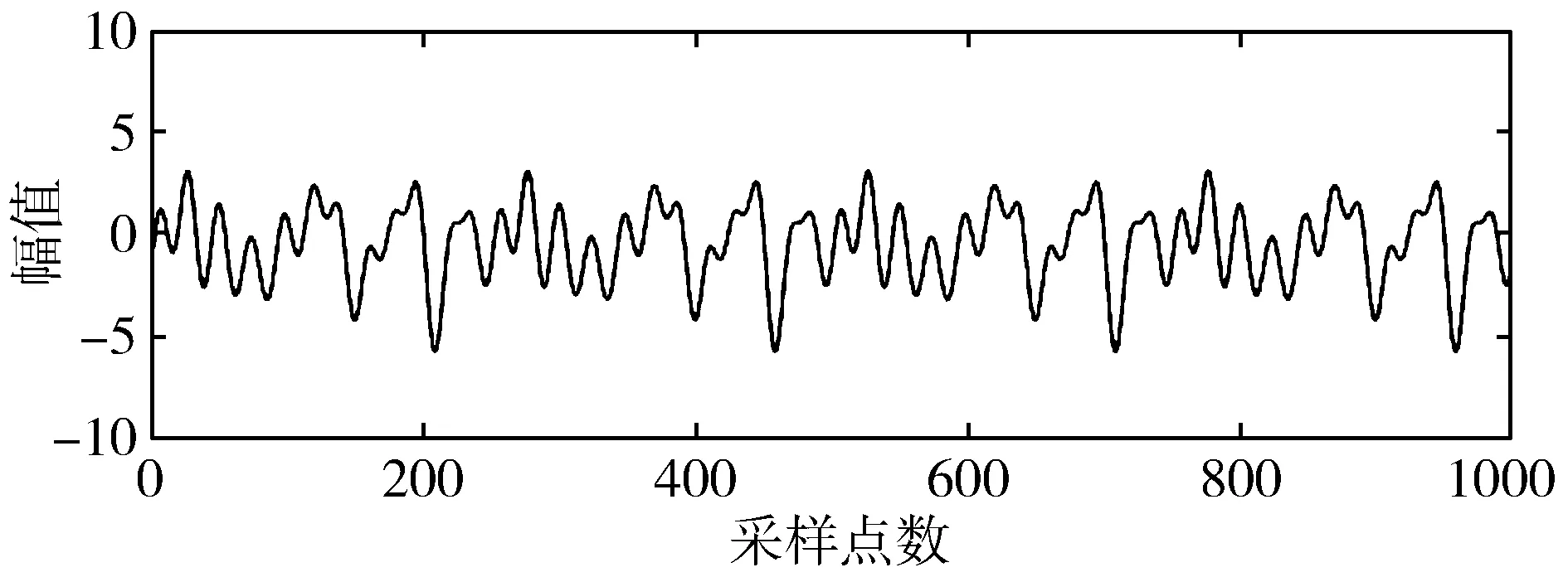
(a) 原始脑电信号

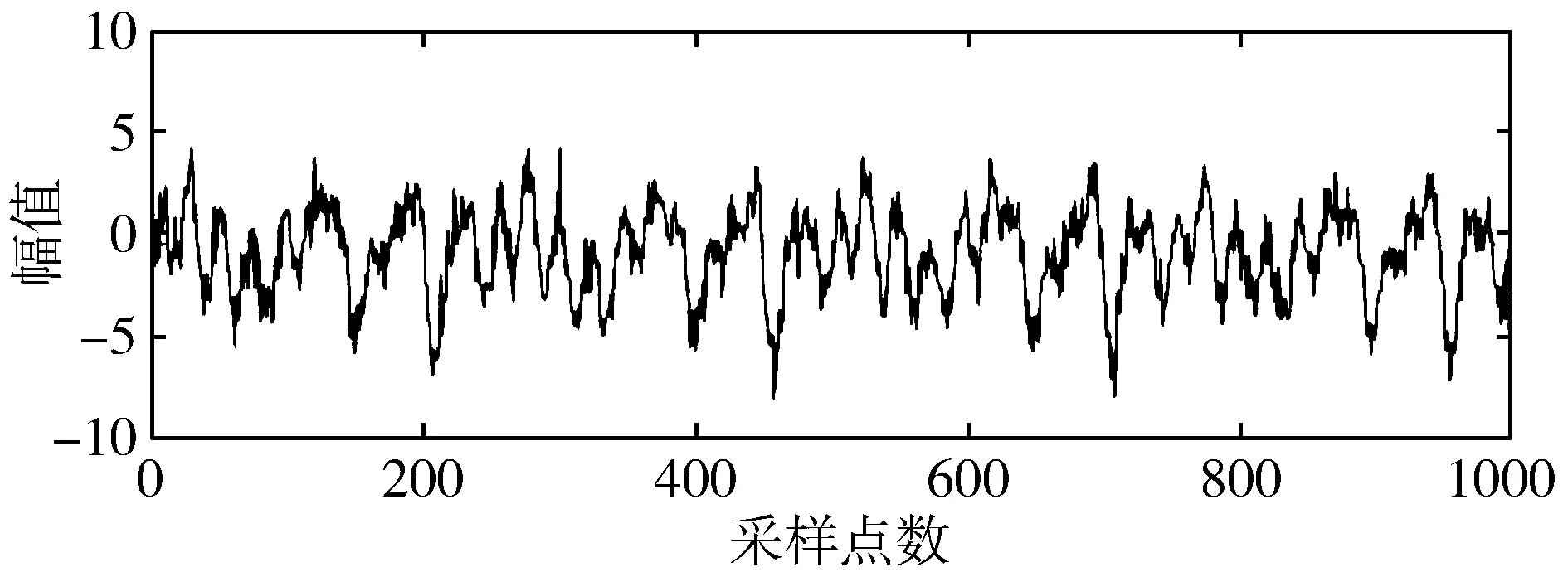
(b) 含噪脑电信号图1 仿真的原始信号和含噪信号波形图

2.2 基于CEEMD小波包降噪仿真

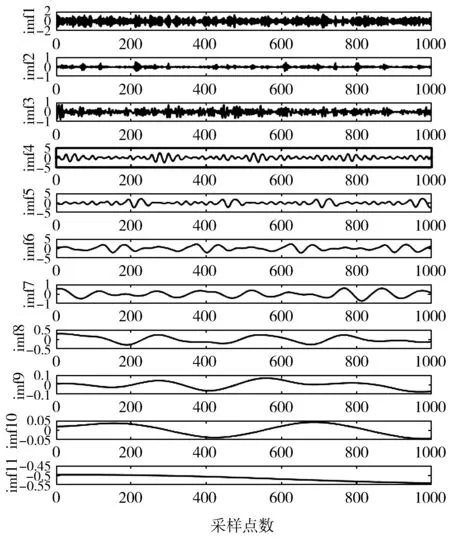
图2 CEEMD的分解结果

包含噪声的信号经过CEEMD分解后，可以得到一组频率从低到高的IMF分量。通常情况下，脑电信号主要存在于低频IMF分量中，噪声信号则大部分分布在高频IMF分量中。小波包方法为信号分析提供更加精细的方法，它在信号分析过程中对信号进行多层次划分，分别对低频带部分和高频带部分进行分解，而且可以自适应选择频段与信号频谱相对应。CEEMD的分解结果如图2所示，其降噪过程步骤如下：

1)使用CEEMD对含噪的脑电信号进行分解，得到一组IMF分量。

2)选择小波包合适的阈值函数。

3)对IMF分量按照设定阈值进行去噪。

4)对小波包降噪后的IMF分量与保留的信号IMF分量进行累加重构，获取最终降噪后的脑电信号。

5)MATLAB仿真。其波形图如图3(a)所示，频谱图如图4(a)所示。

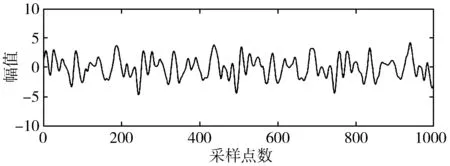
(a) CEEMD小波包降噪法

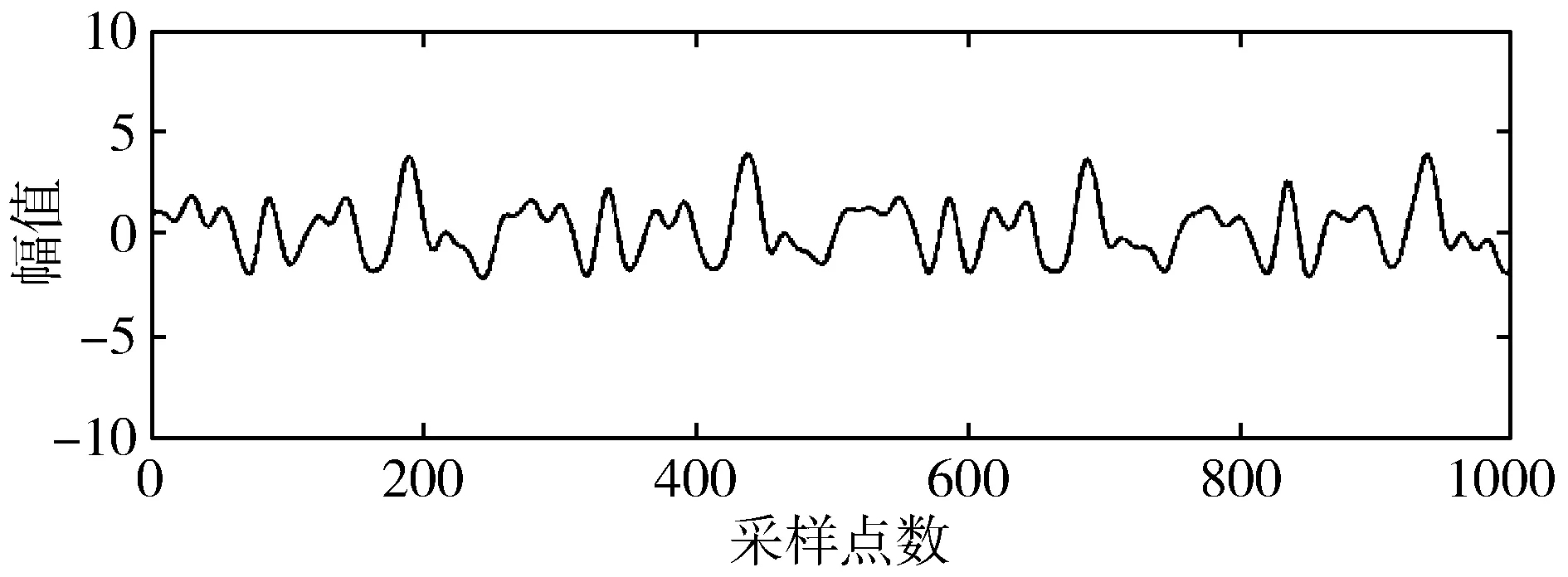
(b) 传统CEEMD降噪法

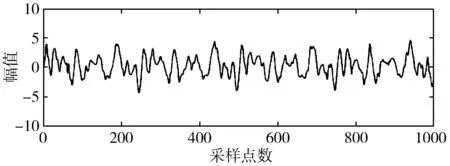
(c) 小波包降噪法图3 各种方法仿真信号降噪后的波形图

此外，为了进行比较，分别使用小波包降噪法和传统的CEEMD降噪法对仿真的含噪脑电信号进行降噪，波形图降噪结果分别如图3(b)和图3(c)所示，频谱图降噪结果分别如图4(b)和图4(c)所示。结合图3和图4可以看出，本文提出的方法不但能够基本滤除30 Hz以上的噪声，而且可以更好地保留30 Hz以内的脑电信号的细节特征，从而有效地减少了脑电信号因降噪引发的失真。

(a) CEEMD小波包降噪法

(b) 传统CEEMD降噪法

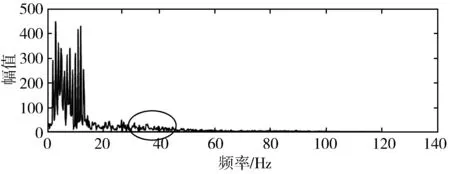
(c) 小波包降噪法图4 各种方法仿真信号降噪后的频谱图

为了进一步验证降噪效果，分别计算出每种方法的信噪比SNR与均方根误差RMSE，结果如表1所示。表1的数据显示本文提出的方法降噪后，信噪比最高，且均方根误差最小，说明在脑电信号的降噪中，CEEMD小波包降噪法性能更优。

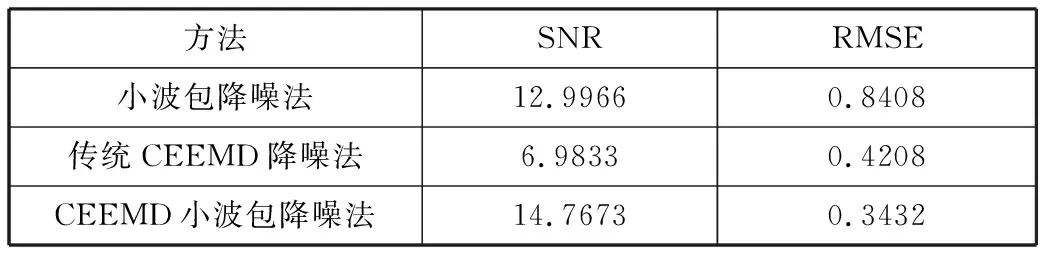
表1 3种降噪方法比较

3 结束语

由于脑电信号对噪声极其敏感，因此在预处理阶段必须对脑电信号进行降噪。本文提出的CEEMD小波包降噪法，充分发挥了CEEMD的分解特性，对分解得到的IMF分量进行分类，针对不同类别的IMF分量采取CEEMD小波包方法进行处理。仿真结果表明本文降噪方法能够有效降低噪声，为后续进行脑电信号的分析与识别奠定了良好的基础。