基于两轮自平衡小车的模糊自适应补偿算法研究
韩 帅,刘满禄,张俊俊,张 华
(西南科技大学特殊环境机器人技术四川省重点实验室,四川 绵阳 621010)
1 引言
以倒立摆为研究对象可以对控制学科中的许多典型问题进行说明,如非线性问题、鲁棒性问题、正定性问题和跟踪性问题等。此外,对倒立摆进行稳定控制对许多复杂的工程也有重大的应用价值,如火箭发射的姿态调整、直升机的飞行控制、双足机器人的稳定行走等。平衡车作为倒立摆系统最广泛、最简便的应用,具有多变量、强耦合、非线性等一系列特点,是研究相关控制算法的理想平台。
目前,国内外研究人员在平衡车控制方法方面进行了大量的研究工作,总结出了许多成熟的控制方法和控制策略,其科研成果也广泛地服务于大众。针对平衡车模糊自适应控制算法,文献[1]运用自适应的PID控制器对一级倒立摆进行了实物实验,证明其系统具有较好的瞬态性和鲁棒性;文献[2]采用模糊控制和PID控制相结合的方式,用MATLAB/Simulink对控制系统进行了仿真实验,证明了两种控制策略的有效性;窦立环建立了直线二级倒立摆系统的数学建模,将自适应模糊PID智能控制算法运用到二级倒立摆的稳定控制中,利用MATLAB对传统PID控制与自适应模糊PID控制进行对比仿真研究[3];文献[4]则提出了一种简单、易行的模糊自适应PID控制器,并对其进行了仿真实验[5]。
综合上述文献,这些控制算法和研究方法都具有其自身的一些优越性,但总的来说存在两点主要的不足:(1)仅单方面地研究自适应控制算法或模糊控制算法,未将两者结合起来[6-7];(2)部分文献尽管结合了自适应控制算法或模糊控制算法,但大都停留在了仿真阶段,未能用实物加以验证[8-9],这就使得倒立摆的模糊自适应控制算法缺少了参考价值。
基于两轮自平衡小车系统,针对外部干扰和建模不确定部分f(x)未知的问题,采用模糊系统fˆ(x)代替非线性函数f(x),实现了对平衡车的模糊自适应补偿。运用MATLAB对平衡车的角度和角速度进行了跟踪仿真实验,并在实物上对算法加以验证,对实验结果进行了较为详细的分析,结果表明:模糊自适应控制算法对自平衡小车的速度和角速度都有较好的跟踪效果,证明了该算法的有效性、实时性和稳定性。
2 系统建模
小车实物,如图1所示。整个车体由电路板、直流电机(带编码器)、电池、车轮及车身(铝型材)组成。两个带编码器的直流电机对称安装在小车底座上,分别驱动左右车轮运动,并保证轮轴线与底盘中心线重合。系统采用整合了陀螺仪和加速度传感器的六轴运动处理组件MPU6050作为姿态监测传感器,实时监测车体运动姿态,根据陀螺仪和加速度计传回的运动姿态信号,经过MPU6050数字运动处理器,可将原始数据转化为四元数输出,进一步计算出欧拉角。考虑到整个系统占用的资源,核心板采用STM32F103系列,其内部资源即可以满足系统所有需求。此外,小车装有的无线模块可使控制更为方便。

图1 两轮自平衡小车实物Fig.1 Prototype of Self-Balancing Two-Wheeled Cart
两轮自平衡小车模型示意图,如图2所示。小车模型可以简化为一级倒立摆,即车轮和轮轴为底座,车身为单摆。

图2 两轮自平衡小车模型示意图Fig.2 Sketch Map of Self-Balancing Two-Wheeled Cart model
考虑如下二阶非线性系统。


式中:f—未知的非线性函数,代表建模不确定部分或外部干扰;g—已知非线性函数;u∈Rn和y∈Rn—系统的输入和输出。设位置变量为xs,令:

式中:x1和x2—倒立摆的摆角和摆速;g—重力加速度;m—底座质量;M—车身质量;l—车身质心到电机轴长度的一半;u—控制输入。
若非线性函数f(x)已知,则可以通过直接控制u来消除其非线性部分,然后再利用线性控制理论设计合适的控制器。但实际上f(x)代表的外部干扰和建模不确定部分是不能直接测得的,因此式(3)中的控制律很难实现。此时,可采用模糊系统fˆ(x)来代替f(x),实现小车的自适应模糊补偿。实验方法为通过给小车底座施加一个正弦输入信号,通过对比分析小车角度和角速度的跟踪情况,验证模糊自适应算法的可行性。
3 模糊自适应控制器的设计与分析
3.1 模糊系统的基本理论

3.2 自适应模糊控制器的设计

3.3 稳定性分析
如前所示,将式(7)代入式(1),可得模糊控制系统的闭环动态方程为:

4 仿真实验
4.1 隶属度函数设计

4.2 仿真实验及分析
针对式(4)所述小车模型,测得实物参数,如表1所示。

表1 仿真系统相关参数Tab.1 The Related Parameters of Simulation System


表2 仿真部分初始条件Tab.2 The PartialInitial Conditions of Simulation System
仿真采用MATLAB的simulink工具箱完成,仿真时间设为30s。simulink仿真结构图,如图3所示。
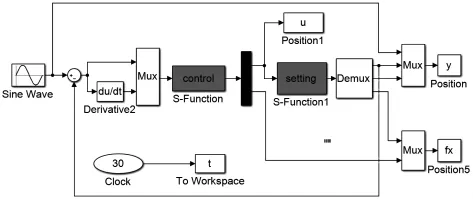
图3 自平衡小车s i m u l i n k仿真结构图F i g.3 T h e D i a g r a m o f S i m u l a t i o n S t r u c t u r e f o r t h e S e l f-B a l a n c e d C a r t
为表达方便,程序中分别用F、F1、F2表示模糊系统ξ(x)及其分母、分子。运行程序后,仿真结果,如图4所示。
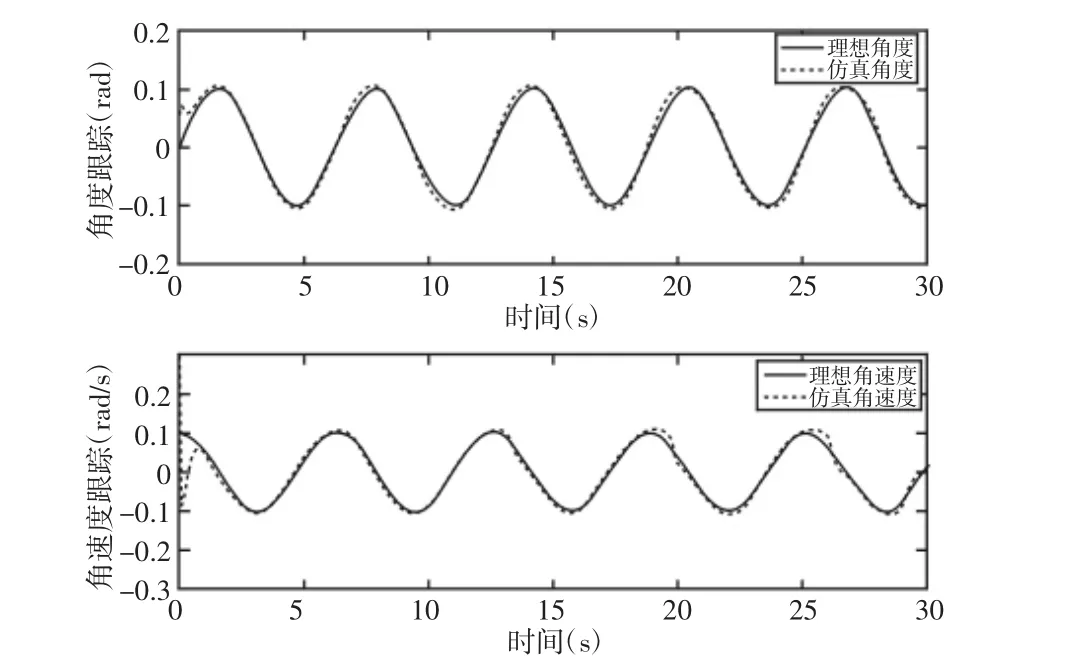
图4 角度及角速度跟踪仿真曲线Fig.4 The Tracking Curve of the Angle and Angular Velocity
分析仿真曲线可以得出,模糊自适应算法对小车角度和角速度都有较好的跟踪效果。对于角度跟踪,仿真曲线在1.5s之后即能稳定地跟踪预设函数,其最大跟踪误差为12.2%,全程平均误差为4.7%;对于角速度跟踪,仿真曲线在起始阶段有较大波动,但在1.8s之后即能稳定地跟踪预设函数,其最大跟踪误差为12.9%,全程平均误差为6.9%。
5 实物实验及相关现象分析
实验开始时小车与竖直方向保持一微小角度,各初始条件由系统给定,小车上电后,分别记录下角度、角速度在,2,…,6)时刻的值,并与预设值进行比较。角度值由安装在电机上的编码器读取,角速度值由位置指令求导后间接得出。
小车实验现象表现为:对于角度,车身在起始位置有大概1.5s的延迟,之后相对于竖直方向持续保持约为6°的左右晃动;对于角速度,车身开始有急速抖动,持续时间约为1s,之后在±6°的范围内平稳摆动。具体测量数据,如表3、表4所示。

表3 模糊自适应算法下的角度跟踪测量Tab.3 The Angle Tracking Measurement with the Algorithm Study of Fuzzy Adaptability
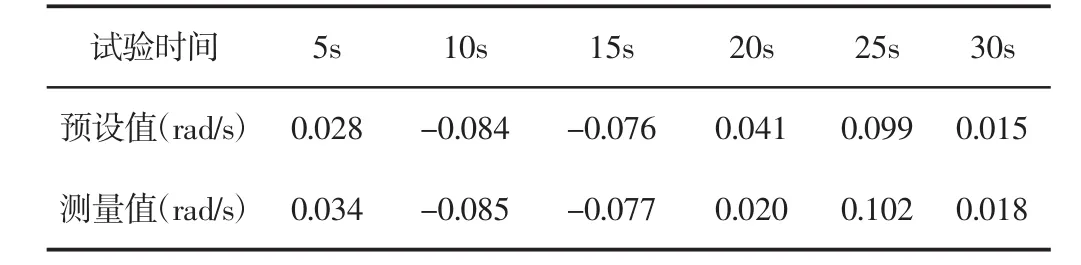
表4 模糊自适应算法下的角速度跟踪测量Tab.4 The Angular Velocity Tracking Measurement with the Algorithm Study of Fuzzy Adaptability
通过分析表3、表4可以得出,角度的平均跟踪误差为6.1%,角速度的平均跟踪误差为8%,基本符合仿真结果中的全程平均误差,跟踪效果良好,表明自平衡小车能在外部干扰和建模不确定性未知的情况下较好地实现平稳控制,也证明了模糊自适应算法的有效性和可行性。此外,在记录角速度跟踪测量数据时,发现20s时的数据存在异常,曲线上表现为较大的跳动,分析后发现此阶段有较大外力干扰,为保证数据的有效性,已舍去此组数据。
6 结论
首先针对外部干扰和建模不确定性未知的情况,从理论上证明了模糊自适应控制器的稳定性和有效性。之后通过simulink仿真、实物验证的方法,对自平衡小车的角度和角速度进行了跟踪性实验,并通过实物实验进行了验证,最后得出了“糊自适应算法能实时地对未知外部干扰和建模不确定性进行自适应模糊补偿”这一结论,对以后欠驱动系统的控制具有一定的参考价值。

