基于多无线传感器的改进数据融合算法

杨金鑫，王志明

(南京理工大学机械工程学院，江苏南京 210000)

0 引言

近年来，无线传感器技术飞速发展，利用无线传感器技术组建的多传感器数据采集系统也应用到了生活生产的很多方面，如智能家居、环境监测和智能农业[1-4]。由于无线传感器采集的数据大多是冗余的，因此近些年的研究大多集中在对数据处理的相关算法上。许可、冯丹等直接利用分批估计理论和自适应加权平均融合算法进行数据融合[5]；曹守启、刘影采用模糊集理论，根据隶属函数的隶属度剔除粗大误差，然后在分批估计的基础上，加入修正因子对温度数据进行分批自适应加权融合[6]；宋庆恒利用一种改进的拉依达准则去除异常值，然后使用加权平均算法对同类数据融合，再采用向量机模型对不同类型数据进行融合[7]；陈春玲、崔琳等通过无线传感器进行温度数据的实时采集，利用格拉布斯准则剔除异常值，然后使用自适应加权平均算法进行数据融合[8]。

在认真研究以上算法的基础上，针对其算法较复杂，需要查表等缺陷，对数据的预处理过程进行了改进，再对处理过的数据进行自适应加权融合。最后对使用格拉布斯法、改进算法和平均值法剔除数据进行融合的结果进行比较，结果表明改进算法融合结果更准确，无需查表也可以剔除异常值。

1 数据融合算法

1.1 数据预处理

在数据融合中，首先要对单个节点采集的数据进行预处理，主要是剔除粗大误差。目前的数据预处理方法种类较多，主要有拉依达准则、狄克逊准则和格拉布斯准则[9]，应用较多的是格拉布斯准则。

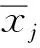
(1)

(2)

依据式(1)、式(2)的结果再通过式(3)计算格拉布斯统计量Tji，即：

(3)

规定T(n,a)为格拉布斯准则临界值，其中n为测量次数，a为显著水平，a可以取0.01或0.05，表1为摘取的部分n和a对应的T值。如果Tji>T(n,a)，则认为该数据属于异常的粗大误差值，应该剔除Tji对应的数据xji。将该数据剔除后，再重复进行上述判断，直至所有数据都满足格拉布斯准则即不存在粗大误差。然后将数据处理后得到的各组数据的标准差和平均值代入下一步的自适应加权融合算法。

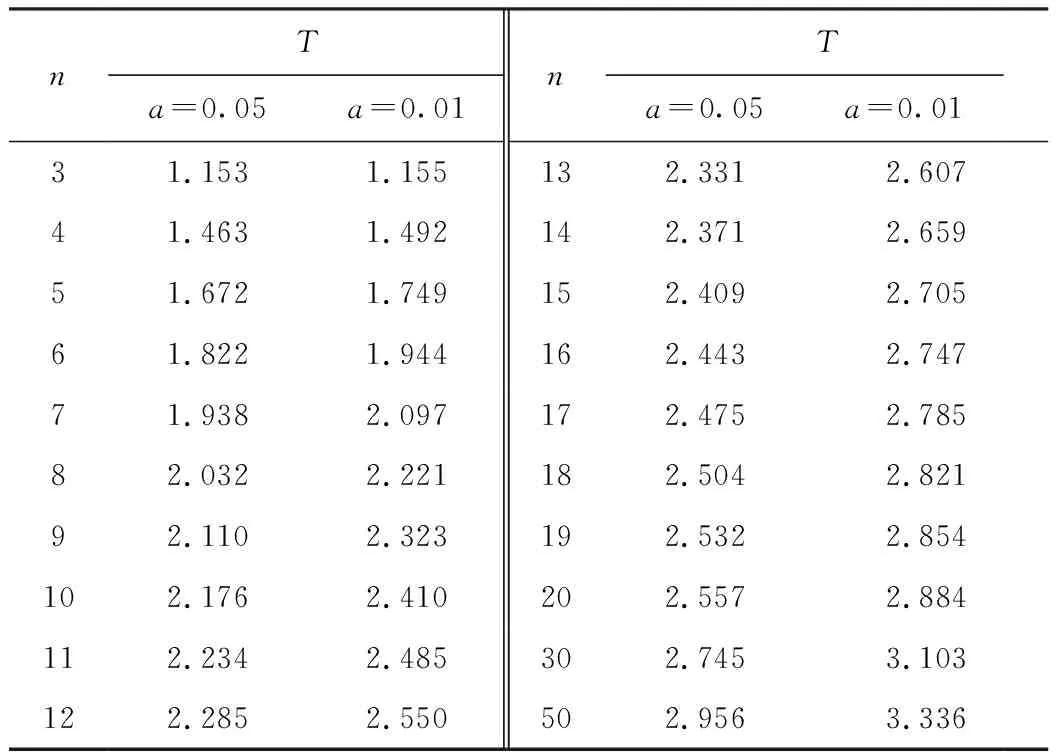
表1 格拉布斯准则临界值

1.2 自适应加权融合算法

图1 自适应加权算法模型

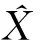
(4)

(5)

总均方误差为

(6)

由于X1，X2，X3，…，Xn彼此独立，而且为X的无偏估计。所以

E[(X-Xp)(X-Xq)=0，p≠q；p=1,2,3,…,n；q=1,2,3,…,n

(7)

因此可以化简为

(8)

从式(8)可以看出σ2为加权因子Wp的多元二次函数，为了得到最小的σ2，需要求出σ2最小时的各个Wp。问题转变为以式(5)为约束条件的多变量函数求极限问题。可以利用拉格朗日乘数法求解，最后得到:

(9)

可得σ2的最小值为

(10)

1.3 改进算法

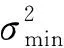
该改进算法原理如下：在对同一变量的多次测量中，如果数据较多，测量得到的数据分布可以近似为正态分布，如图2所示。在一个标准的正态分布中，其中值和平均值应该是一样的。在实际应用中，虽然不可能做到中值和平均值完全一样，但它们之间的差距不应该太大。而当一组数据的中值和平均值相差较多时，说明该组数据中有粗大误差，应当予以剔除。

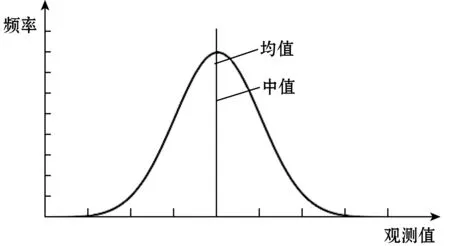
图2 正态分布示意图

设经测量得到变量xj1，xj2,…，xjn，将测得的数据按照从小到大进行排序得到集合U={xmin,…,xmax}，将集合U中的最大值xmax去除得到数组A，将集合U中的最小值xmin去除得到数组B。

A∈U,B∈U

求取新得到的2个集合A和B中的数据的平均值和中值，得到Aave，Amed，Bave，Bmed，然后对2个新的数组的平均值和中值进行求差：

A-=|Aave-Amed|

B-=|Bave-Bmed|

2 结果及分析

2.1 数据来源

由于主要是对算法计算结果的验证和比较，因此这里引用了文献[5]的某时段待融合温度数据来进行处理，进而实现算法的验证和比较，引用数据见表2。

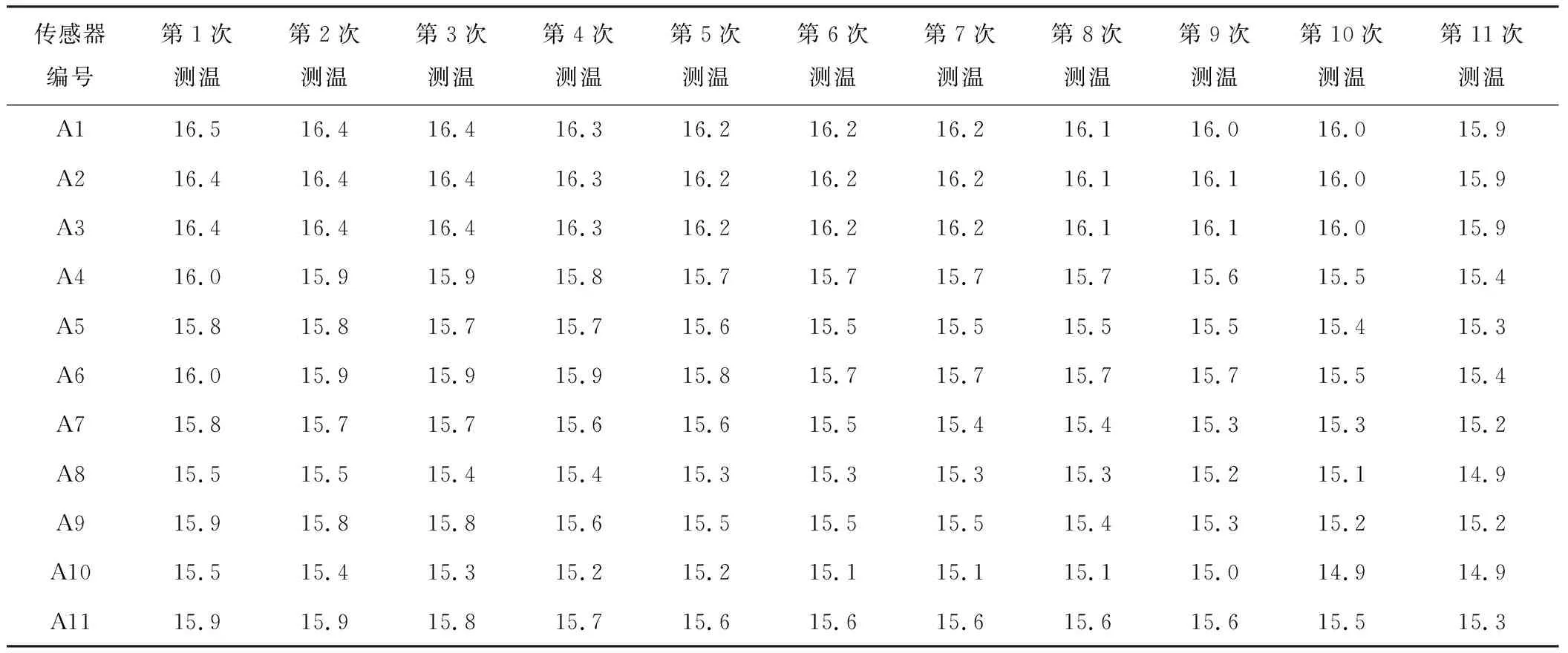
表2 某时段待融合温度数据[5] ℃

该组数据中共有11组数据，每组数据有11个传感器的测量值，这里选取6组数据A1、A3、A5、A7、A9、A11进行算法的验证。在A1中引入了2个同侧误差17.1 ℃、17.0 ℃，在A7中引入了一个误差14.3 ℃，算法验证所使用的数据如表3所示。

表3 算法验证所用数据[5] ℃

2.2 结果分析

由于标准差σ代表一组数据集的离散程度，所以以下的分析以σ作为评价标准。

表4为格拉布斯法对A1组数据的处理过程，在对A1组数据进行预处理的过程中可以看出：格拉布斯法不能发现引入的2个同侧误差，即出现同侧异常值屏蔽效应。

最终预处理的结果是：X1=16.31 ℃，σ1=0.375 3 ℃。

而使用改进的算法可以剔除17.1 ℃这个引入误差，最终预处理的结果是：X1=16.23 ℃，σ1=0.293 4 ℃。

可以看出，使用改进的方法能够对格拉布斯法的同侧异常值屏蔽效应进行部分纠正，从而使结果更精准。

接着使用完整的算法进行融合得到最终结果，这里引用了不对数据进行预处理和使用格拉布斯法进行数据预处理来与改进算法进行对比，表5、表6和表7分别为平均值处理、格拉布斯准则处理和改进算法处理后的融合结果。

表4 格拉布斯法对A1组数据的处理过程

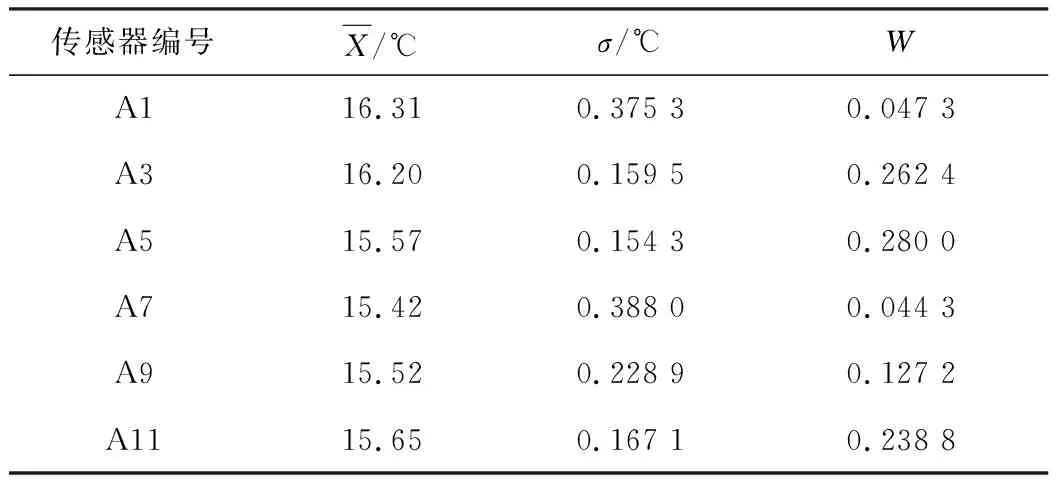
表5 平均值处理后融合结果

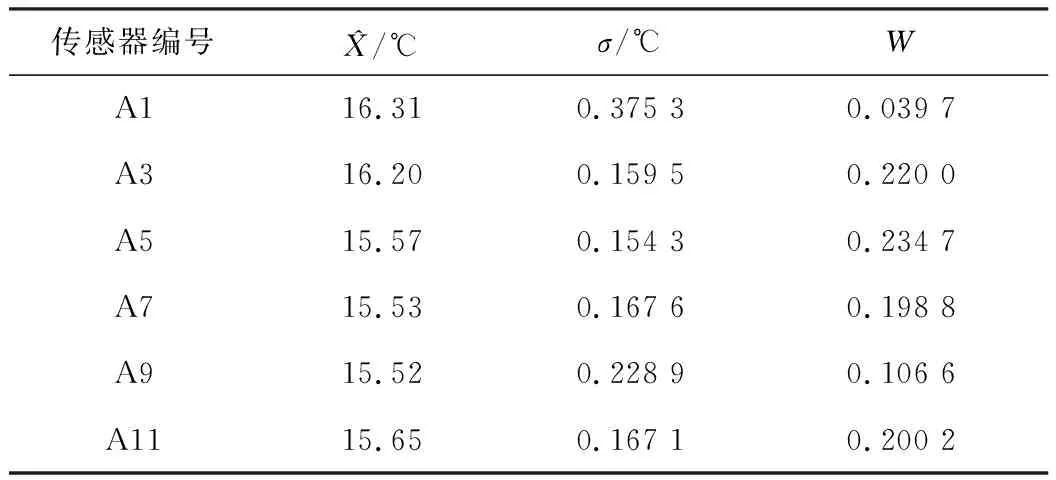
表6 格拉布斯准则处理后融合结果

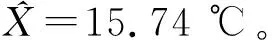
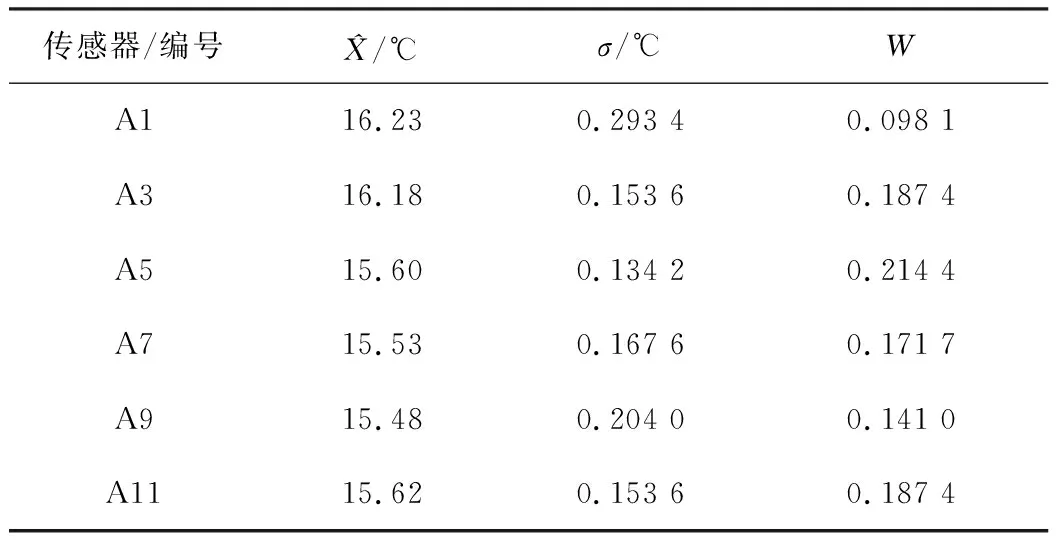
表7 改进算法处理后融合结果

从所得结果中可以看出各种预处理算法的优越性：改进算法>格拉布斯法>不进行预处理，从A1组数据的处理结果可以看出改进的算法可以有效抑制同侧屏蔽效应，从A7组数据的处理结果可以看出改进的算法和格拉布斯法同样能够有效剔除粗大误差，提高处理结果的准确性。从整体来看，改进算法能够同时剔除同侧误差和粗大误差，相对其他处理方式能够得到更符合要求的结果。

无线传感器所用芯片内存较小，如果使用格拉布斯法进行处理，需要在内存中储存该临界值表，这样会占据较大的内存空间。而在无线传感器芯片中还需要存储路由协议表、历史数据等多种必要信息，如果再加上格拉布斯临界值表，会造成内存紧张。改进算法无需查表，可以最大程度地减少因为算法需要对内存空间的占用。

3 结束语

提出了一种对当前数据融合算法进行改进的新算法，主要在数据预处理阶段进行数据加工，然后使用自适应加权融合算法进行数据融合。从分析结果可以看出：

(1)改进算法主要针对数据的预处理阶段进行了改进，从对实验数据进行处理的结果可以看出，改进算法相对格拉布斯法进行预处理和不进行预处理两种方式有更好的融合结果。

(2)改进算法无需查表，相对格拉布斯法和狄克逊法均需要查表相比，可以节省一部分内存空间，提升系统的其他方面的性能。